Cosine 余弦相似度并行计算的数学原理与Python实现

背景

Cosine 我在LLM与RAG系列课程已经讲了很多次了，这里不在熬述，它在LLM分析中，尤其是在语义相似度的计算中至关重要，在dot attention机制中，也会看到他的身影。这里讲的是纯数学上的运算与python是如何运用相关库进行并行计算的原理及实践。完全掌握了他，在看vector db 里面的语义相似度，你可能会豁然开朗。实现总是如此的优雅。

Cosine的定义，两个向量(A, B), 他们的余弦相似度为：

Cosine(A,B) = (A * B)  /  (len(A) * len (B))

其实就是距离在M维坐标系的分别投影，前面也说了很多次了，不明白可以参看LLM与RAG系列课程。下面举个例子，很简单的初中数学，两个二维向量A，B，如果他们维度所包含的分量都相等，那么Cosine = 1, 很好理解：A（x, y）, B(x, y)

A  *  B =  （x, y） * （x, y）= x^2 + y^2

len(A) = sqrt(x^2 + y^2)

len(B) = sqrt(x^2 + y^2)

最后答案就是 Cosine（A， B） = 1

如果是N维向量，很显然，相同。

Cosine(A,B) = (A * B)  /  (len(A) * len (B))

问题来了，我如果给你很多个A，很多个B，要你求所有A，B之间的 Cosine，要怎么处理？最笨的办法就是写个  def cosine(A,B)   return  (A * B)  /  (len(A) * len (B)),  然后写一个二层for循环，case by case，这样的代码交给CPU 做AI，肯定是不合适的。怎么优化呢？那就是线性代数的魅力来了，Matrix 运算。我们看看怎么做。

向量内积

向量内积，不要总想着二，三维，那是初中，高中的东西。在LLM的世界，高维向量普遍存在，在Choma vector db 提供的基础 embedding中，嵌入向量为 384 维度。那还算比较小的。大一点的上千维度都很正常。向量的内积，很简单，就是M维向量的M维度分别相乘后相加，放到Matrix 的指定位置就对了，python 实现更简单，就是 A dot B， 一个 dot 解决了（M , N）与 (N , J)维度的matrix 乘法。有点线性代数功底的都知道：（M , N）* (N , J) = (M, J)。 可是问题来了，在LLM的世界中，因为嵌入向量都是 M维，表达方式都是 （M , N）, (J, N) 这种是没办法做 向量内积的，怎么办？很简单，转置一下，（M , N）* (J， N)T = (M, J)。 以前总觉得现线性代数没啥用，现在看到了它的魅力，你要用它的时，如果你概念基础扎实，马上就上手了。讲到了这里，看下 python 的例子：

arr1 = np.array([[1, 2, 3], [2, 3, 5], [1, 4, 3]])
arr2 = np.array([[4, 5, 6], [1, 2, 3]])
print(np.dot(X, Y.T))

非常简洁的代码，看下输出：

nice。不要小看他，它相当于是将将arr1的三个二维向量与arr2的两个二维向量在 O(0)同时完成了计算结果。而且 python 的 numpy 底层是经过 compiler 优化的，性能还是非常出色。

向量外积 

是一个线性代数中的概念，指的是两个向量的张量积（tensor product），其结果是一个矩阵。

具体来说，假设 X_norm 是一个形状为 (m,) 的一维数组（向量），而 Y_norm 是一个形状为 (n,) 的一维数组（向量）。那么，np.outer(X_norm, Y_norm) 将返回一个形状为 (m, n) 的二维数组（矩阵），其中第 i 行第 j 列的元素是 X_norm[i] 和 Y_norm[j] 的乘积。

用数学符号表示，如果 X_norm = [x_1, x_2, ..., x_m] 和 Y_norm = [y_1, y_2, ..., y_n]，那么(X_norm, Y_norm)的外积 将产生一个矩阵，其元素为：

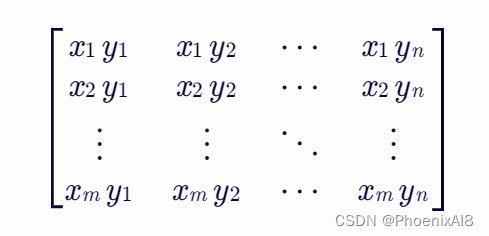
python 代码实现：

import numpy as np 
X_norm = np.array([1, 2]) 
Y_norm = np.array([3, 4, 5]) 

result = np.outer(X_norm, Y_norm)
print(result)

向量的长度

就是 2-范数或称为欧几里得范数，各维度平方相加开根号。

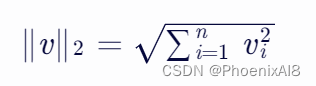
就是上面说的 len

p.linalg.norm 是 NumPy 中的一个函数，用于计算向量或矩阵的范数。具体来说，np.linalg.norm(X, axis=1) 是在 NumPy 数组 X 上沿着指定的轴（在这里是 axis=1）计算向量的 2-范数（或称为欧几里得范数）。

假设 X 是一个形状为 (m, n) 的二维数组（或矩阵），其中 m 是行数，n 是列数。那么 np.linalg.norm(X, axis=1) 会返回一个长度为 m 的一维数组，其中每个元素是 X 中对应行的 2-范数。

还是上面那个例子，看下代码与运行结果：

arr1 = np.array([[1, 2, 3], [2, 3, 5], [1, 4, 3]])
arr2 = np.array([[4, 5, 6], [1, 2, 3]])

X_norm = np.linalg.norm(arr1, axis=1)
Y_norm = np.linalg.norm(arr2, axis=1)

发现维度没变，还是之前的，shape 都相同。只是做了平方求和开根号的处理。

LLM中的应用

到了这里，我们发现，如果我们使用：

X = np.array([[1, 2, 3], [2, 3, 5], [1, 4, 3]])
Y = np.array([[4, 5, 6], [1, 2, 3]])
X_norm = np.linalg.norm(arr1, axis=1)
Y_norm = np.linalg.norm(arr2, axis=1)
similarity = np.dot(X, Y.T) / np.outer(X_norm, Y_norm)

他就是关于X的每个二维的分量与Y的每个二维分量之间的 Cosine。因为它同时完成了对应每个位置的 (A * B)  /  (len(A) * len (B))

我们看看结果：

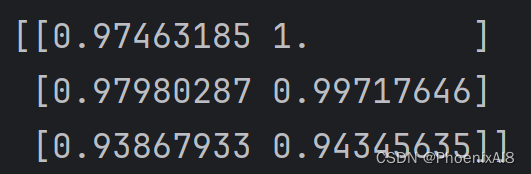
数学含义也很明确，比如在 X的 [1,2,3] 对 Y的 [1,2,3]时， Cosine = 1，非常完美的三行代码。不要看不起它，他在vector db 中起着举足轻重的作用。今天介绍到这里，如果你对LLM感兴趣，可以读下我的其他专栏，同步更新中。