[NOI2019]序列

StaroForgin

已于 2023-07-11 11:03:44 修改

阅读量190

点赞数 2

分类专栏： ------贪心------ # 网络流文章标签：算法贪心算法

于 2022-07-19 22:56:19 首次发布

本文链接：https://blog.csdn.net/tan_tan_tann/article/details/125882052

版权

------贪心------ 同时被 2 个专栏收录

64 篇文章 0 订阅

订阅专栏

网络流

20 篇文章 0 订阅

订阅专栏

序列

题解

~~非要我评价的话我只能说*b题就这样的，网络流就网络流嘛，还非得手动模拟，就是屑。~~

首先，我们应该比较容易地构建出它的网络流模型。
至少有 $L$ 个选择的下标相同显然可以转化成最多选择 $K - L$ 对下标不同。
我们的网络流相当于构建一个二分图，图上所有 $a_i$ 都可以随便和它对应的 $b_i$ 相匹配，而不同的匹配最多只有 $K - L$ 个，连出来是长这样的：
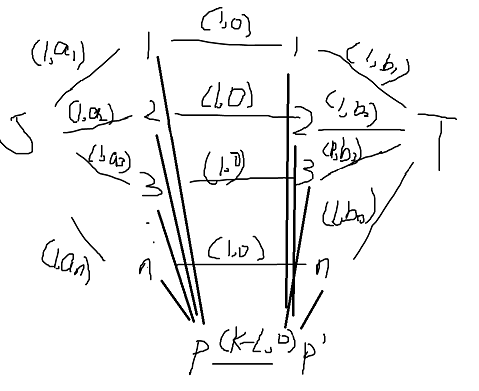
在这里插入图片描述
我们要去求的是这个图的最大费用最大流~~图画得貌似有点丑~~，显然直接把边权倒过来跑肯定是跑不过 $n\leqslant 2\times 10^5$ 的。
对于这种简单分层图的费用流一种比较经典的方法是利用贪心来模拟网络流。
显然，这种退流也是比较容易整到可撤销贪心上的。
我们先观察这张图，显然，那 $K - L$ 条边的选择余地是最大的，所以说如果我们还没选满的话就可以直接把 $A$ 现在剩下的最大的一个和 $B$ 现在剩下的最大的一个给拿进去。
否则的话我们就有两种选择，一是将一对没有被选择的 $a_i,b_i)$ 选上，一是撤销原先选上的一堆 $a_i,b_j)$ ，变成 $a_i,b_i)+(a_x,b_y)$ ，这样都不会影响我们拿 $K - L$ 条边的选择。
我们可以直接把两种的改变量记录下来，比较哪种改变量更大就选哪种。

当然，直接维护这些可能不太好搞。
我们可以维护 $a$ 选在那 $K - L$ 条边中的集合， $b$ 选在那 $K - L$ 条边中的集合， $a$ 没有被选的集合， $b$ 没有被选的集合。
显然，一种改变量就是后面两个集合的交集中和最大的那一堆，一种改变量就是把第一个集合中 $i$ 中最大的 $b_i$ 加上，减去第二个集合中最小的 $b_i$ ，在把后面两个集合中最大的拿出来。
这些都可以直接用优先队列维护。
大体思路就是这样的，不过还得注意一些细节。
比如说我们维护的加入那 $K - L$ 条边的集合是不能有交集的，否则它们就不会贡献在这里了。
也就是说我们后面加进来的点与它有交集的话，可以直接把它们都删掉。
这当然会导致后面又可以随便选边了，当然要记录一下。
另外就是它可能上面 $a_i,b_j)->(a_i,b_i)+(a_x,b_y)$ 中 $y$ 也是可能为 $j$ 的，要特判一下。
当然，也可以是 $a_i,b_j)->(a_j,b_j)+(a_x,b_y)$ 的，对称的嘛。

所以只需要维护堆就行了，每次都会多选一对点，最多只会选 $K$ 次。
总时间复杂度 $O\left(\sum n\log n\right)$ 。

源码

~~维护 $7$ 个堆也可以过。~~

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<LL,int> pii;
#define MAXN 200005
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lowbit(x) (x&-x)
const int mo=998244353;
const int inv2=5e8+4;
const int jzm=2333;
const int zero=15;
const LL INF=0x3f3f3f3f3f3f3f3f;
const double Pi=acos(-1.0);
const double eps=1e-9;
const int lim=1000000;
const int orG=3,ivG=332748118;
const int n1=500;
const int M=MAXN/n1+5,N=n1+5;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
    _T f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
    x*=f;
}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int T,n,K,L,a[MAXN],b[MAXN];LL ans;
bool visa[MAXN],visb[MAXN];
priority_queue<pii>A1,B1,A2,B2,A3,B3,C;
int main(){
    read(T);
    while(T--){
        while(!A1.empty())A1.pop();while(!B1.empty())B1.pop();
        while(!A2.empty())A2.pop();while(!B2.empty())B2.pop();
        while(!A3.empty())A3.pop();while(!B3.empty())B3.pop();
        while(!C.empty())C.pop();
        read(n);read(K);read(L);int num=0;
        for(int i=1;i<=n;i++)read(a[i]);
        for(int i=1;i<=n;i++)read(b[i]);
        for(int i=1;i<=n;i++)
            A1.push(mkpr(a[i],i)),
            B1.push(mkpr(b[i],i)),
            C.push(mkpr(a[i]+b[i],i));
        for(int i=1;i<=K;i++){
            while(!A1.empty()&&visa[A1.top().sec])A1.pop();
            while(!B1.empty()&&visb[B1.top().sec])B1.pop();
            while(!A2.empty()&&!visa[A2.top().sec])A2.pop();
            while(!B2.empty()&&!visb[B2.top().sec])B2.pop();
            while(!A3.empty()&&!visa[A3.top().sec])A3.pop();
            while(!B3.empty()&&!visb[B3.top().sec])B3.pop();
            while(!C.empty()&&(visa[C.top().sec]||visb[C.top().sec]))C.pop();
            if(num<K-L){
                pii ta=A1.top(),tb=B1.top();A1.pop();B1.pop();ans+=ta.fir+tb.fir;
                visa[ta.sec]=visb[tb.sec]=1;if(ta.sec==tb.sec)continue;
                if(!visa[tb.sec]&&!visb[ta.sec])num++;
                if(visb[ta.sec]&&visa[tb.sec])num--;
                if(visb[ta.sec])visb[ta.sec]=0;else A2.push(mkpr(b[ta.sec],ta.sec)),A3.push(mkpr(-ta.fir,ta.sec));
                if(visa[tb.sec])visa[tb.sec]=0;else B2.push(mkpr(a[tb.sec],tb.sec)),B3.push(mkpr(-tb.fir,tb.sec));
            }
            else{
                LL tmpa=-INF,tmpb=-INF,tmpc=-INF,tmpd=-INF,tmpe=-INF;
                if(!C.empty())tmpc=C.top().fir;
                if(!A2.empty()&&!B3.empty())tmpa=A2.top().fir+B3.top().fir+A1.top().fir+B1.top().fir;
                if(!A3.empty()&&!B2.empty())tmpb=A3.top().fir+B2.top().fir+A1.top().fir+B1.top().fir;
                if(!A2.empty())tmpd=A2.top().fir+A1.top().fir;
                if(!B2.empty())tmpe=B2.top().fir+B1.top().fir;
                LL td=max(max(tmpa,tmpb),max(tmpc,max(tmpd,tmpe)));ans+=td;
                if(tmpc==td){pii t=C.top();C.pop();visa[t.sec]=visb[t.sec]=1;}
                else if(tmpa==td){
                    pii t1=A2.top(),t2=B3.top();A2.pop();B3.pop();
                    pii ta=A1.top(),tb=B1.top();A1.pop();B1.pop();
                    visa[t1.sec]=visb[t2.sec]=0;visb[t1.sec]=1;B1.push(mkpr(b[t2.sec],t2.sec));
                    if(!visa[t2.sec])C.push(mkpr(a[t2.sec]+b[t2.sec],t2.sec));visa[ta.sec]=visb[tb.sec]=1;
                    if(visb[ta.sec])visb[ta.sec]=0,num--;else A2.push(mkpr(b[ta.sec],ta.sec)),A3.push(mkpr(-ta.fir,ta.sec));
                    if(visa[tb.sec])visa[tb.sec]=0,num--;else B2.push(mkpr(a[tb.sec],tb.sec)),B3.push(mkpr(-tb.fir,tb.sec));
                }
                else if(tmpb==td){
                    pii t1=A3.top(),t2=B2.top();A3.pop();B2.pop();
                    pii ta=A1.top(),tb=B1.top();A1.pop();B1.pop();
                    visa[t1.sec]=visb[t2.sec]=0;visa[t2.sec]=1;A1.push(mkpr(a[t1.sec],t1.sec));
                    if(!visb[t1.sec])C.push(mkpr(a[t1.sec]+b[t1.sec],t1.sec));visa[ta.sec]=visb[tb.sec]=1;
                    if(visb[ta.sec])visb[ta.sec]=0,num--;else A2.push(mkpr(b[ta.sec],ta.sec)),A3.push(mkpr(-ta.fir,ta.sec));
                    if(visa[tb.sec])visa[tb.sec]=0,num--;else B2.push(mkpr(a[tb.sec],tb.sec)),B3.push(mkpr(-tb.fir,tb.sec));
                }
                else if(tmpd==td){
                    pii t1=A2.top(),t2=A1.top();A2.pop();A1.pop();
                    visa[t1.sec]=0;visb[t1.sec]=visa[t2.sec]=1;
                    if(visb[t2.sec])visb[t2.sec]=0,num--;
                    else A2.push(mkpr(b[t2.sec],t2.sec)),A3.push(mkpr(-t2.fir,t2.sec));
                }
                else if(tmpe==td){
                    pii t1=B2.top(),t2=B1.top();B2.pop();B1.pop();
                    visb[t1.sec]=0;visa[t1.sec]=visb[t2.sec]=1;
                    if(visa[t2.sec])visa[t2.sec]=0,num--;
                    else B2.push(mkpr(a[t2.sec],t2.sec)),B3.push(mkpr(-t2.fir,t2.sec));
                }
            }
        }
        printf("%lld\n",ans);ans=0;
        for(int i=1;i<=n;i++)visa[i]=visb[i]=0;
    }
    return 0;
}