2.4 关系代数

夏驰和徐策

已于 2023-12-04 17:25:18 修改

阅读量564

点赞数 2

分类专栏：数据库系统概论文章标签：数据库 sql

于 2023-10-09 00:00:40 首次发布

本文链接：https://blog.csdn.net/tang7mj/article/details/133692133

版权

数据库系统概论专栏收录该内容

54 篇文章

订阅专栏

思维导图：

前言：

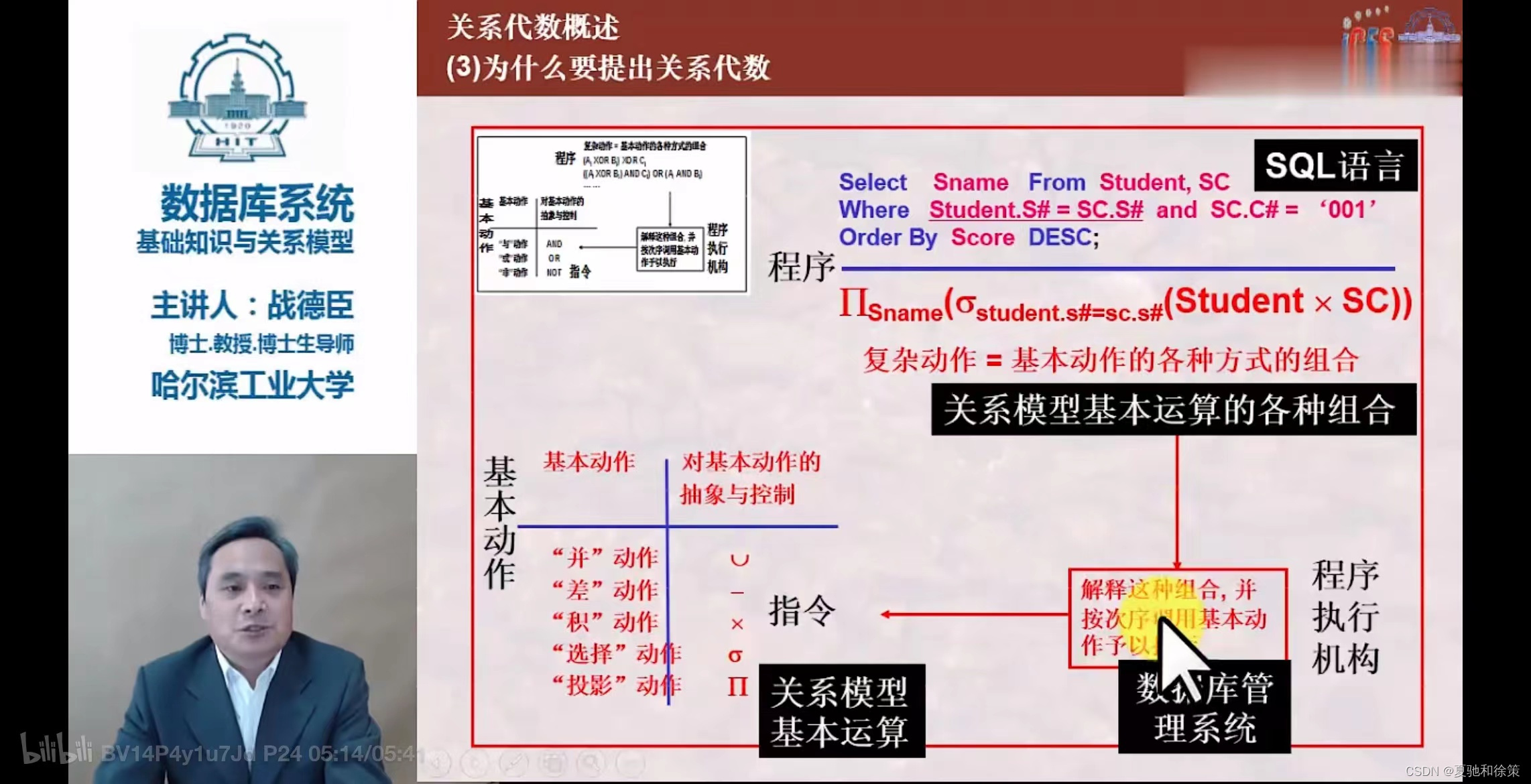
2.4 关系代数

定义与概念

关系代数（Relational Algebra） 是一种用于数据库查询和理论分析的抽象语言。
它通过对关系（即表）的运算来表达数据库的查询操作。

基本要素

运算对象：关系代数的基本操作对象是关系，即数据库中的表。
运算符：用于对关系进行操作的符号。
运算结果：操作的结果，也是一个关系（表）。

主要运算符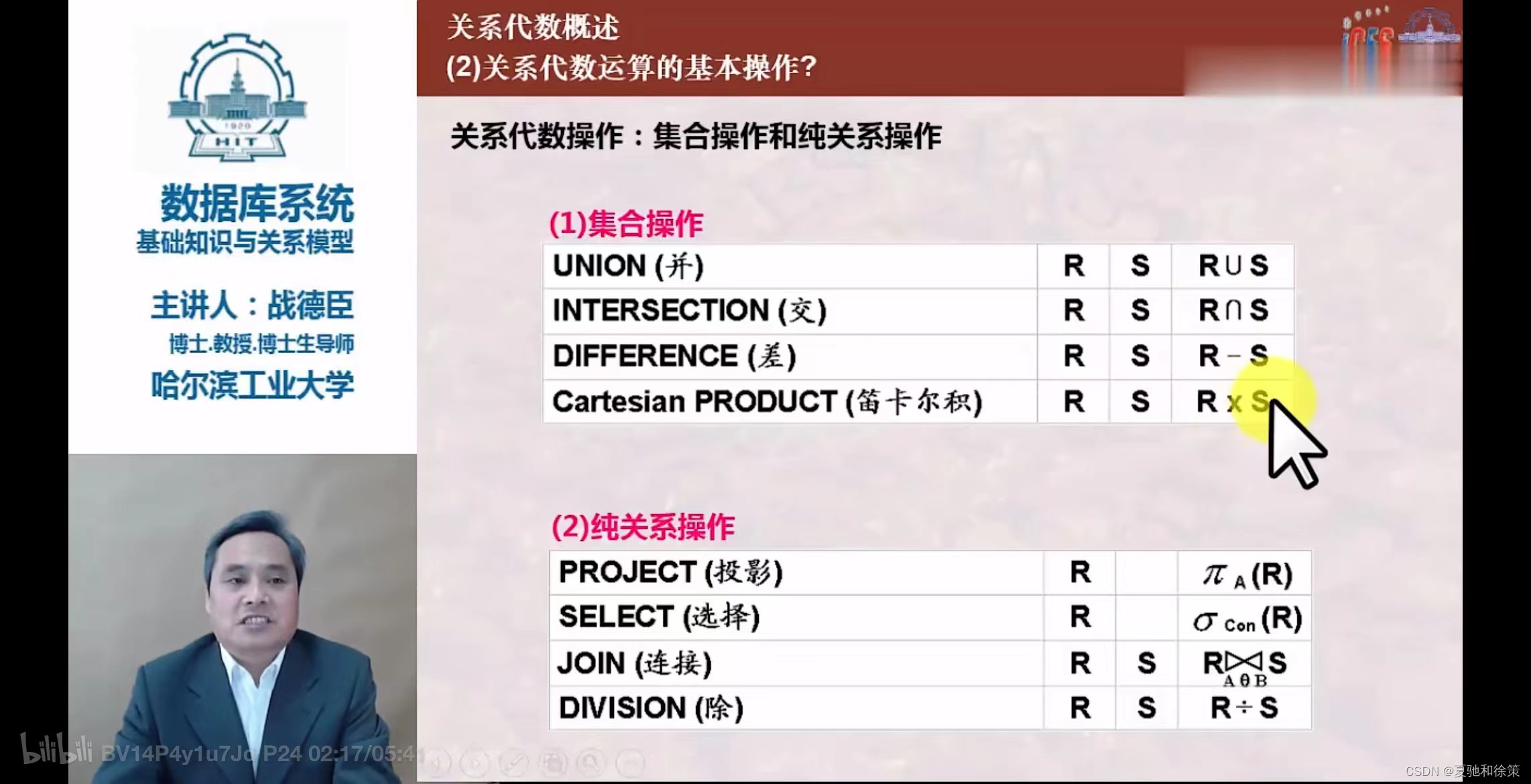

集合运算符
- ∪ (并)：合并两个关系中的元组。
- − (差)：从一个关系中去除与另一个关系相同的元组。
- ∩ (交)：找出两个关系中共有的元组。
- × (笛卡尔积)：组合两个关系中的元组。
专门的关系运算符
- σ (选择)：根据特定条件选择元组。
- π (投影)：选择某些特定的列。
- ⋈ (连接)：根据共有属性连接两个关系的元组。
- ÷ (除)：一种专门的运算，用于某些特定的查询。

特点

运算的多样性：关系代数包括集合运算和专门的关系运算。
操作角度：集合运算着重于关系的“水平”方向（即行），而专门的关系运算则涉及到“垂直”方向（即列）的操作。
辅助运算符：比较运算符和逻辑运算符也用于辅助进行关系运算。

2.4.1 传统的集合运算

概述

传统的集合运算 包括并（Union）、差（Except）、交（Intersection）、笛卡尔积（Cartesian Product）这四种基本运算。
这些运算是二元运算，即它们操作两个运算对象。

运算定义

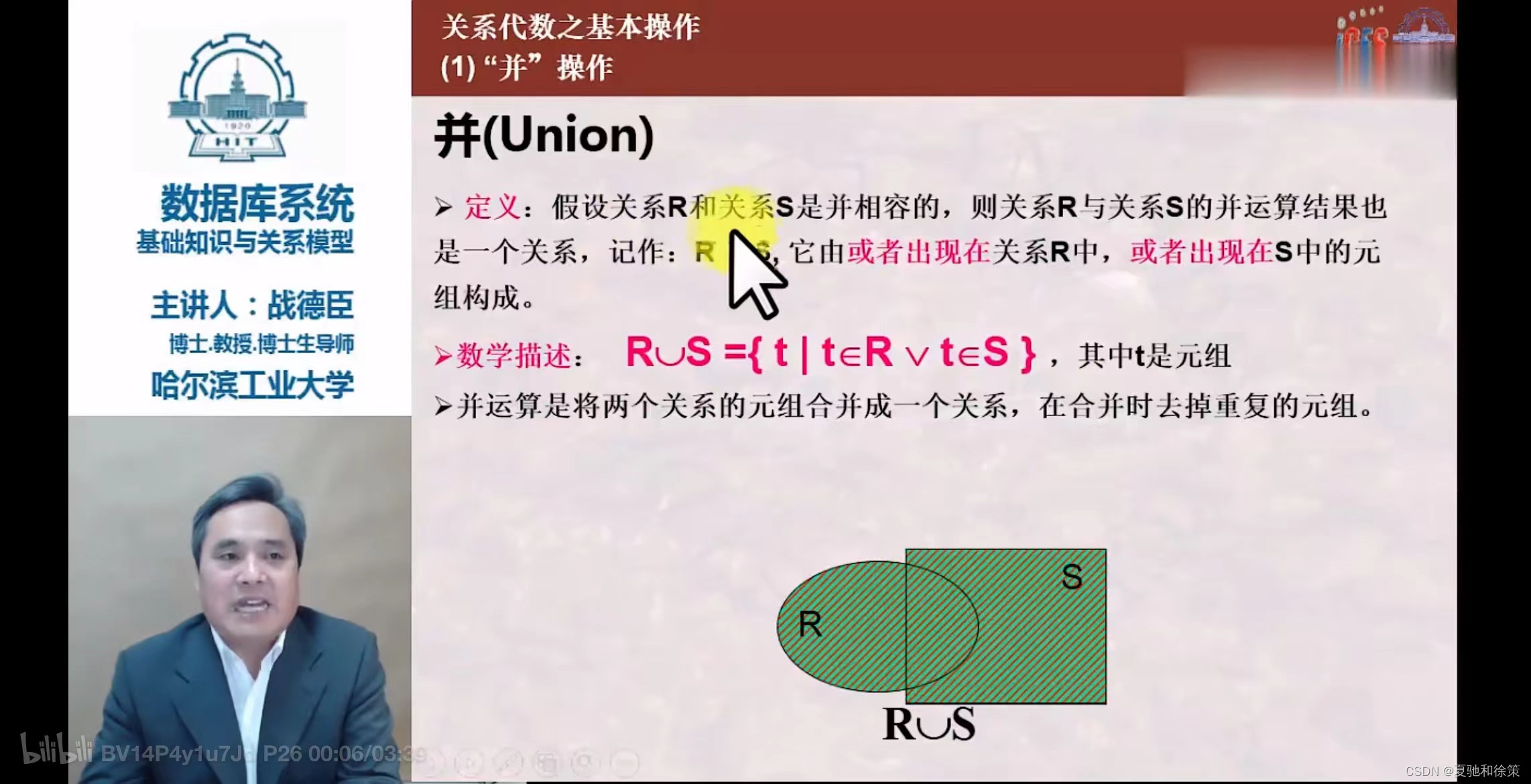
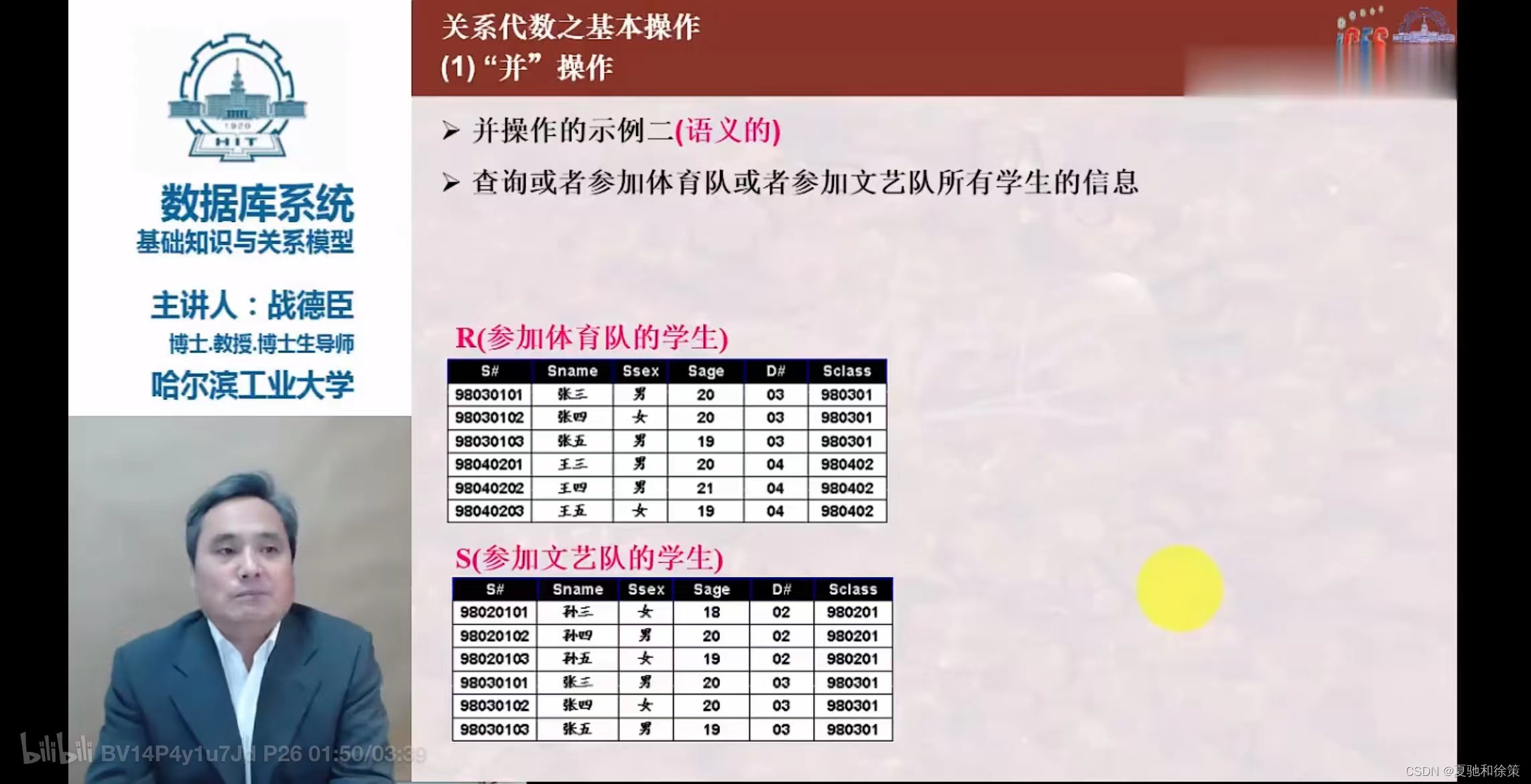
并 (Union)
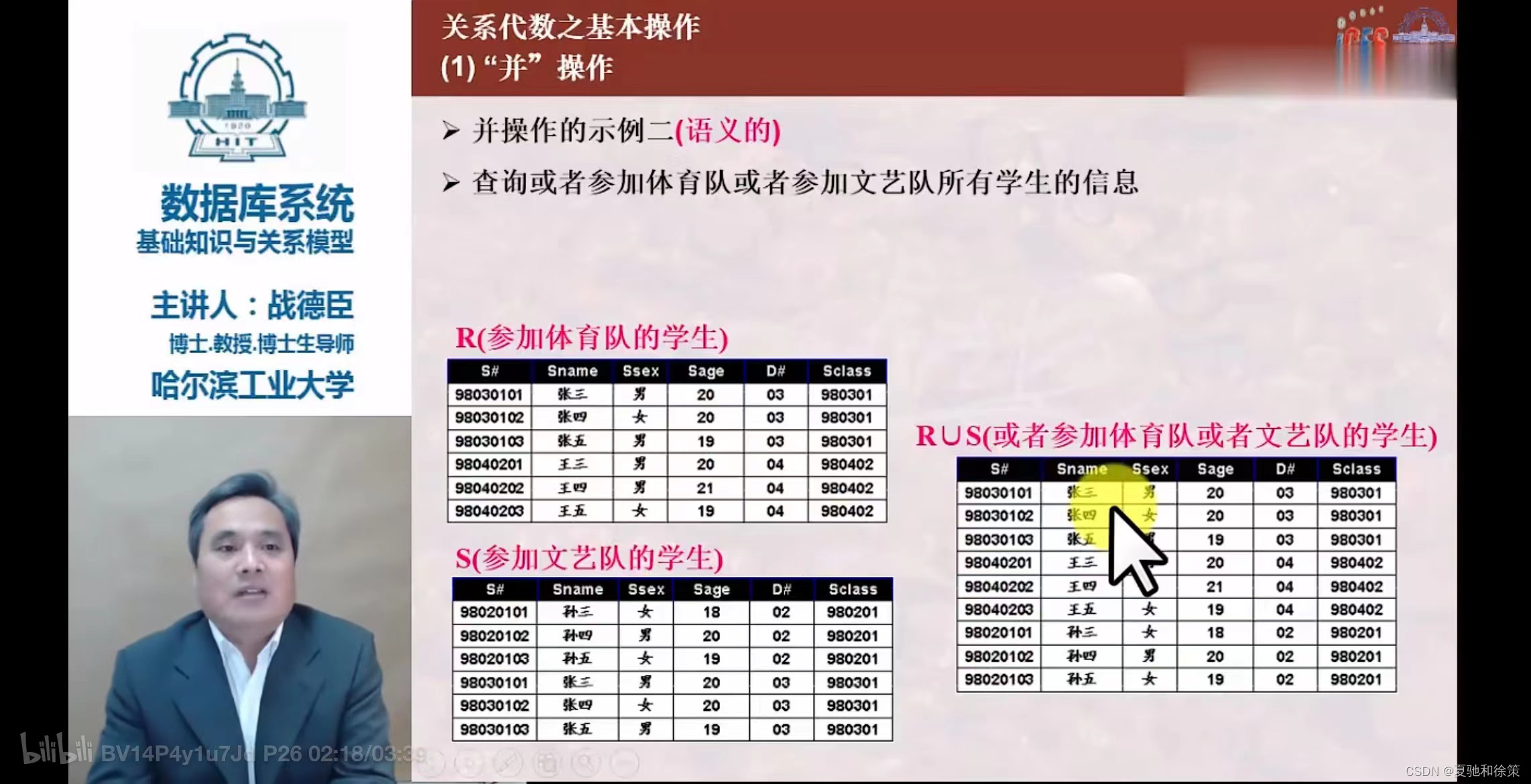
- 符号：R ∪ S
- 条件：关系R和S具有相同的目（属性数）n。
- 结果：包含属于R或属于S的所有元组的n目关系。
差 (Except)
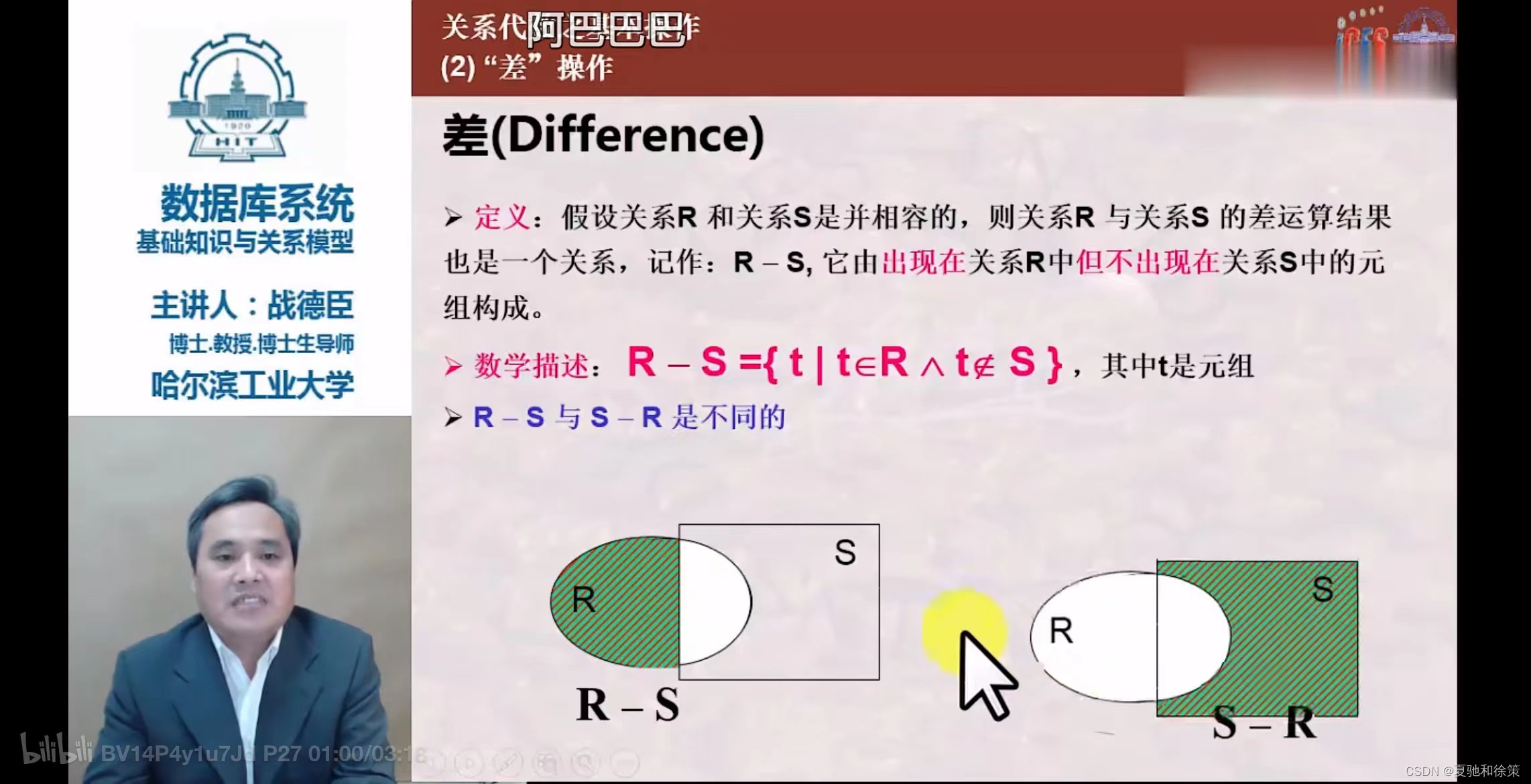
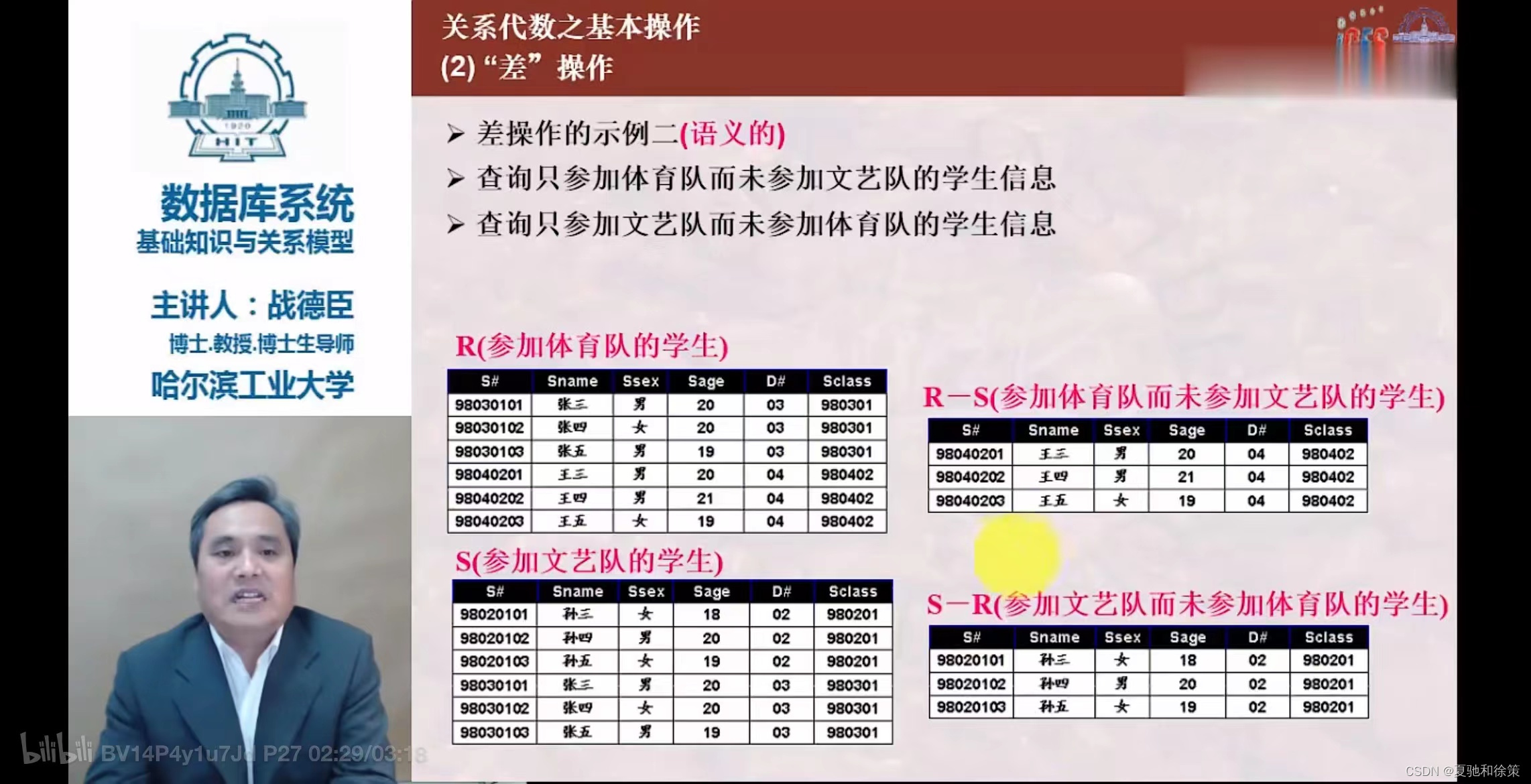
- 符号：R - S
- 条件：同上。
- 结果：包含属于R但不属于S的所有元组的n目关系。

注意:

课后习题2-06第四题就考察了这里主要应用于否定的实现，比如没有使用天津供应商生产的红色零件的工程号JNO.做题的时候我不会我心想哪有这个符号原来是用离散数学集合论里的运算和结论。发现自己思维不灵活的不足，挺好的。这道题目其实就是想告诉我们几点：

第一点：就是在多表连接的时候首先要确定主表，就是和其他表联系最多的表就相当于外键最多，因为只有确定了主表才能相应的运用我下面总结的结论，即连接最小空间理论，才能确定哪些是外表哪些是主表那些是外键。

第二点：差运算可以用来表示没有

第三点：找主表的结论

结论：

找主表法：

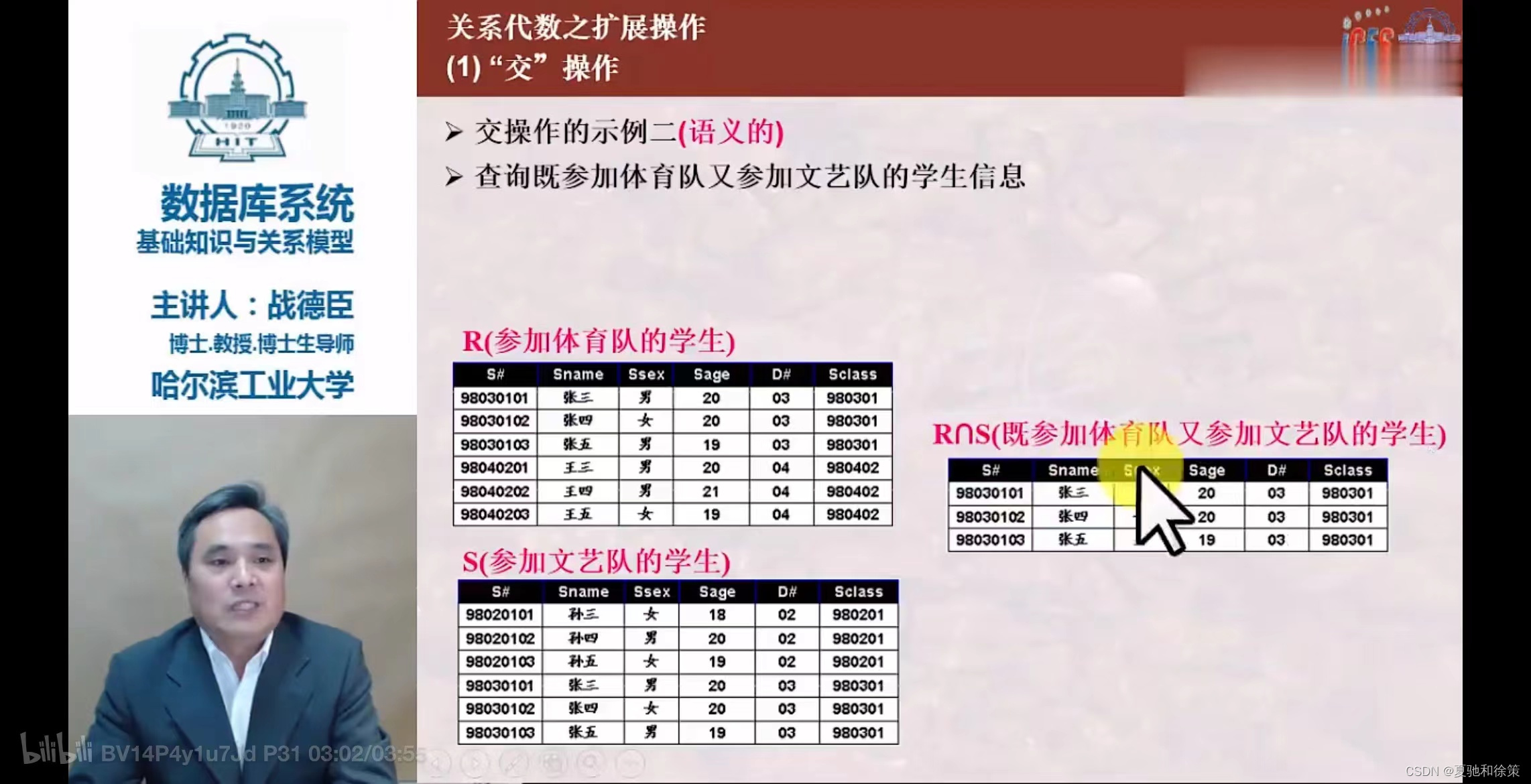
交 (Intersection)
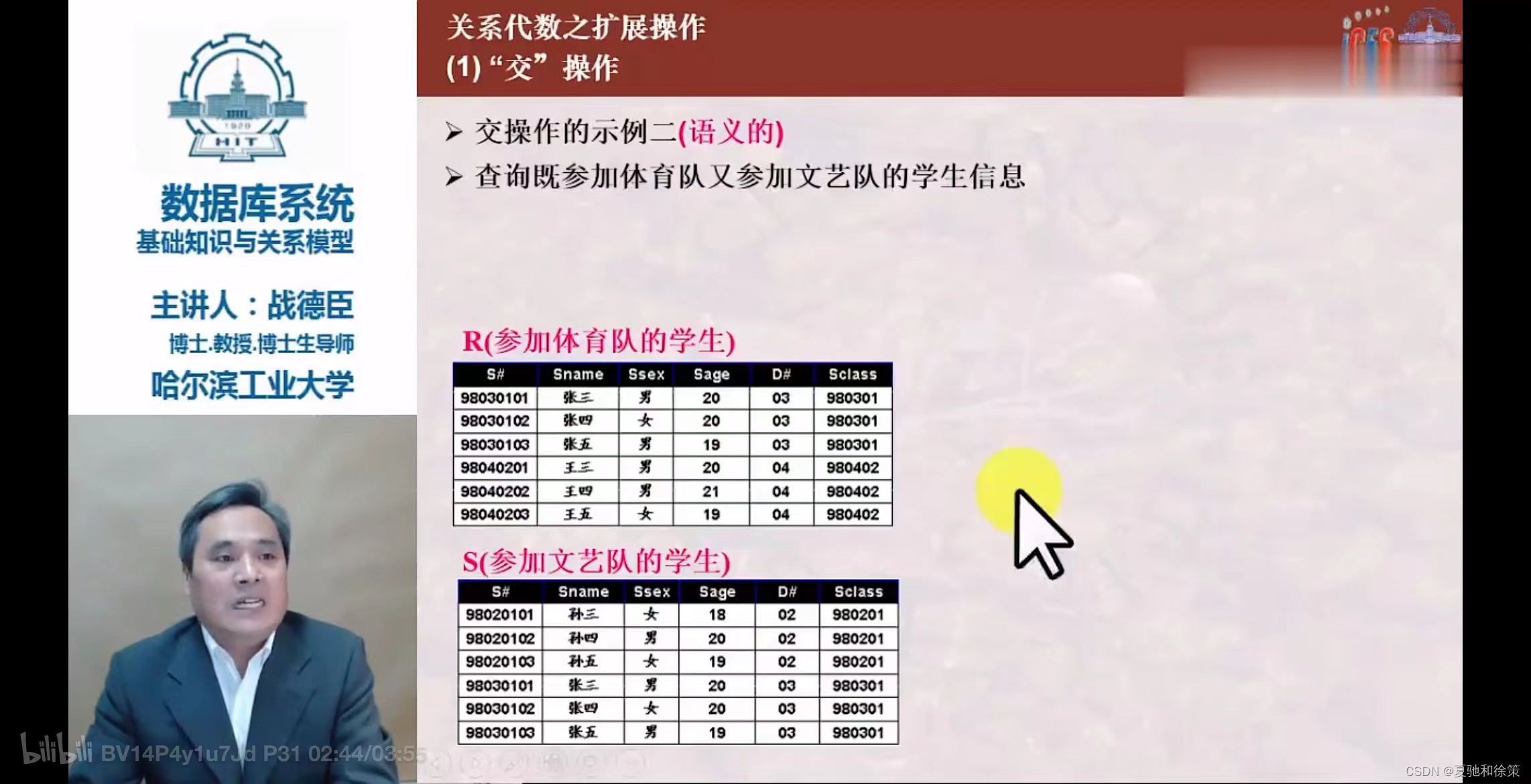
- 符号：R ∩ S
- 条件：同上。
- 结果：包含既属于R又属于S的所有元组的n目关系。
- 注：交运算可以通过差运算来实现，即R ∩ S = R - (R - S)。
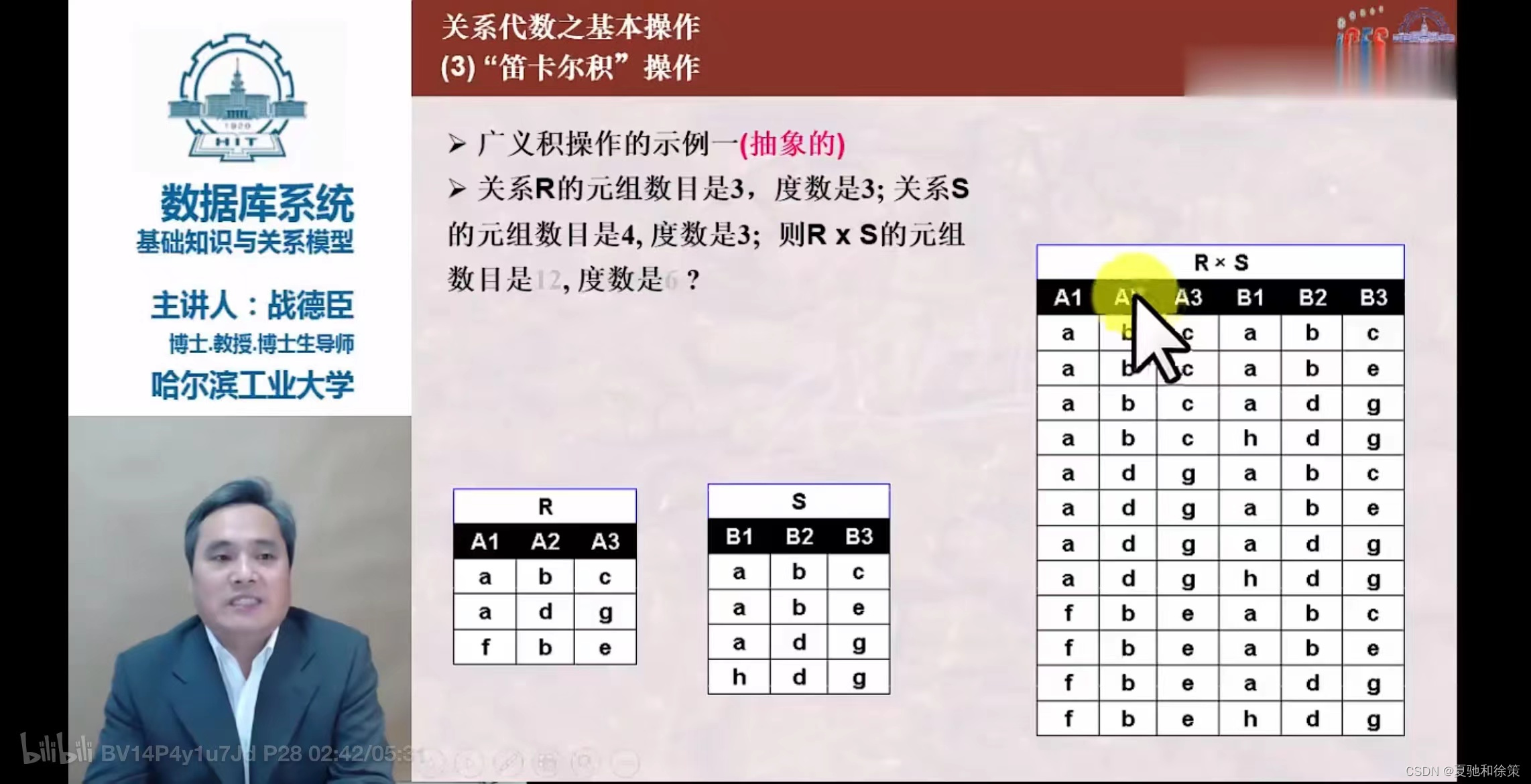
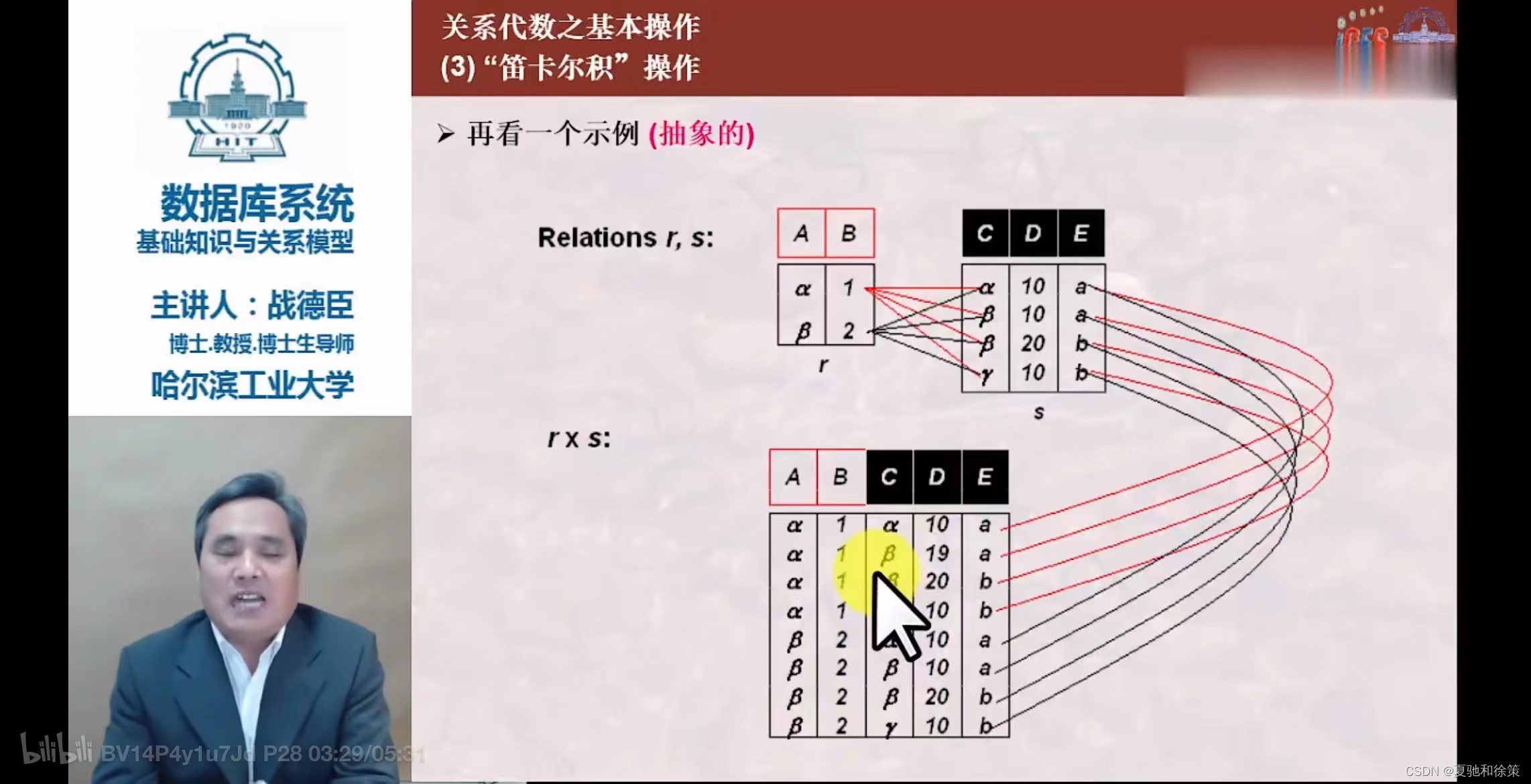
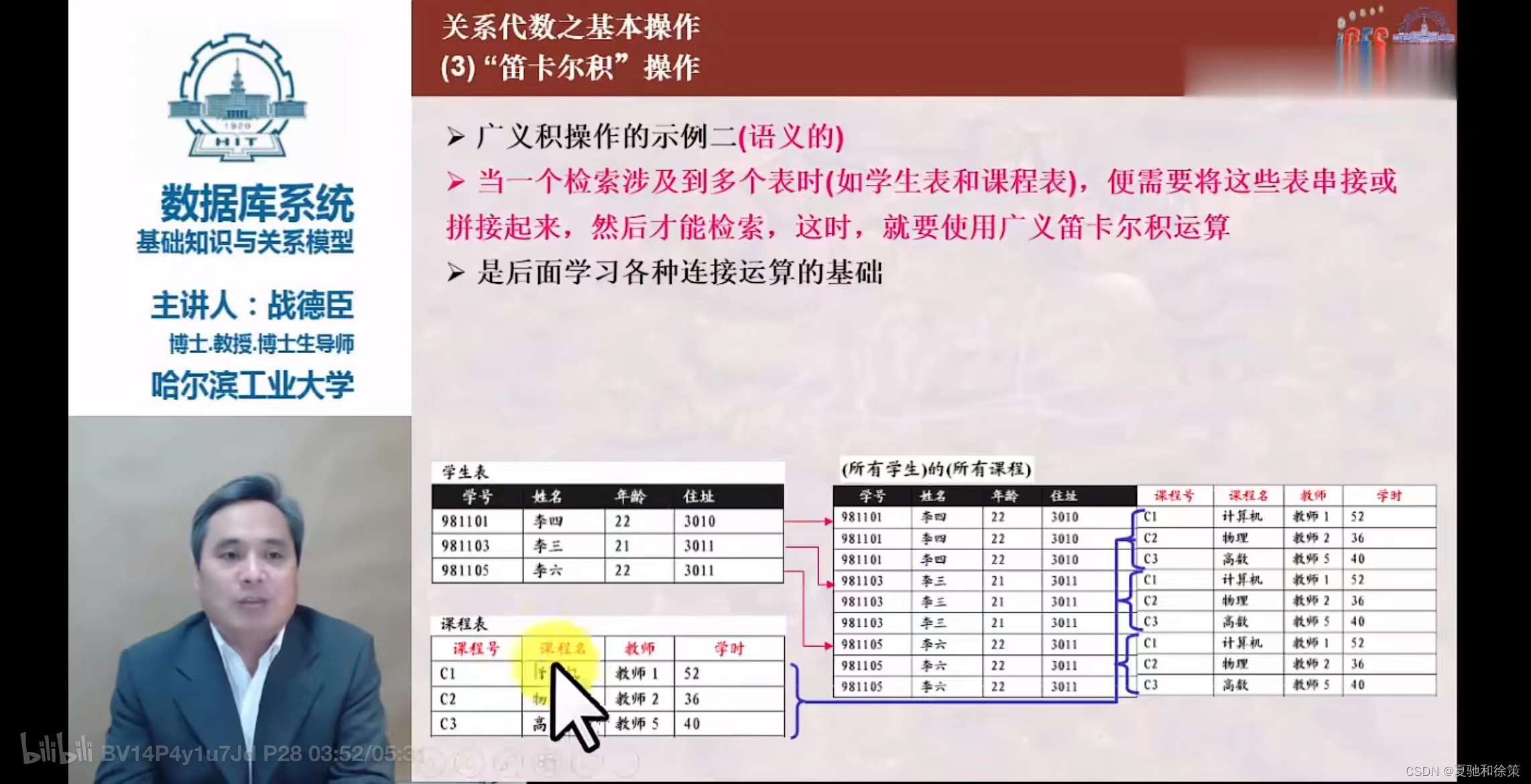
笛卡尔积 (Cartesian Product)
- 符号：R × S
- 条件：R为n目关系，S为m目关系。
- 结果：一个(n+m)列的元组的集合，其中元组的前n列来自R，后m列来自S。
- 特点：若R有k₁个元组，S有k₂个元组，则结果有k₁×k₂个元组。

图解示例

图2.2(a) & (b) 展示了具有三个属性的关系R和S。
图2.2(c) 为R和S的并。
图2.2(d) 为R和S的交。
图2.2(e) 为R和S的差。
图2.2(f) 为R和S的笛卡尔积。

2.4.2 专门的关系运算

概述

专门的关系运算 包括选择（Selection）、投影（Projection）、连接（Join）、除（Division）等。
为方便叙述，先引入一些基本记号。

基本记号

关系模式与元组：设关系模式为 R(A₁, A₂, ..., An)，其中 t ∈ R 表示 t 是 R 的一个元组。t[Ai] 表示元组 t 中对应于属性 Ai 的分量。
属性列或属性组：如果 A = {An, Az, ..., Au} 是 Aj, A₂, ..., An 中的一部分，则 A 称为属性列或属性组。t[A] = (t[An], t[Az], ..., t[Au]) 表示元组 t 在属性列 A 上的分量集合。

专门关系运算

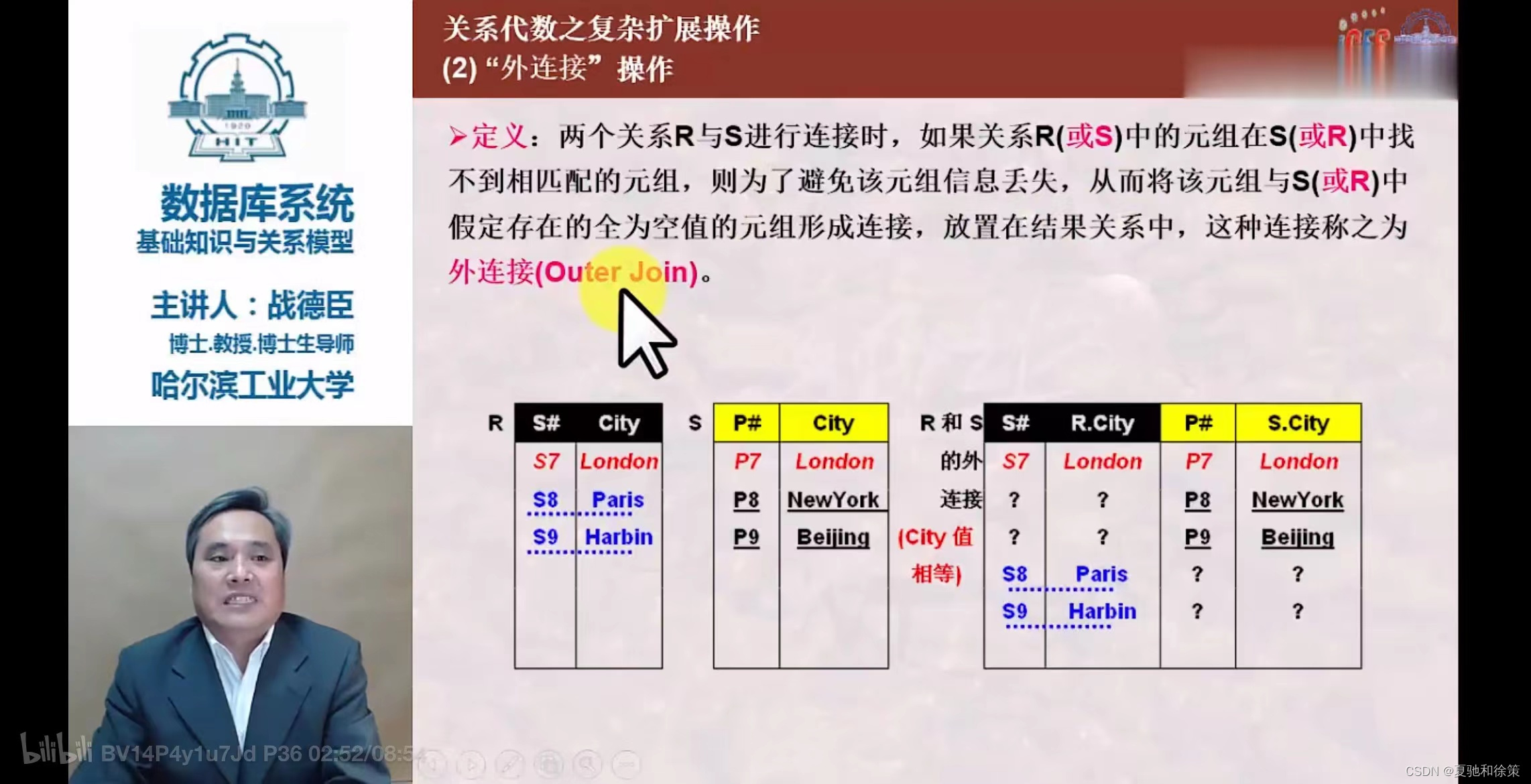
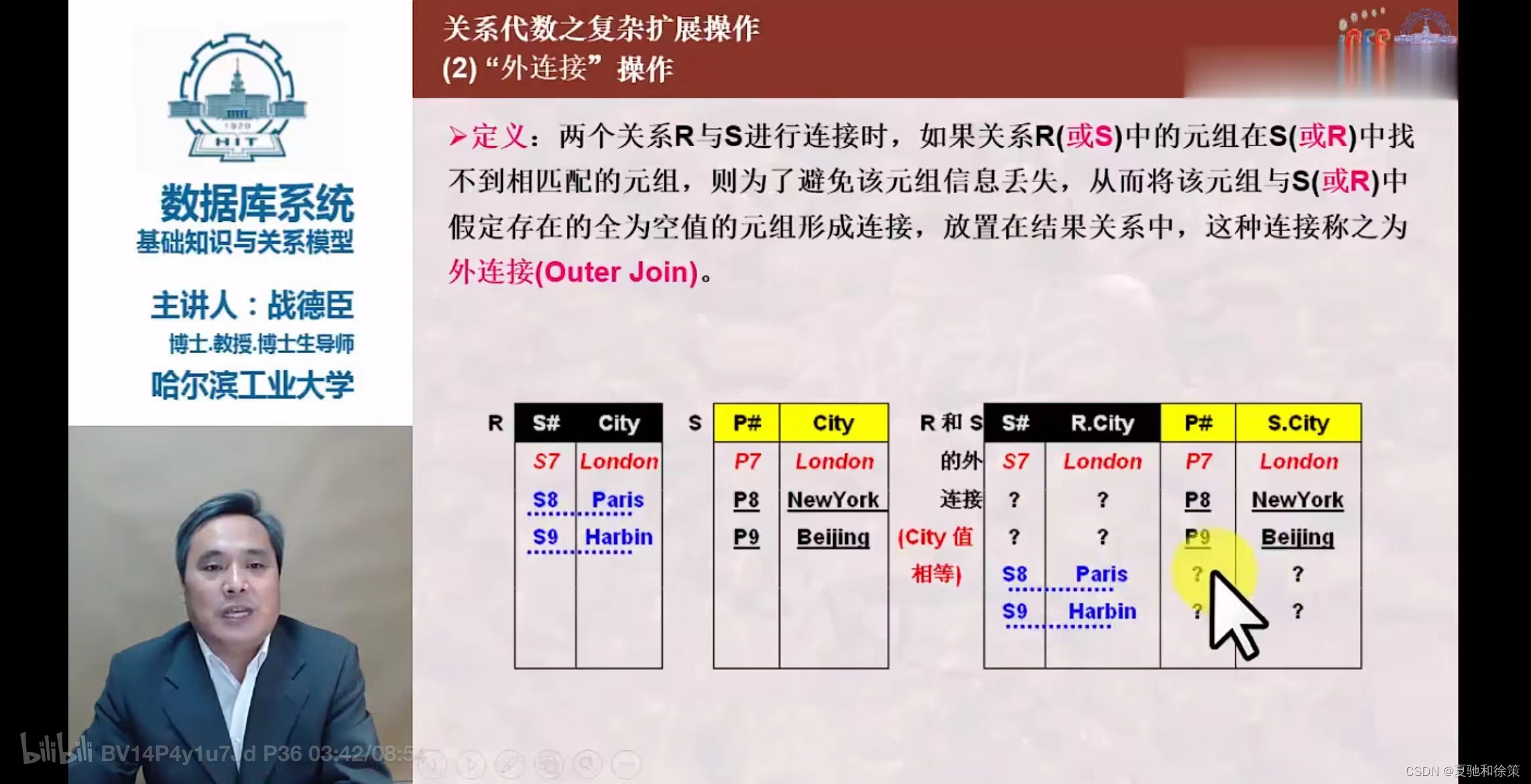
外连接常用于查询那些在一个表中但不在另一个表中的记录，或者在两个表中都有但是需要合并结果的情况。它是数据库查询中非常重要的一部分，能够提供比内连接（Inner Join，只返回两个表中匹配的记录）更全面的数据视图。

1.选择(SELECT)

注意：

课后习题2-06第二题考察了and逻辑与在关系代数中选择的时候如果想表示都成立那么我们可以用^这个符号，在我的记忆库中很容易出错，原因就是我把第三章的SQL语句SELECT的AND和它混淆了，又发现了自己的不足还是很有收获的。

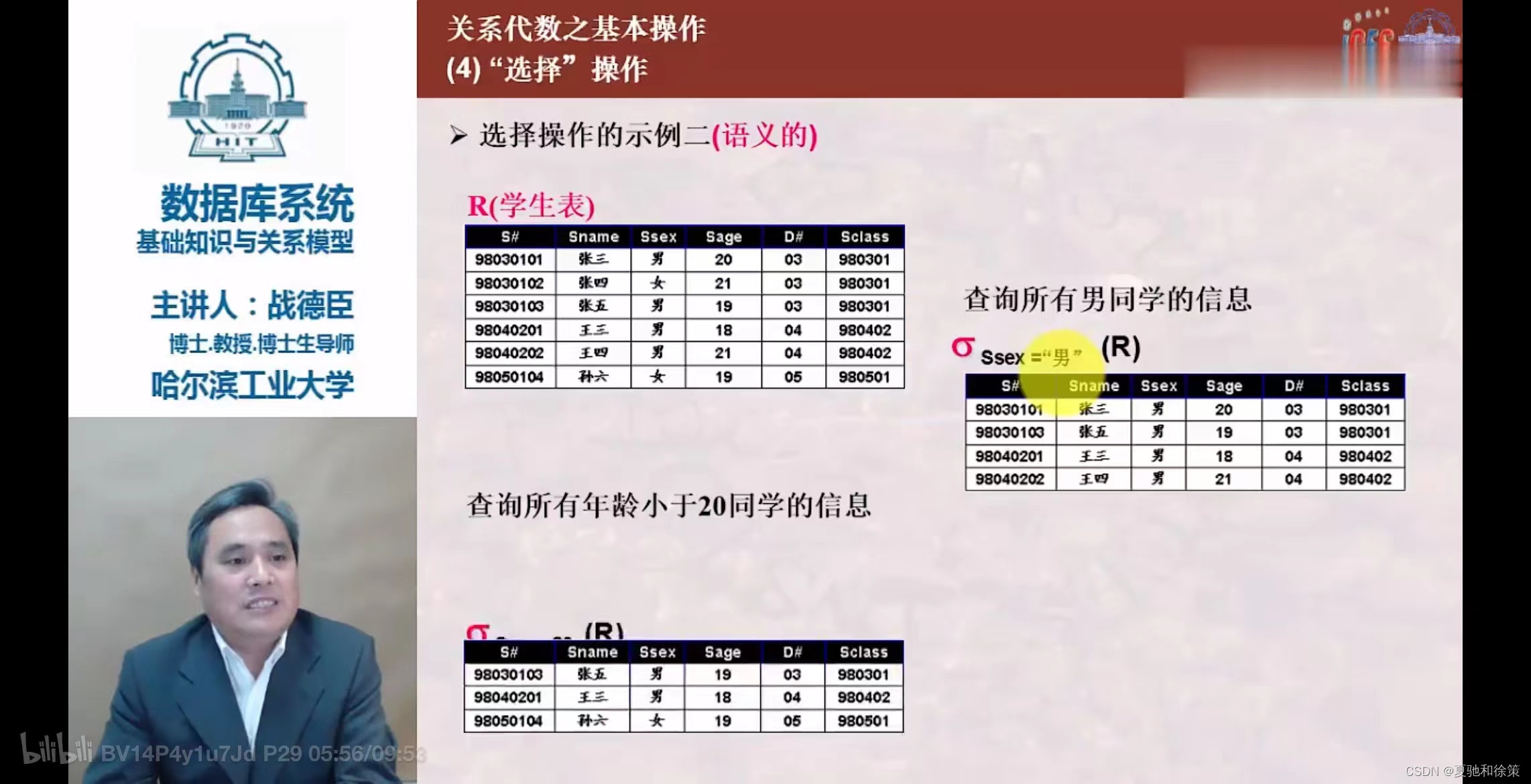
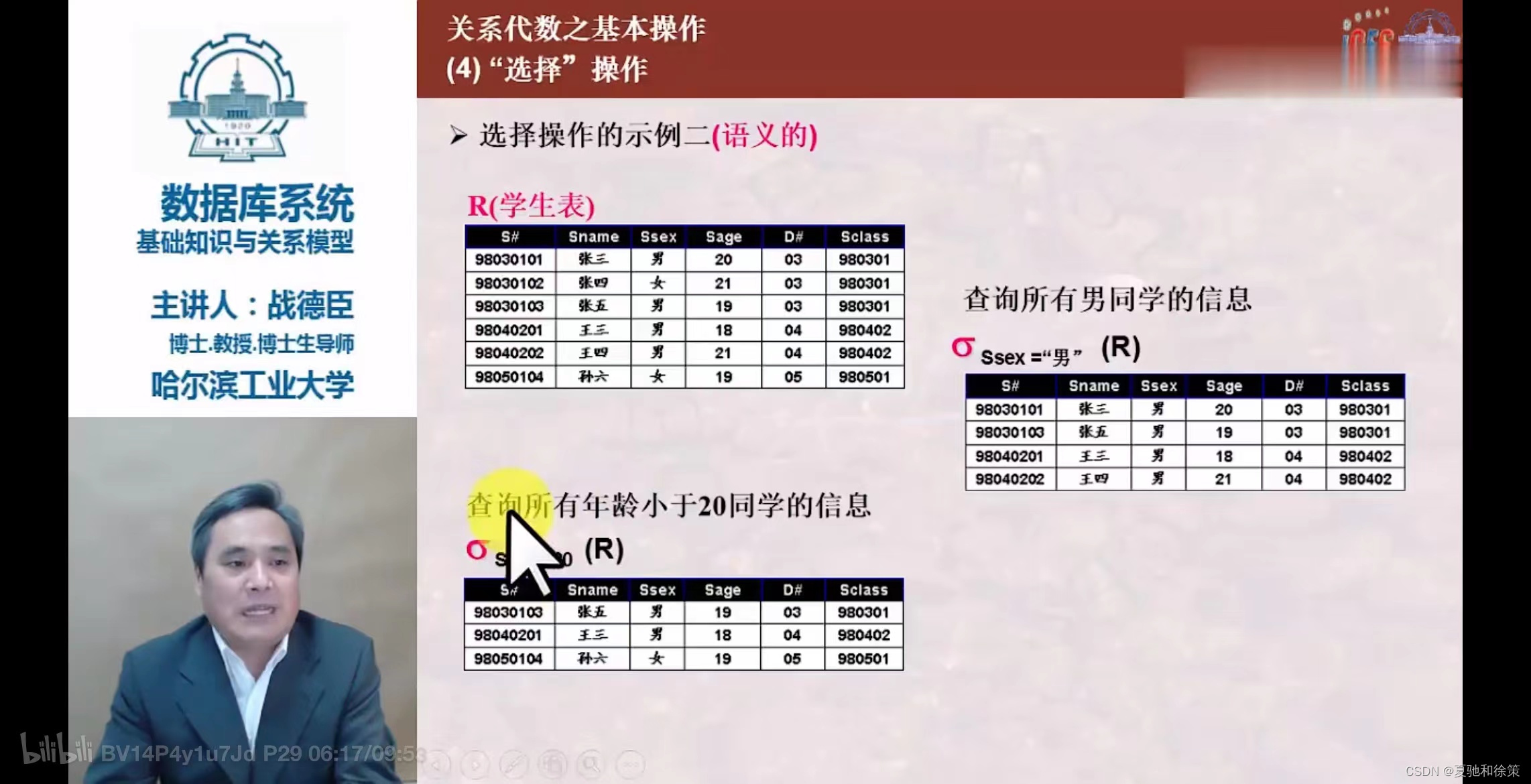
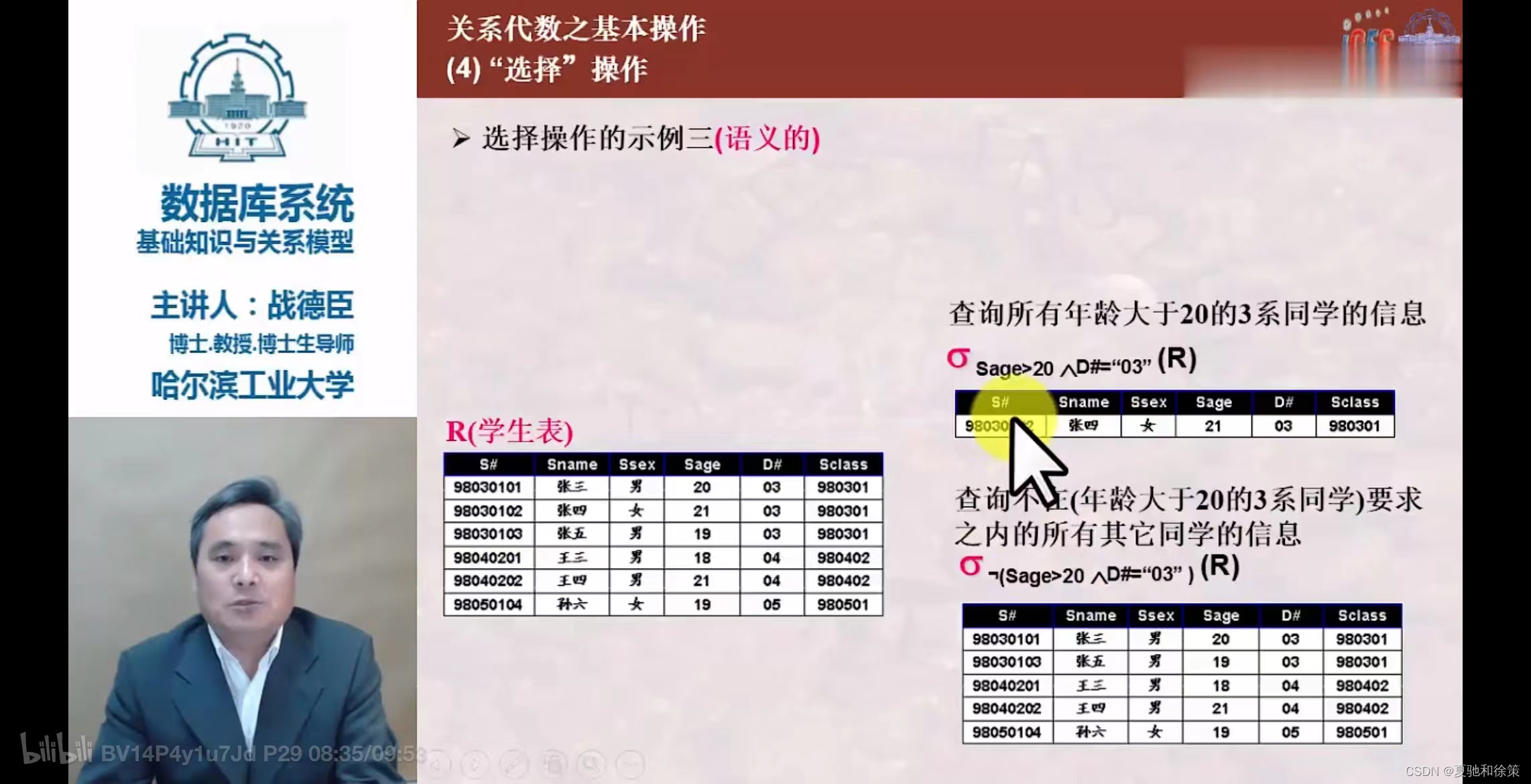
- 用于在关系 R 中选择满足给定条件的元组。
- 条件是逻辑表达式，取值为“真”或“假”。

2.投影（Projection）

注意：课后习题2-06第三题我错了，这道题目告诉我们几件事，第一件选择运算后会得到一个一个元组，而元组有很多不必要的属性，而我错就错在应该在选择出这些元组后通过投影把这些多余的属性给筛除掉，这样减少负担。下图是我的答案和结论：

连接最小空集结论：

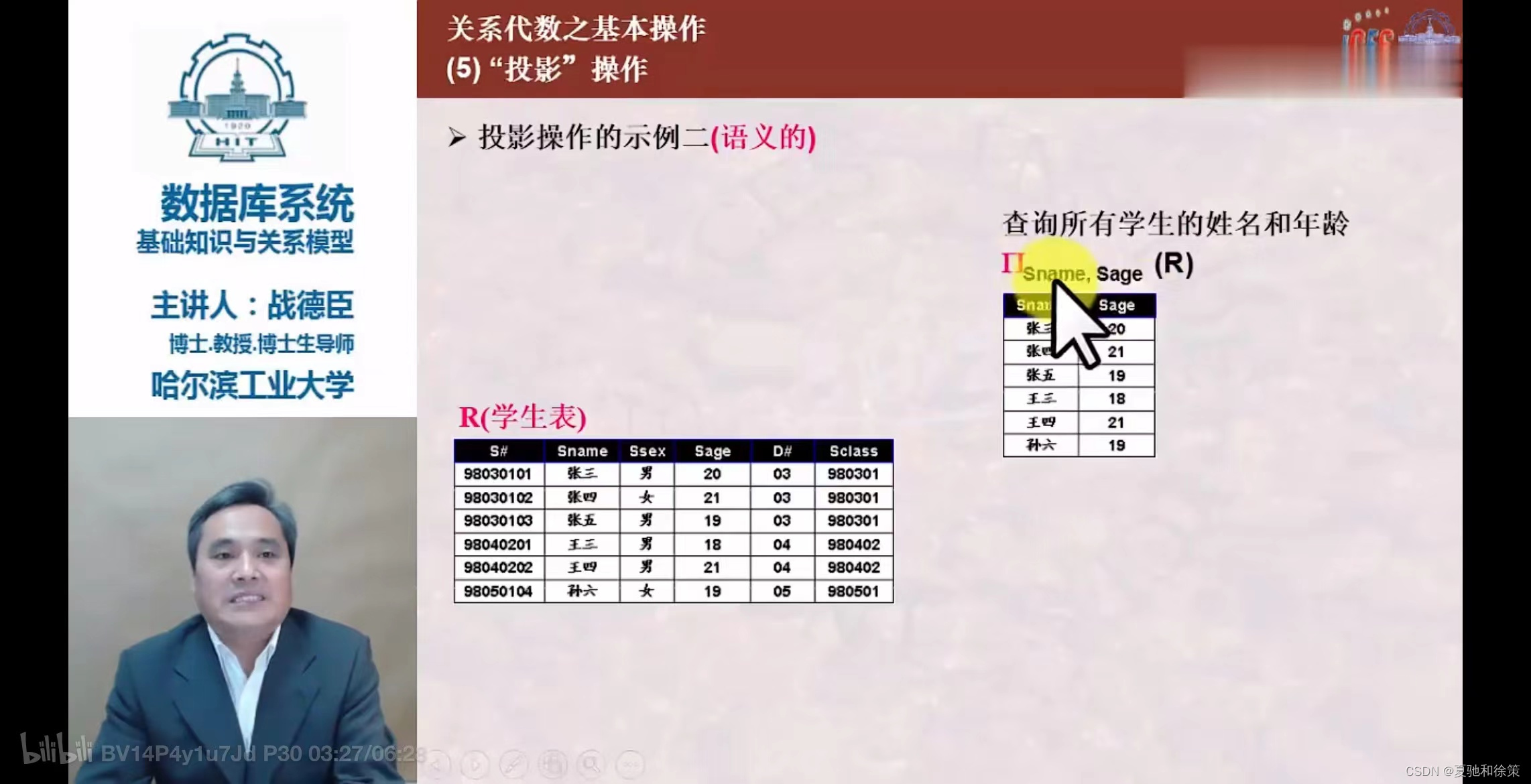
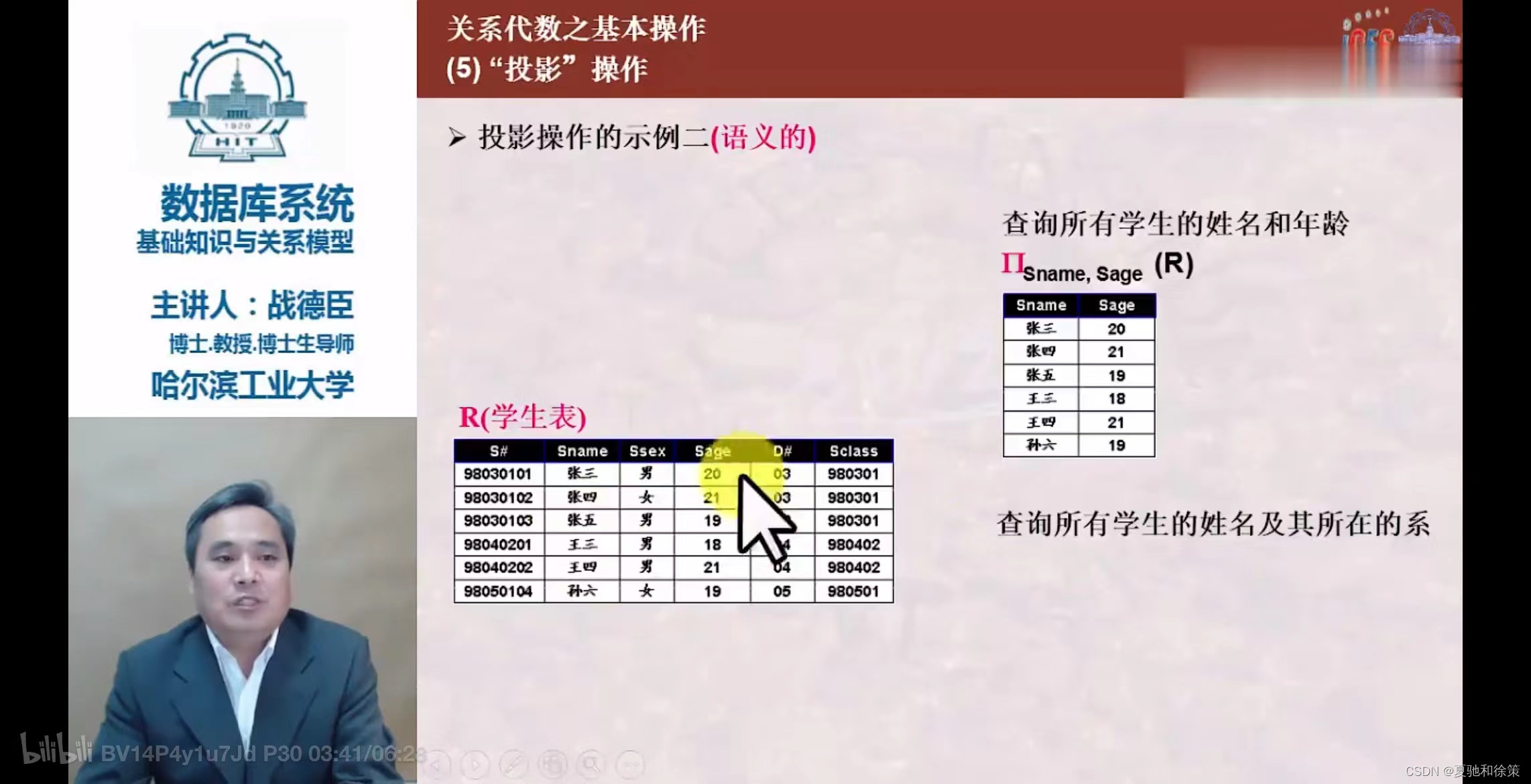
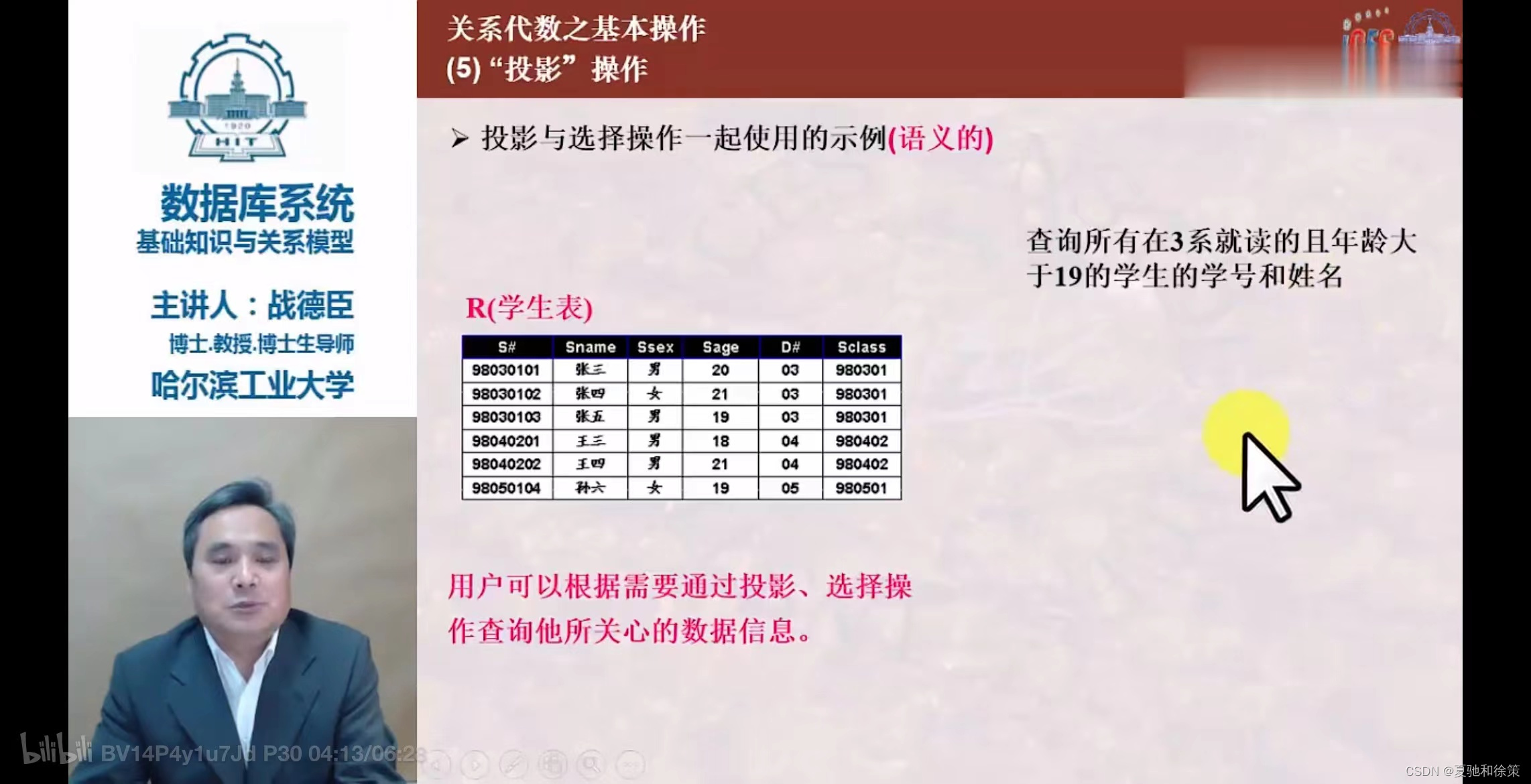
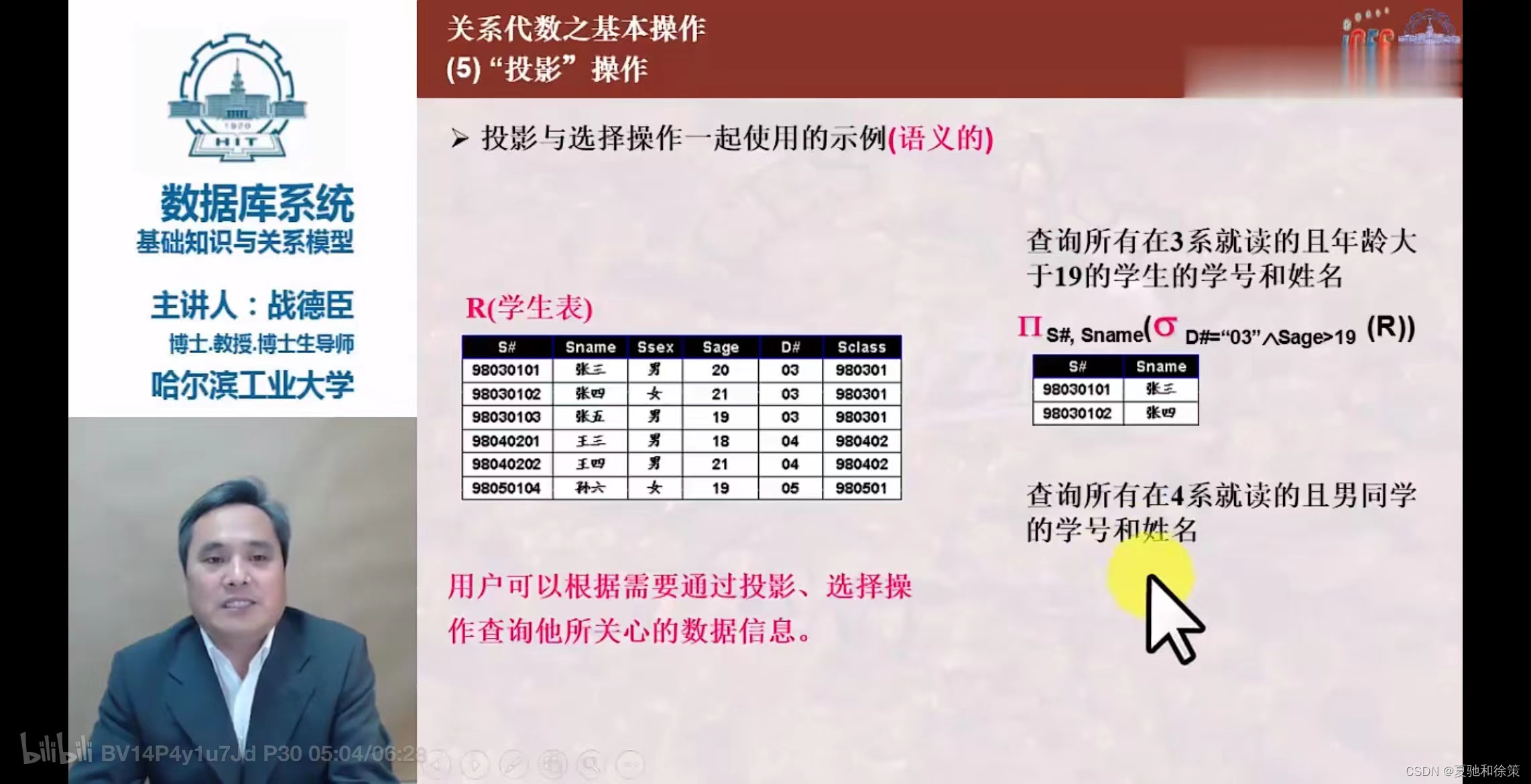
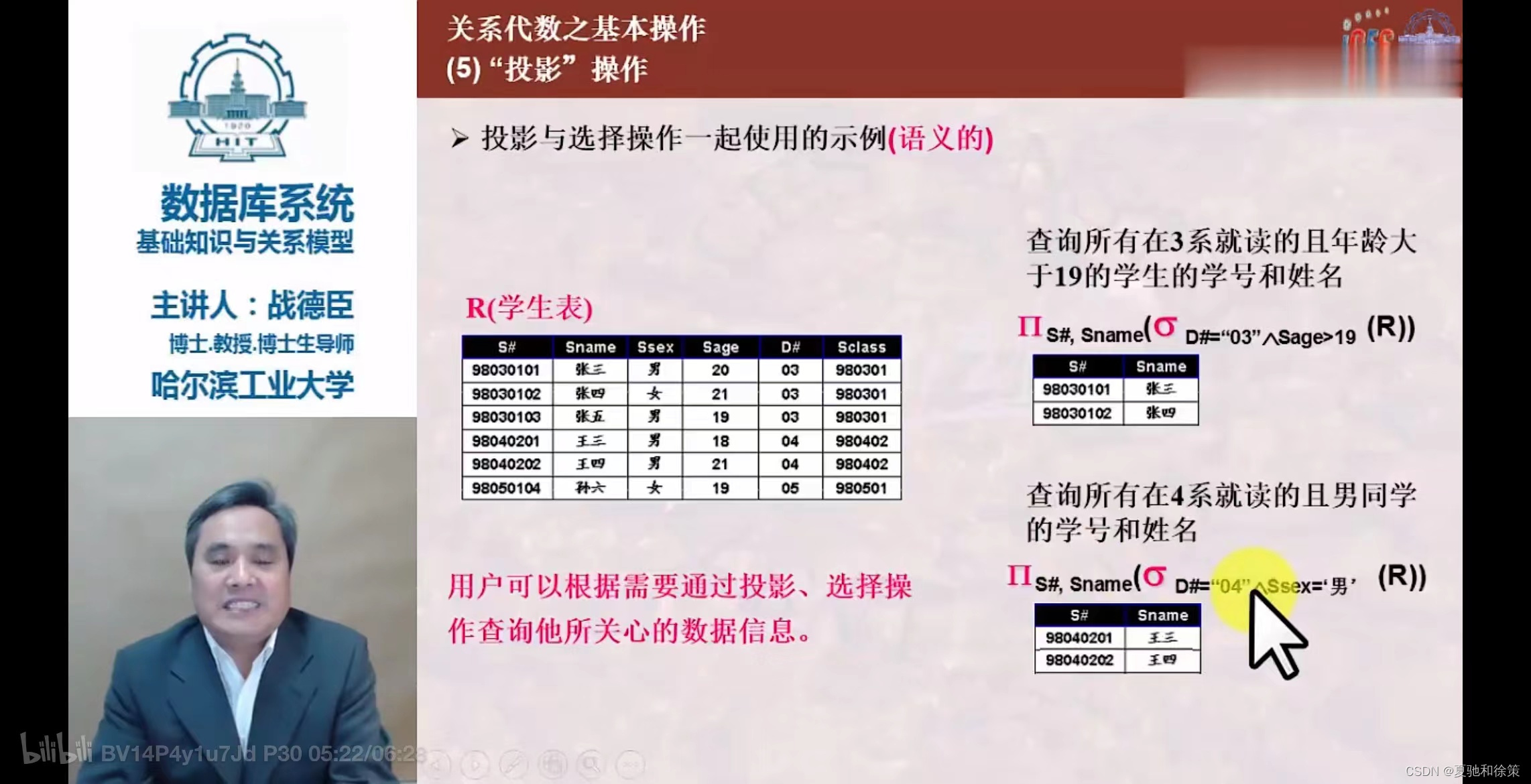
- 从关系 R 中选择出若干属性列组成新关系。
- 投影操作从列的角度进行运算。

3.连接（Join）

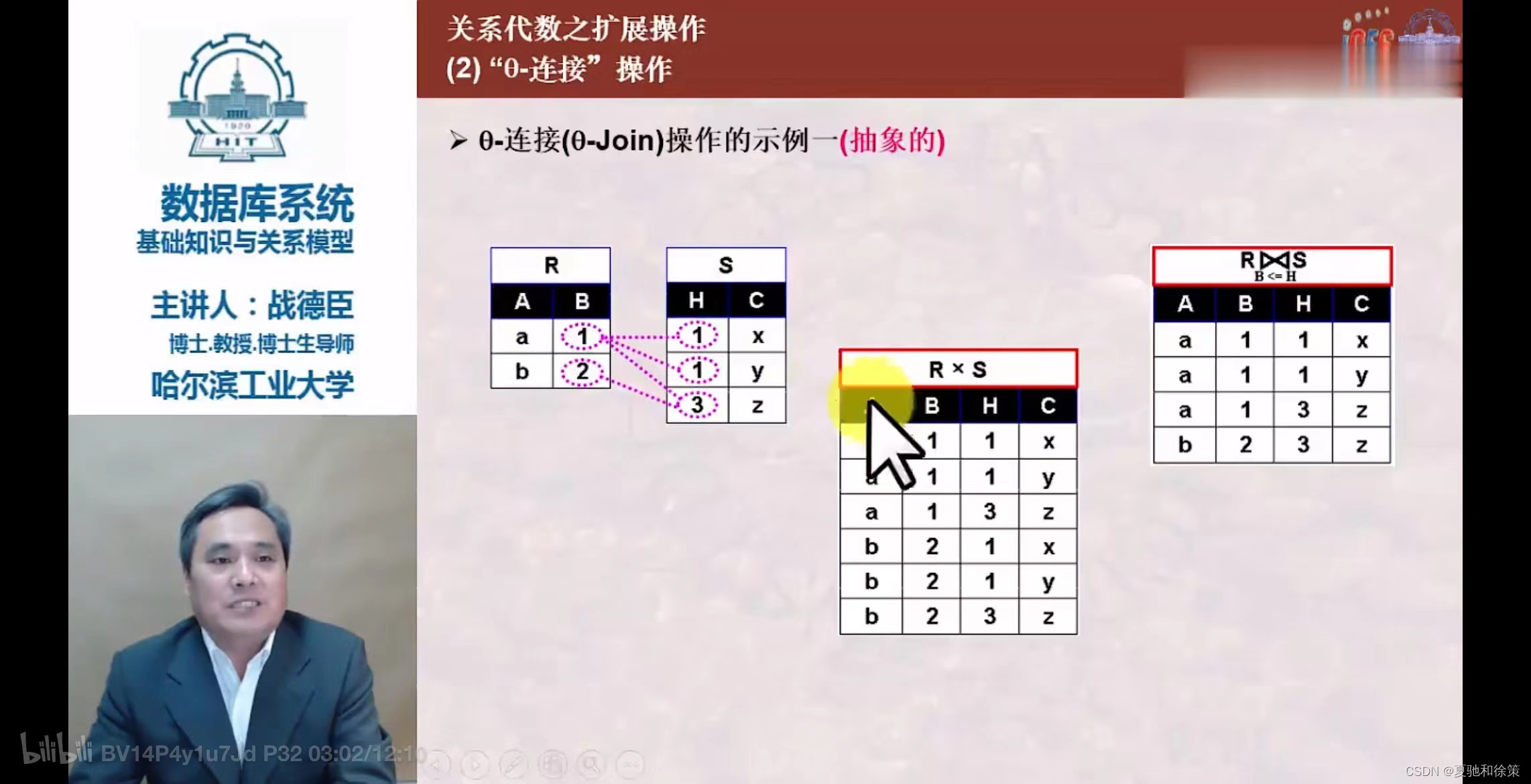
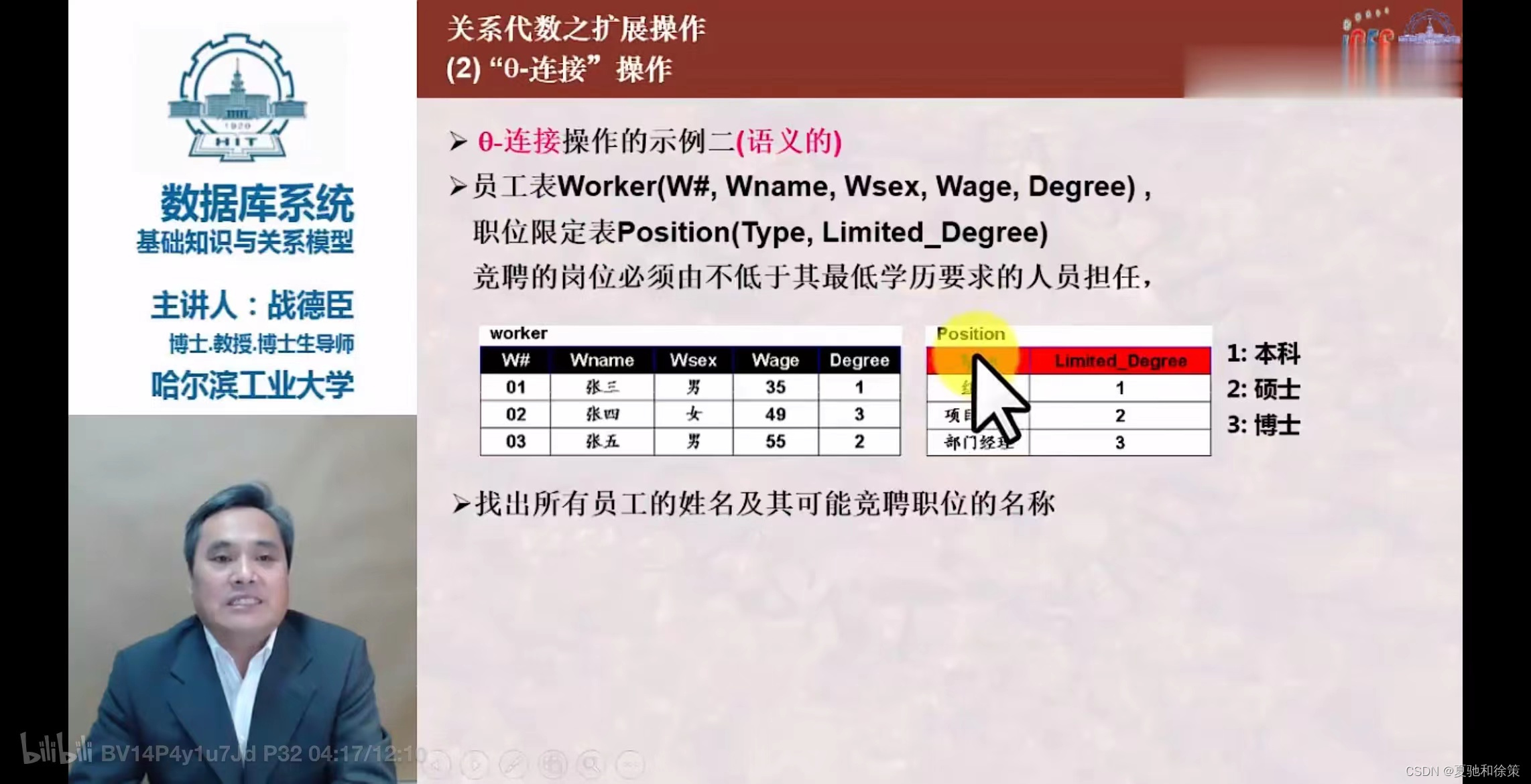
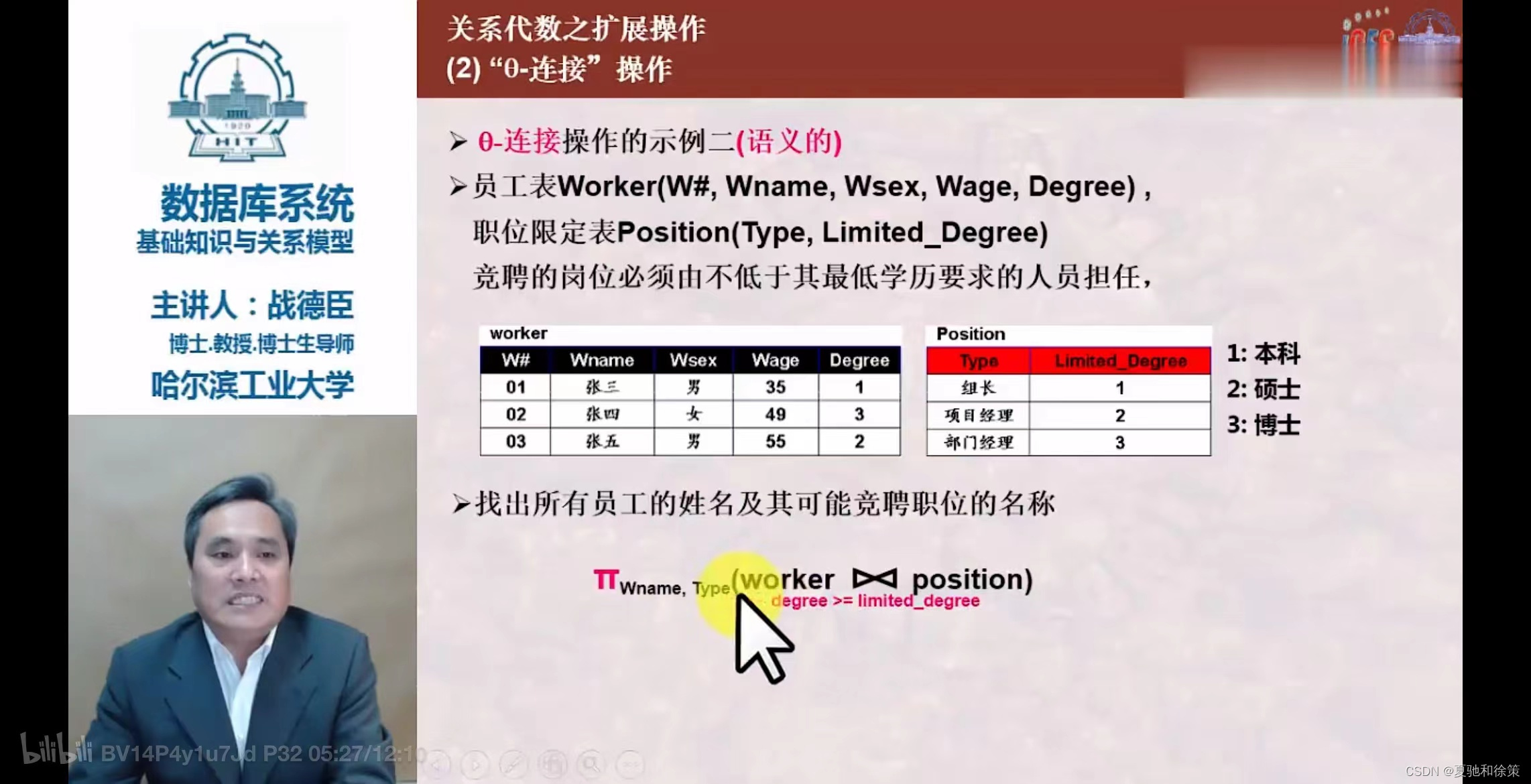
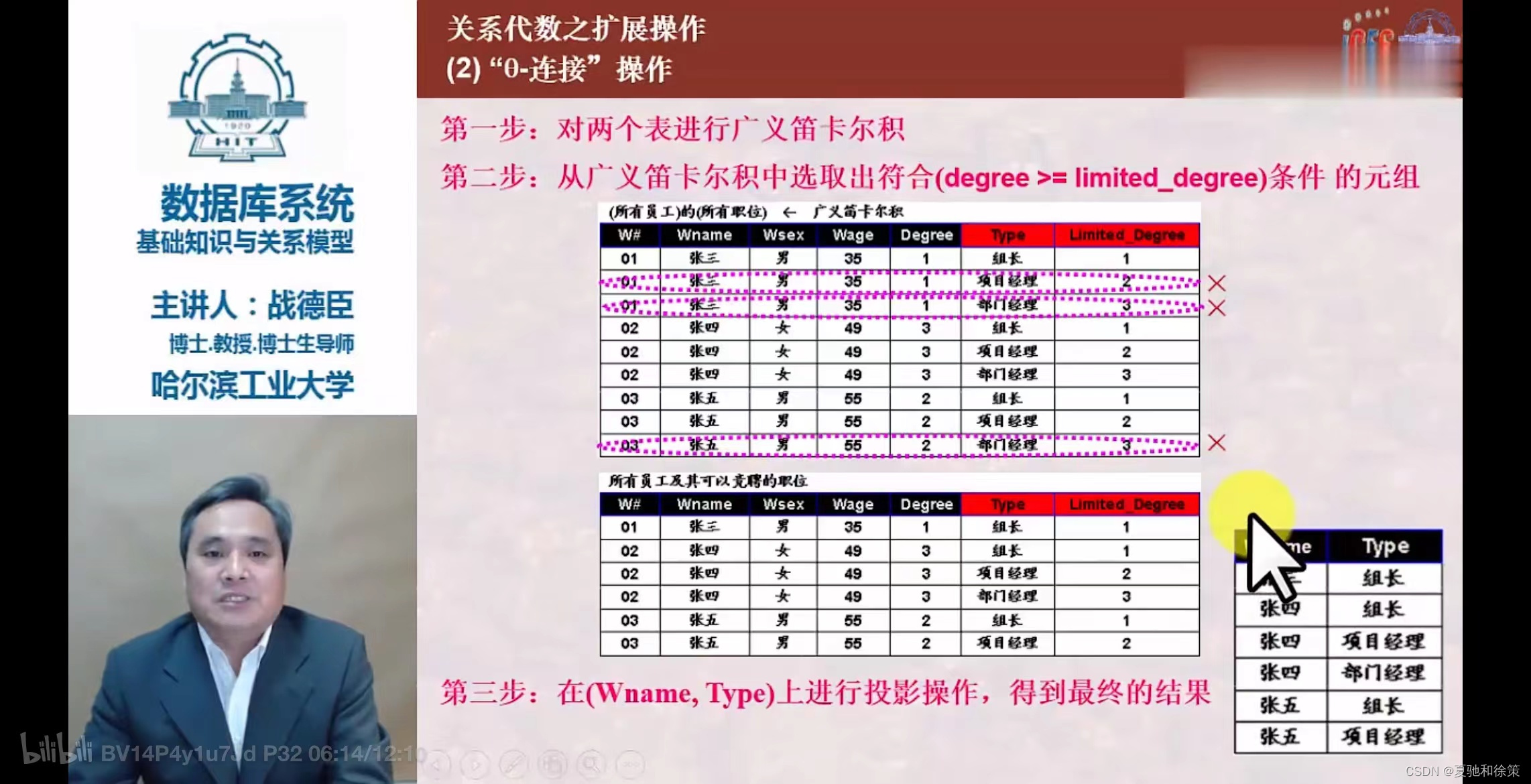
- 从两个关系的笛卡尔积中选取属性间满足特定条件的元组。
- 包括等值连接和自然连接。
- 等值连接：
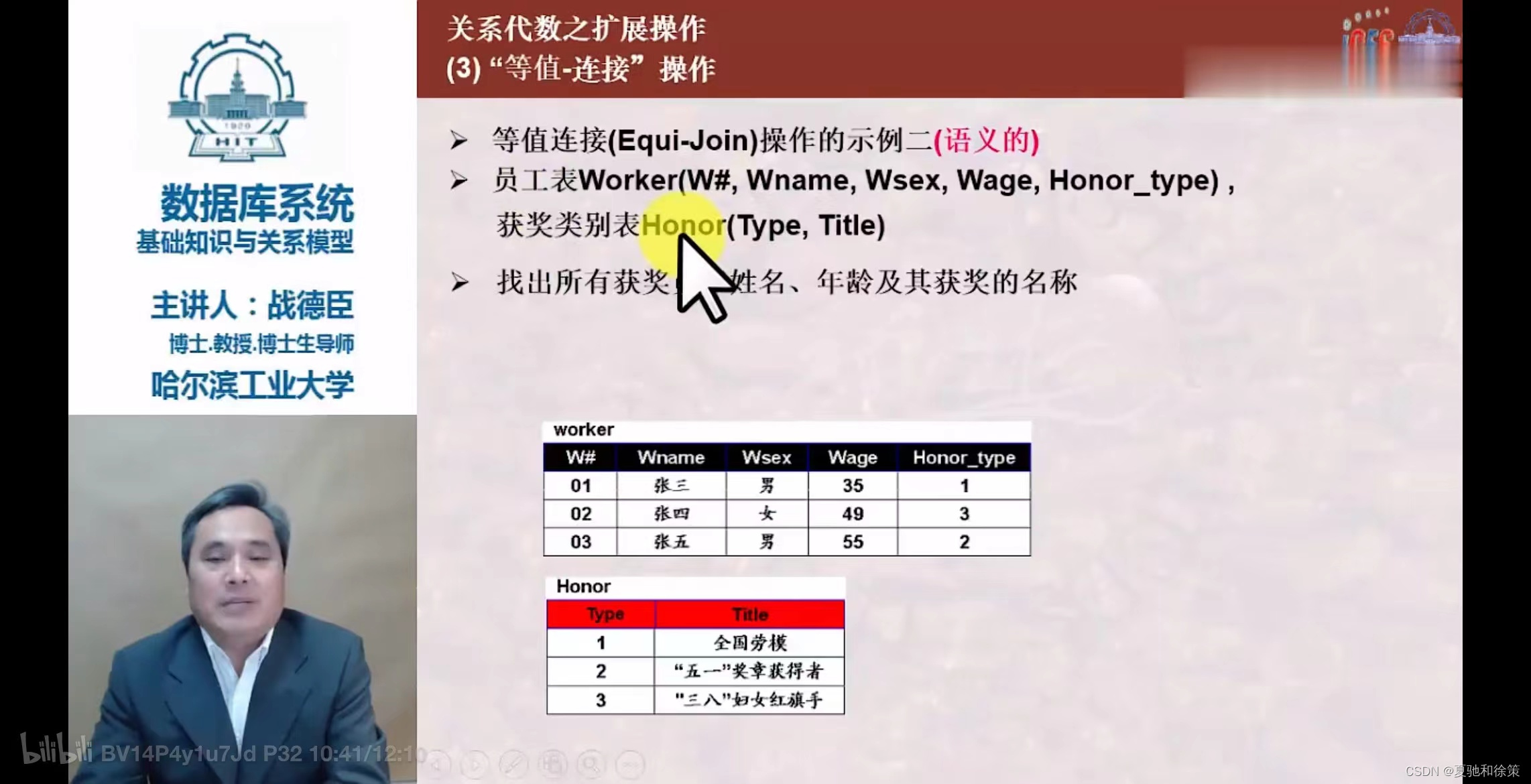
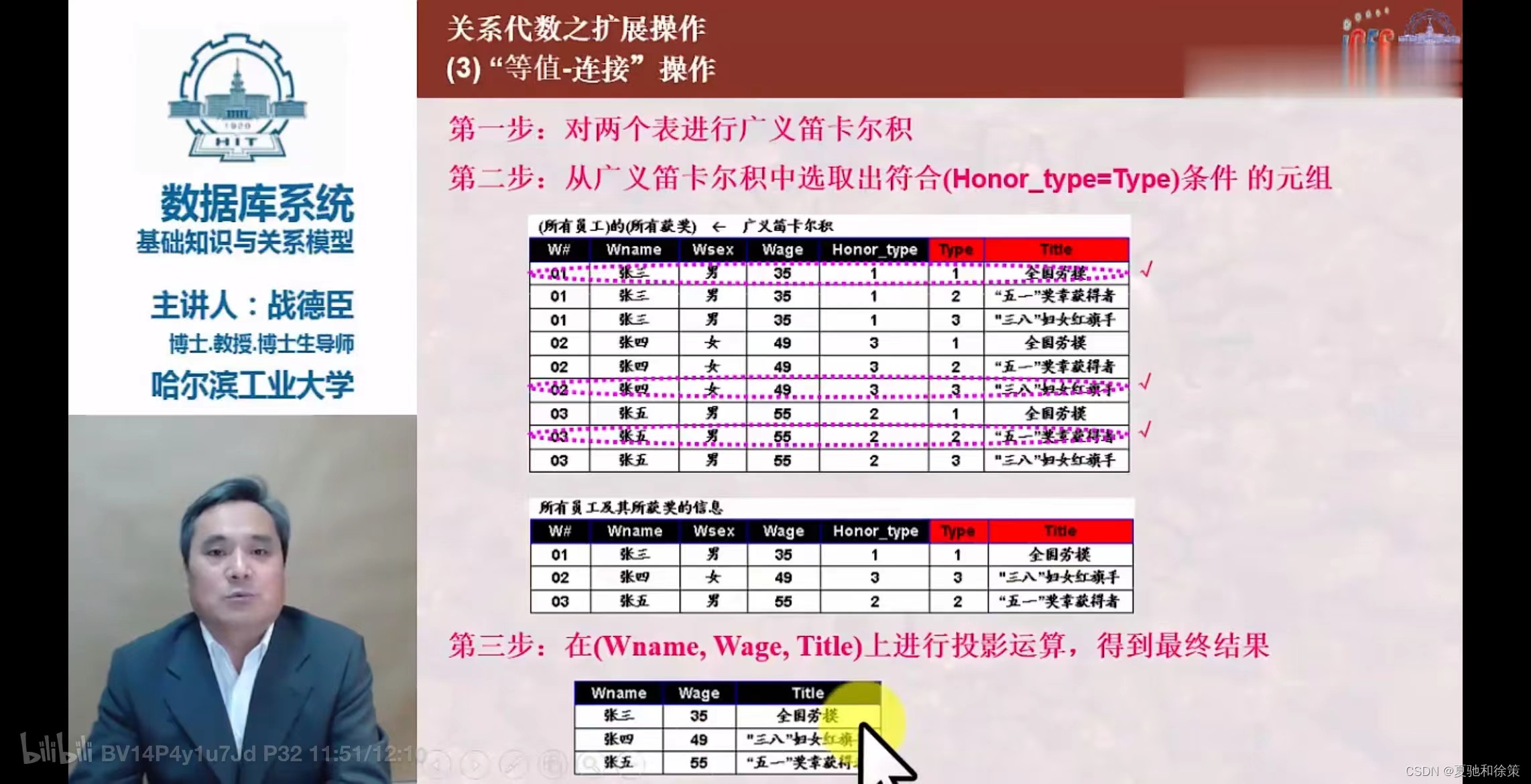
- 自然连接：
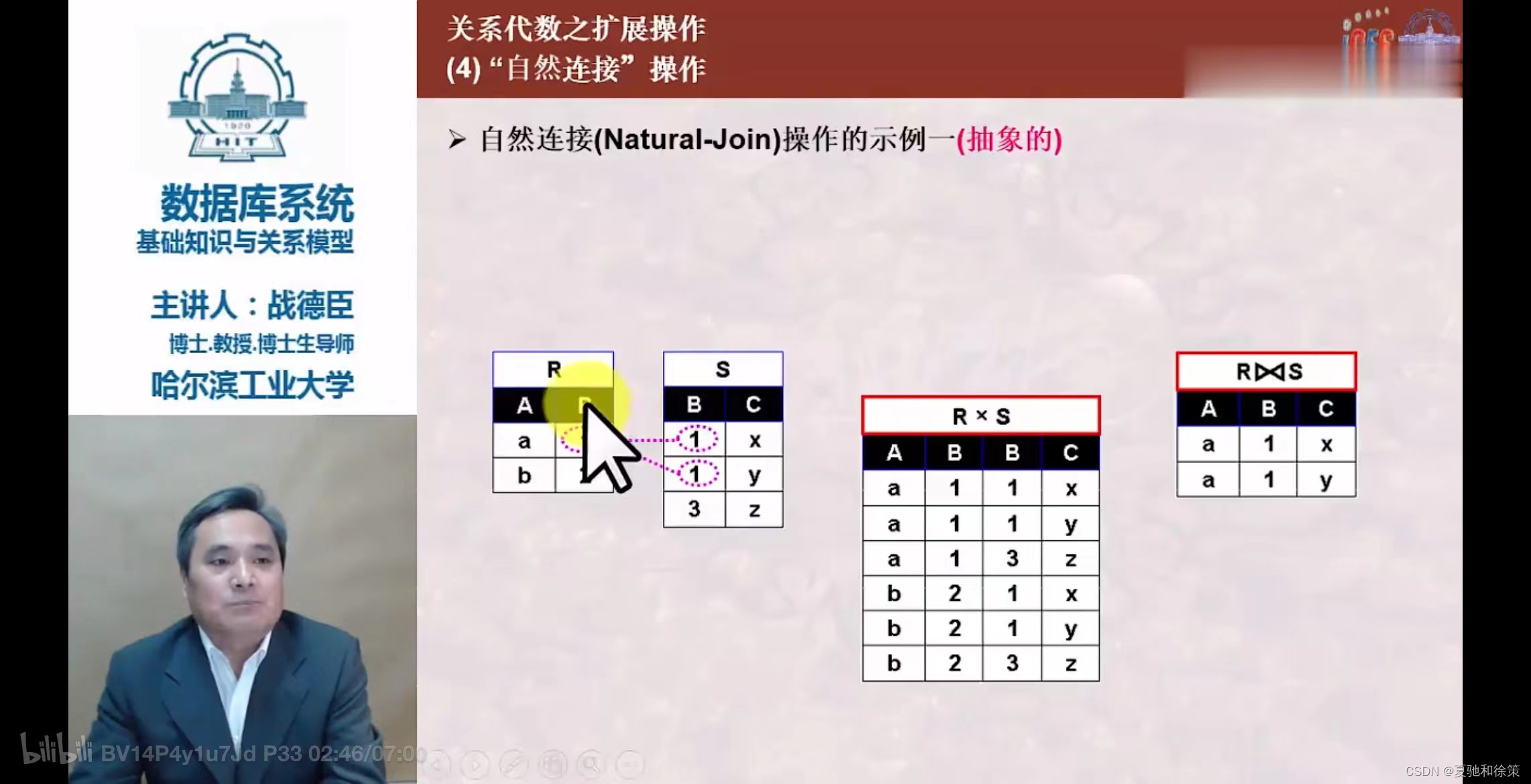
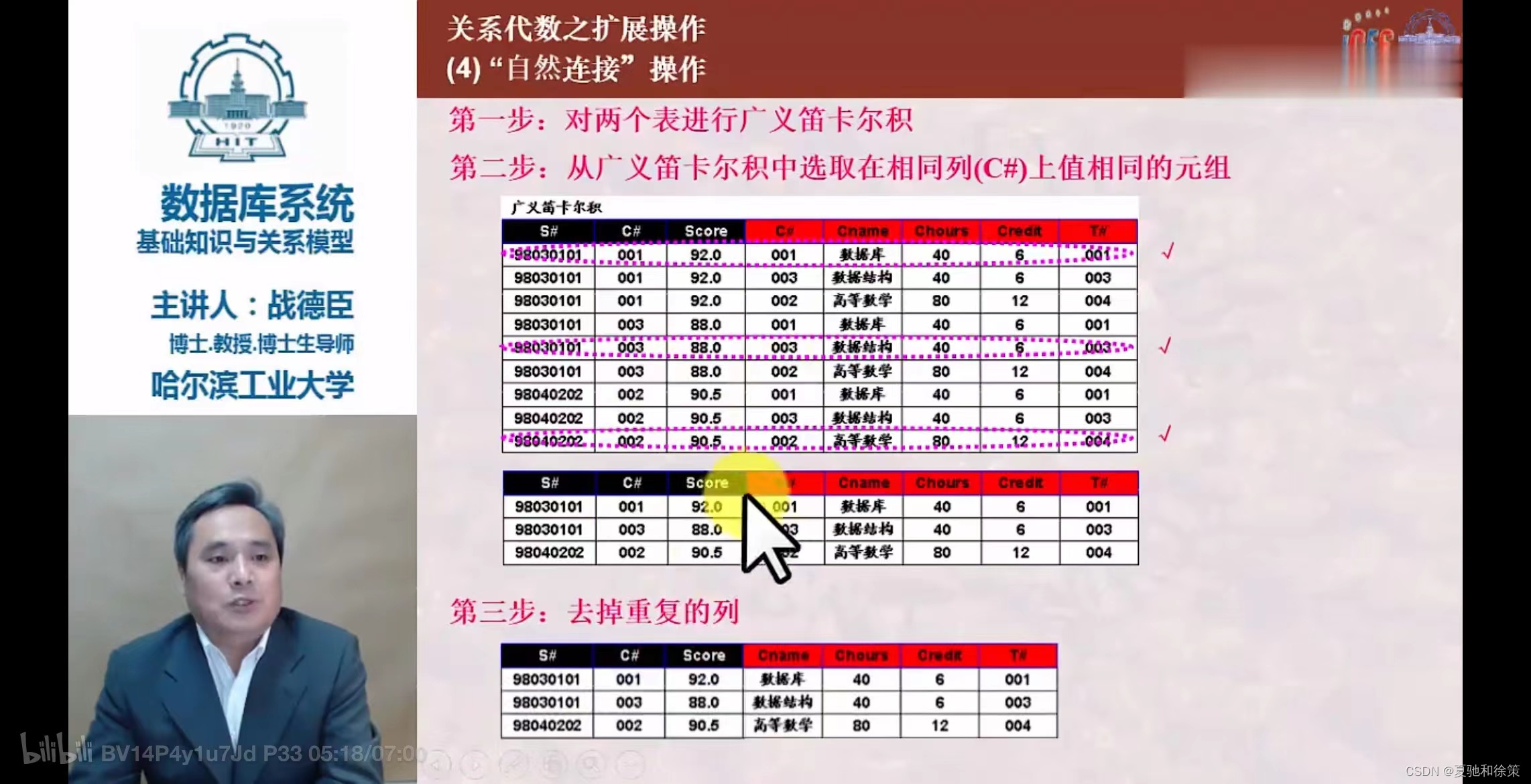
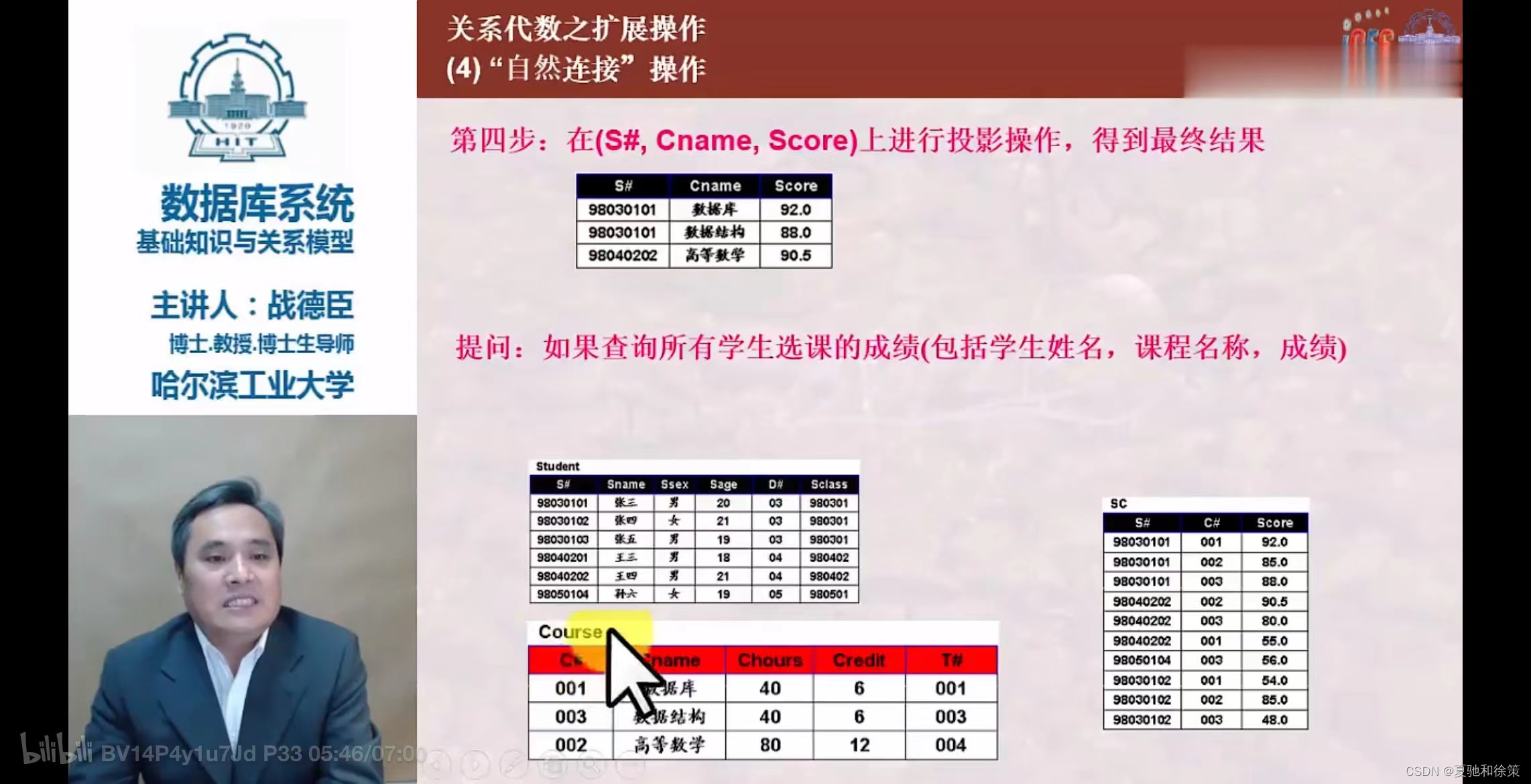
除（Division）
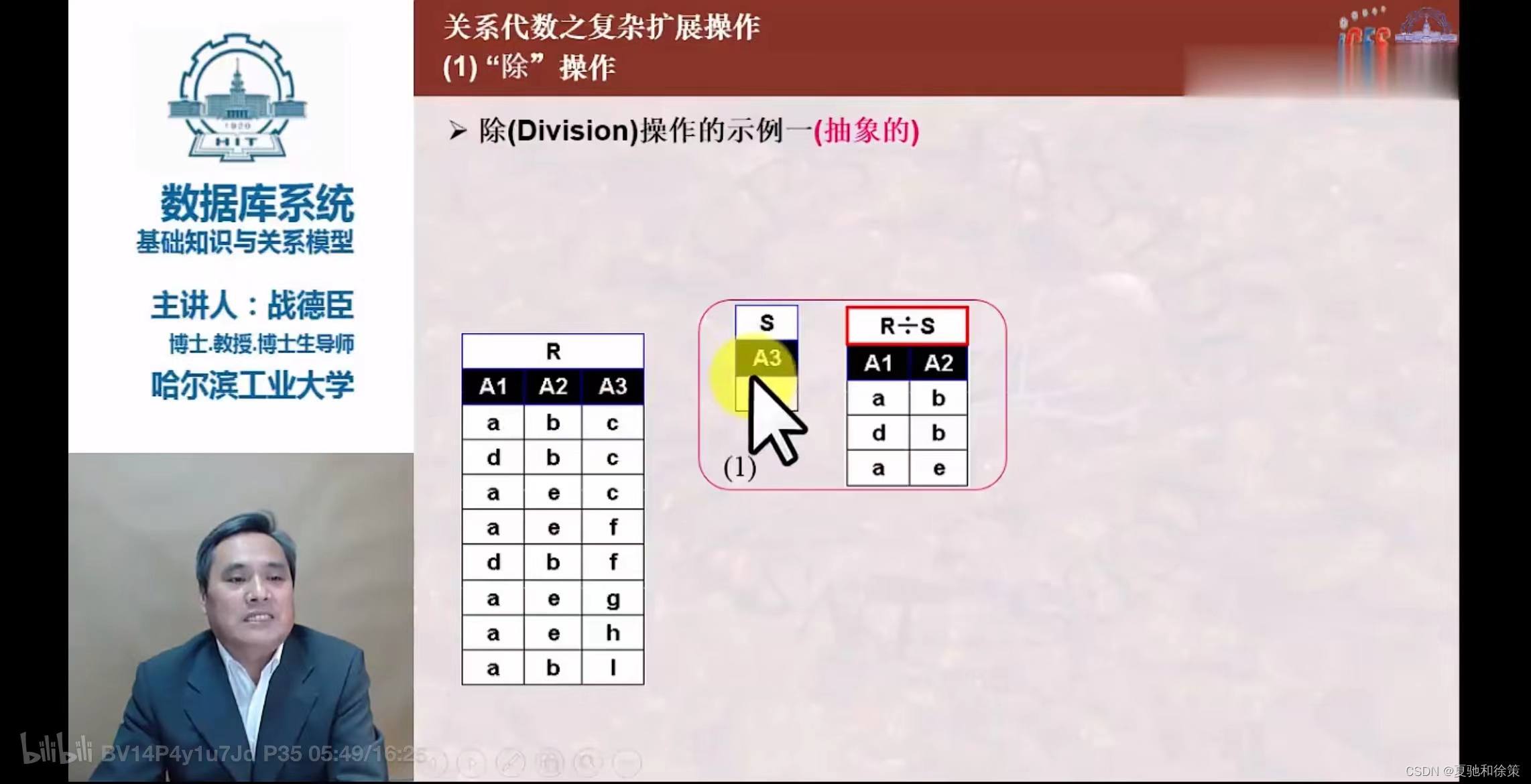
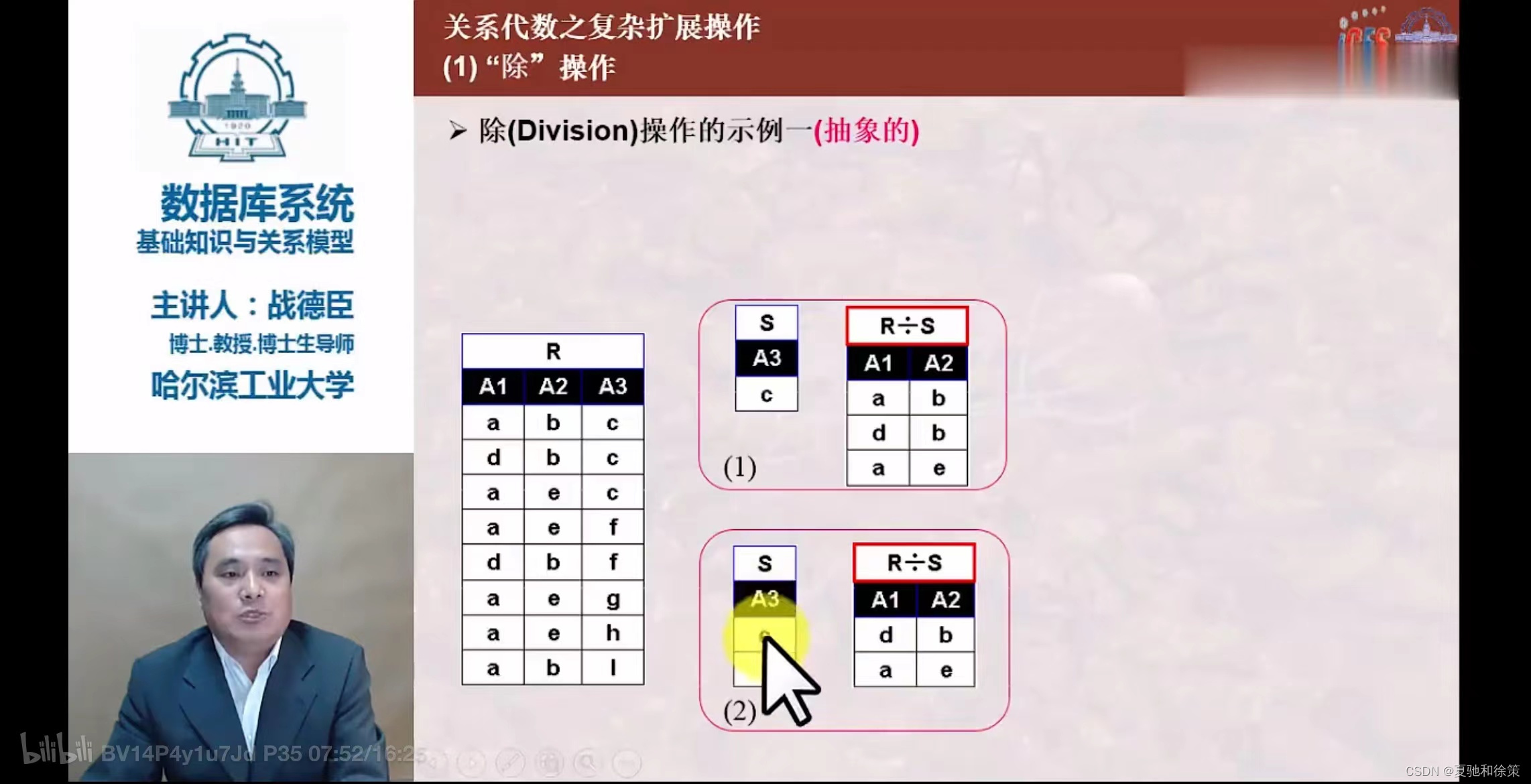
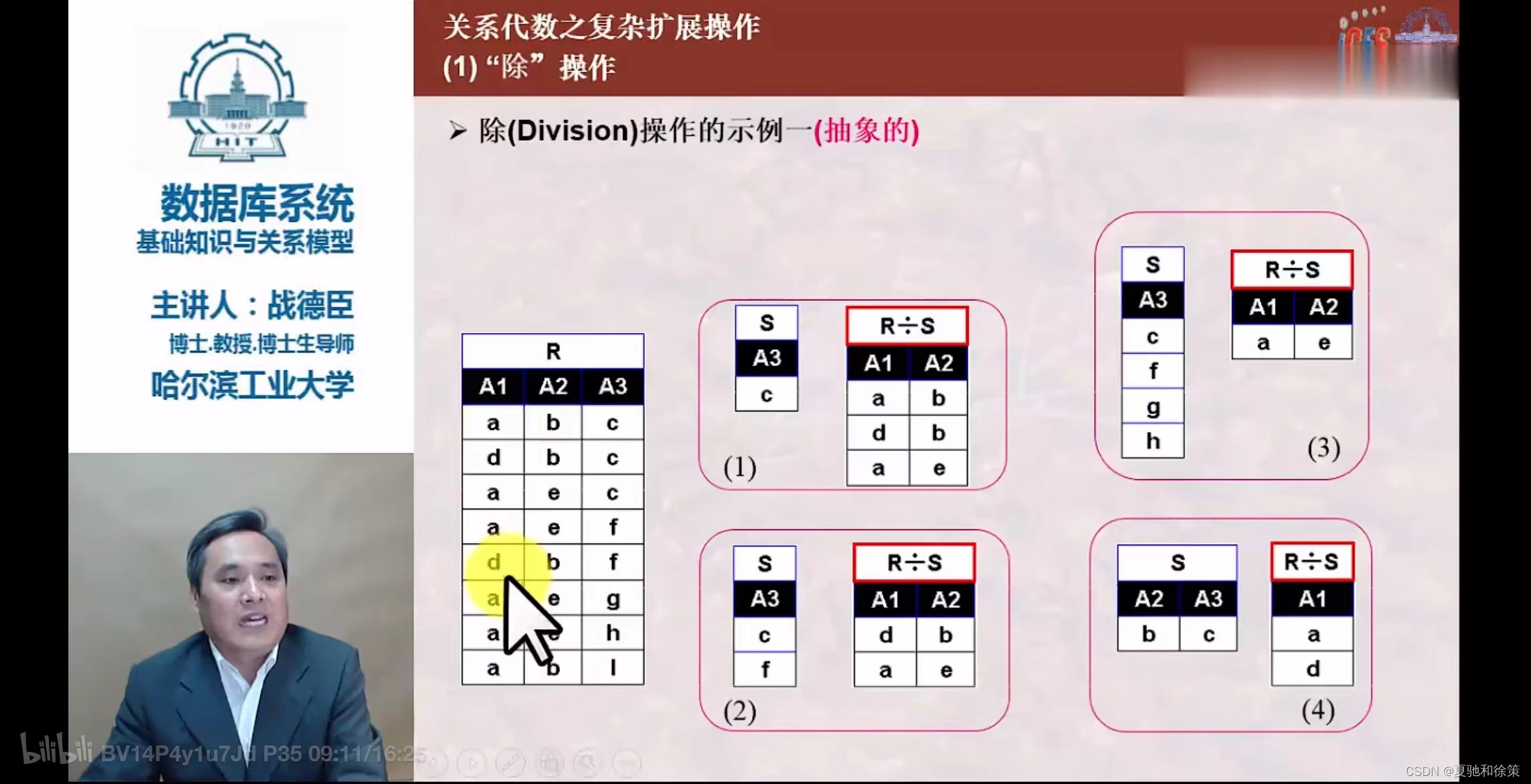
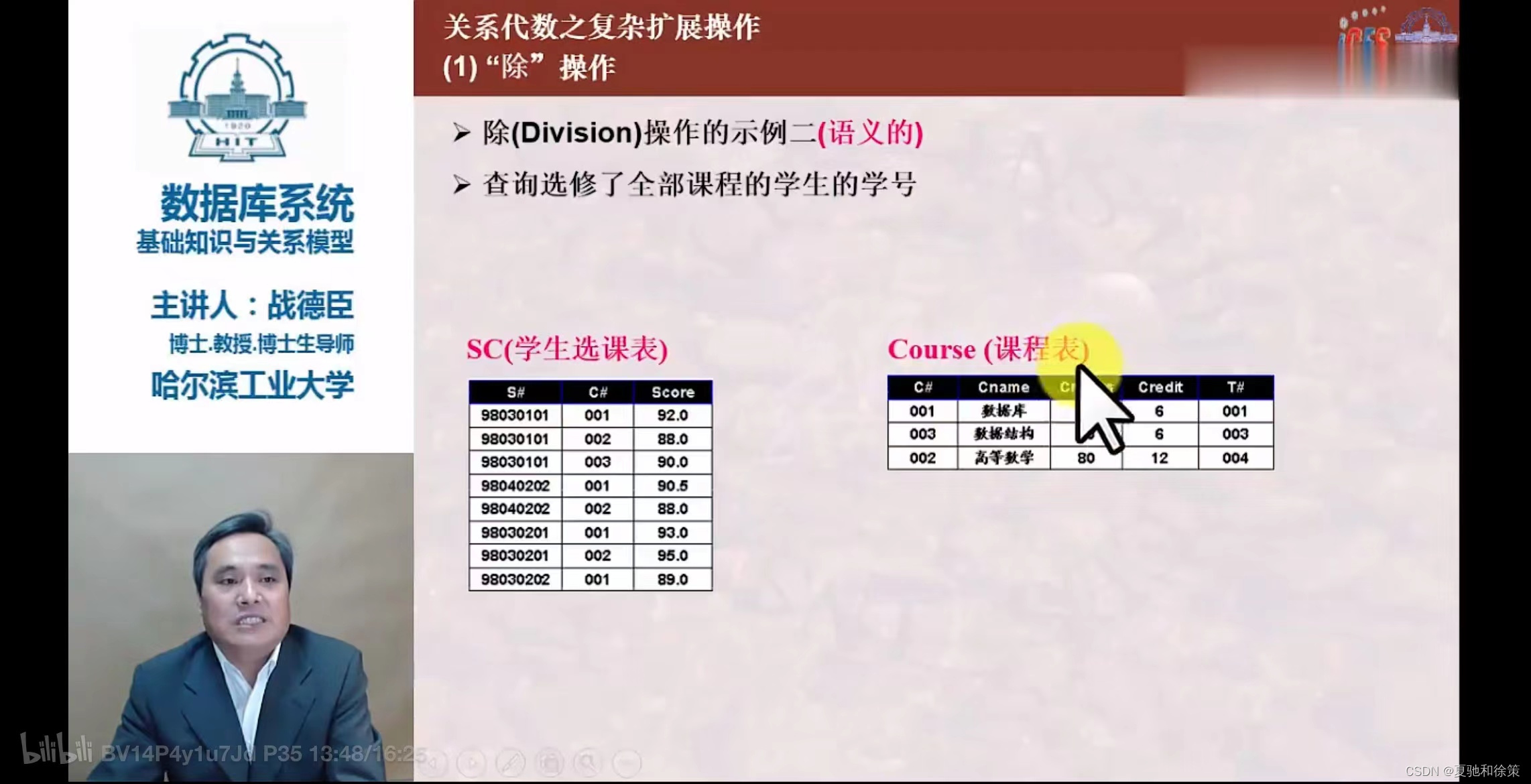
- 设关系 R 除以关系 S 的结果为关系 T，T 包含所有在 R 但不在 S 中的属性及其值。
- T 的元组与 S 的元组的所有组合都在 R 中。
外连接：
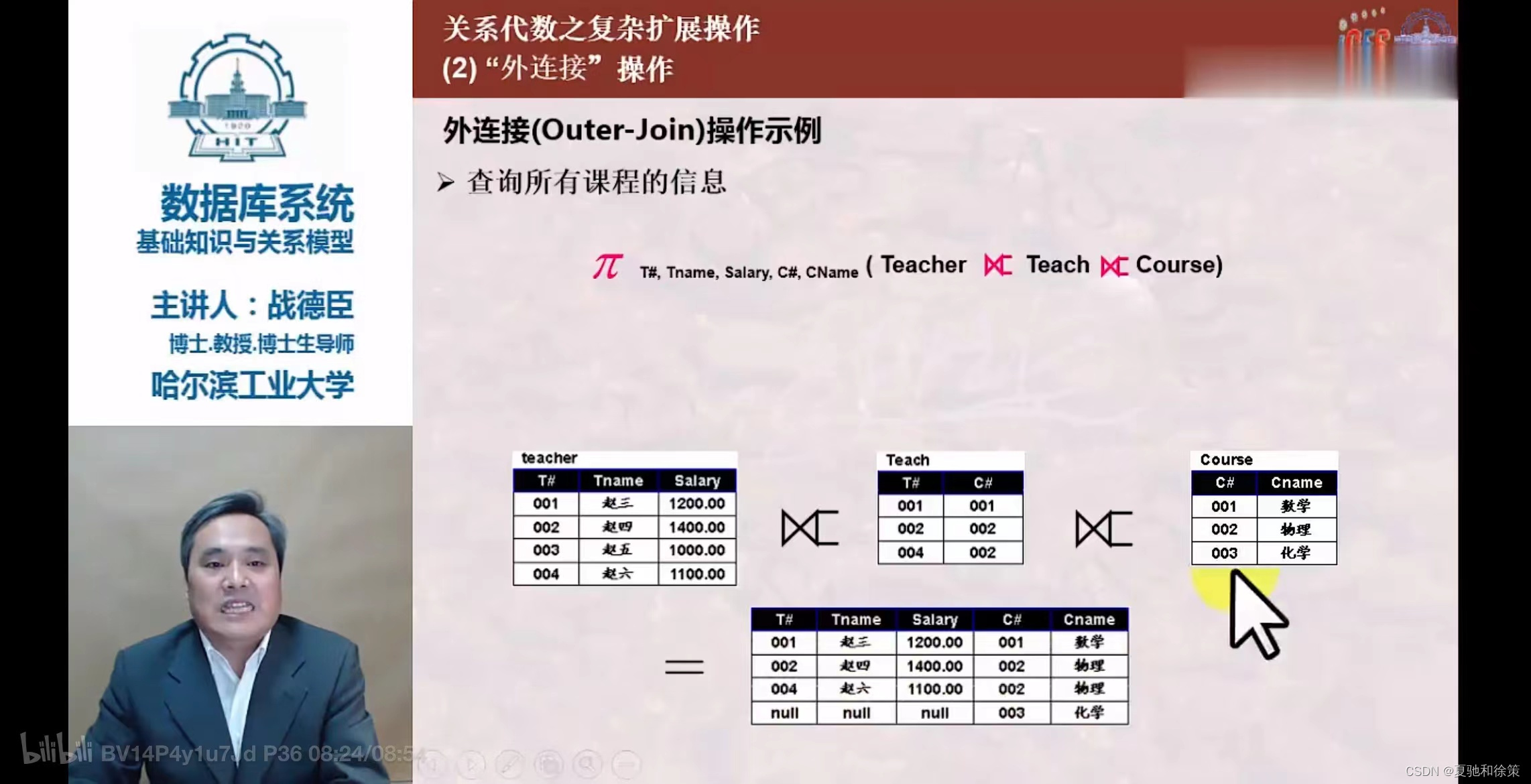
外连接（Outer Join）是数据库中的一种关系运算，用于合并两个表中的记录。它不仅包括符合连接条件的记录，还包括至少一个表中那些不符合连接条件的记录。外连接的主要类型有左外连接（Left Outer Join）、右外连接（Right Outer Join）和全外连接（Full Outer Join）。
左外连接（Left Outer Join）
- 结果集包括左表（第一个表）的所有记录，即使它们在右表（第二个表）中没有匹配的记录。
- 对于左表中的每行，如果在右表中没有匹配，右表中的列将以空值（NULL）填充。
右外连接（Right Outer Join）
- 正好与左外连接相反。
- 结果集包括右表的所有记录，即使它们在左表中没有匹配的记录。
- 对于右表中的每行，如果在左表中没有匹配，左表中的列将以空值（NULL）填充。
全外连接（Full Outer Join）
- 结合了左外连接和右外连接的特点。
- 结果集中包括左表和右表中的所有记录。
- 如果某一侧的行在另一侧没有匹配，则另一侧将以空值填充。

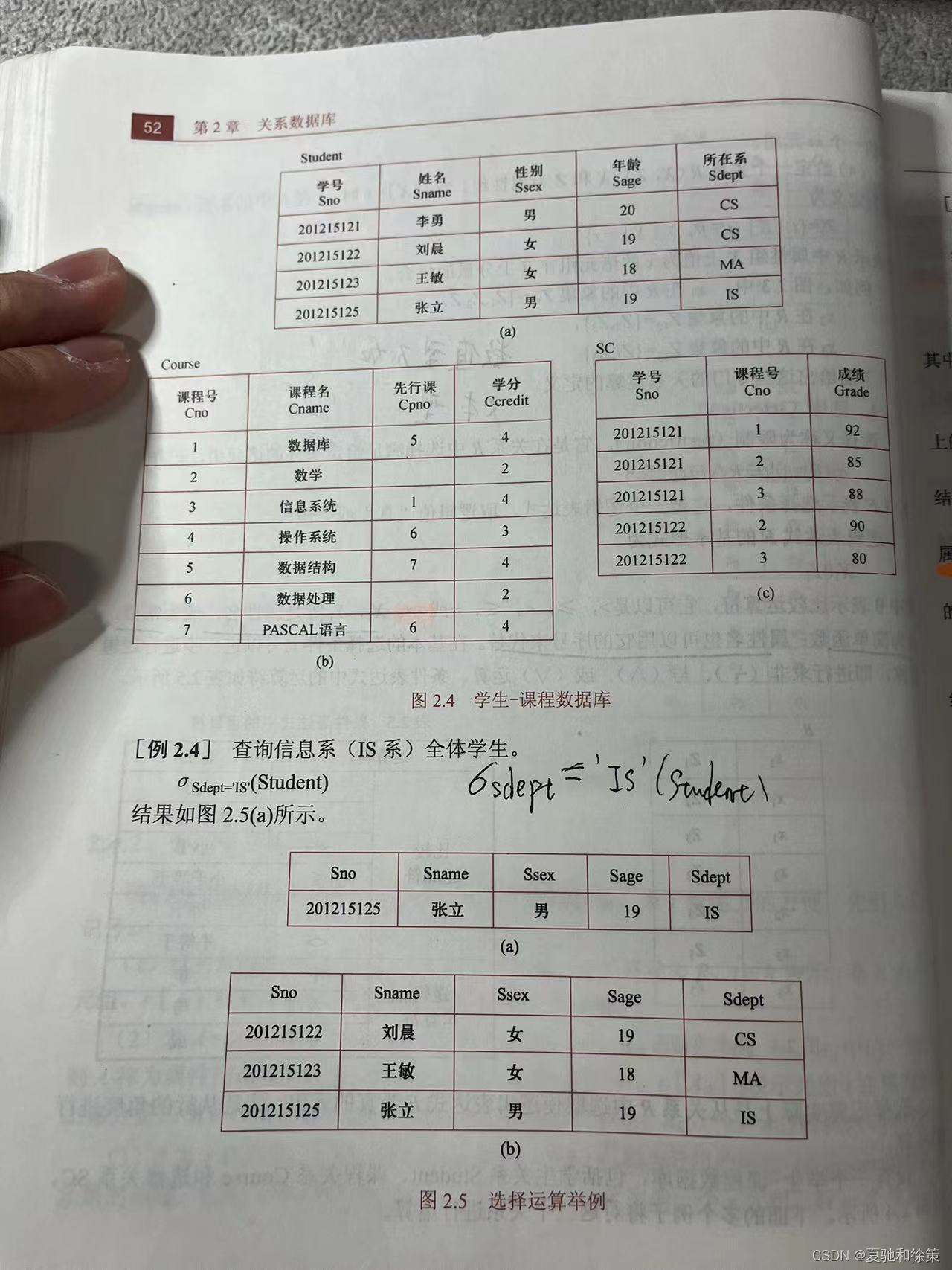
举例

选择运算举例：选择特定条件的元组。
投影运算举例：选择关系中的某些列。
连接运算举例：结合两个关系中满足条件的元组。
除运算举例：找出与另一关系中所有元组均有关联的元组。

结论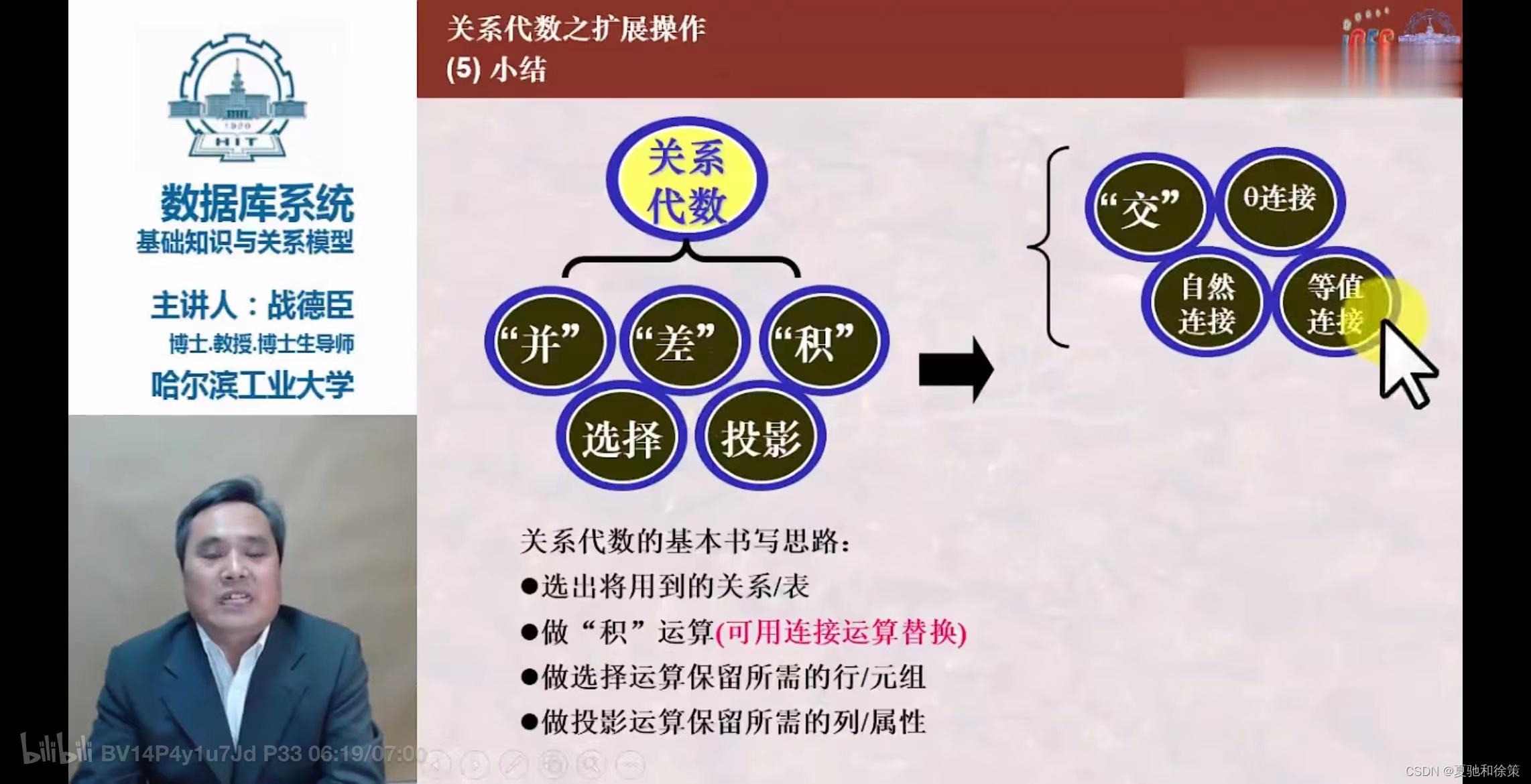

这些运算是关系数据库查询中的核心，提供了从不同角度操作数据的能力。
它们经有限次复合后形成的表达式称为关系代数表达式，是数据库查询语言的基础。

总结：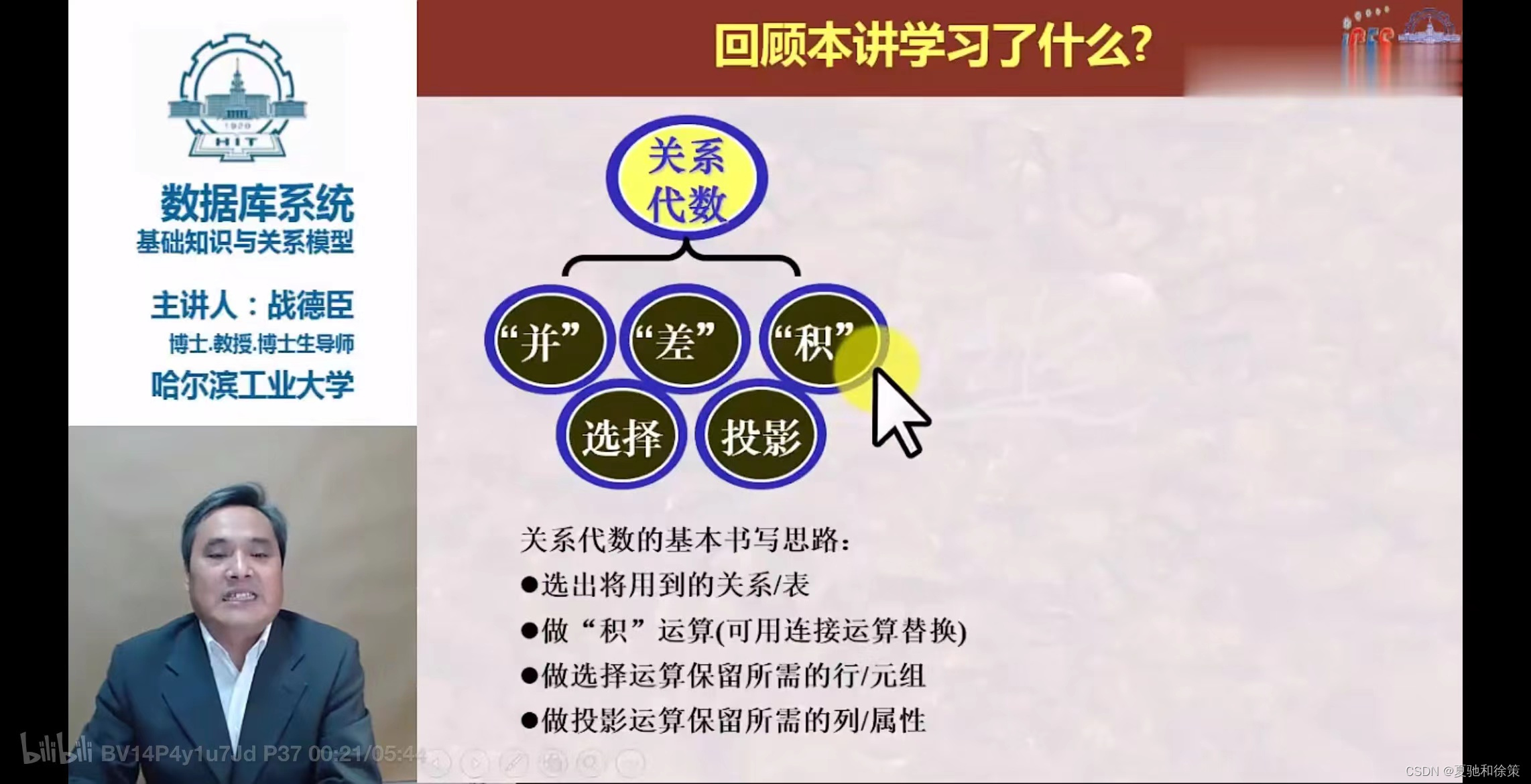

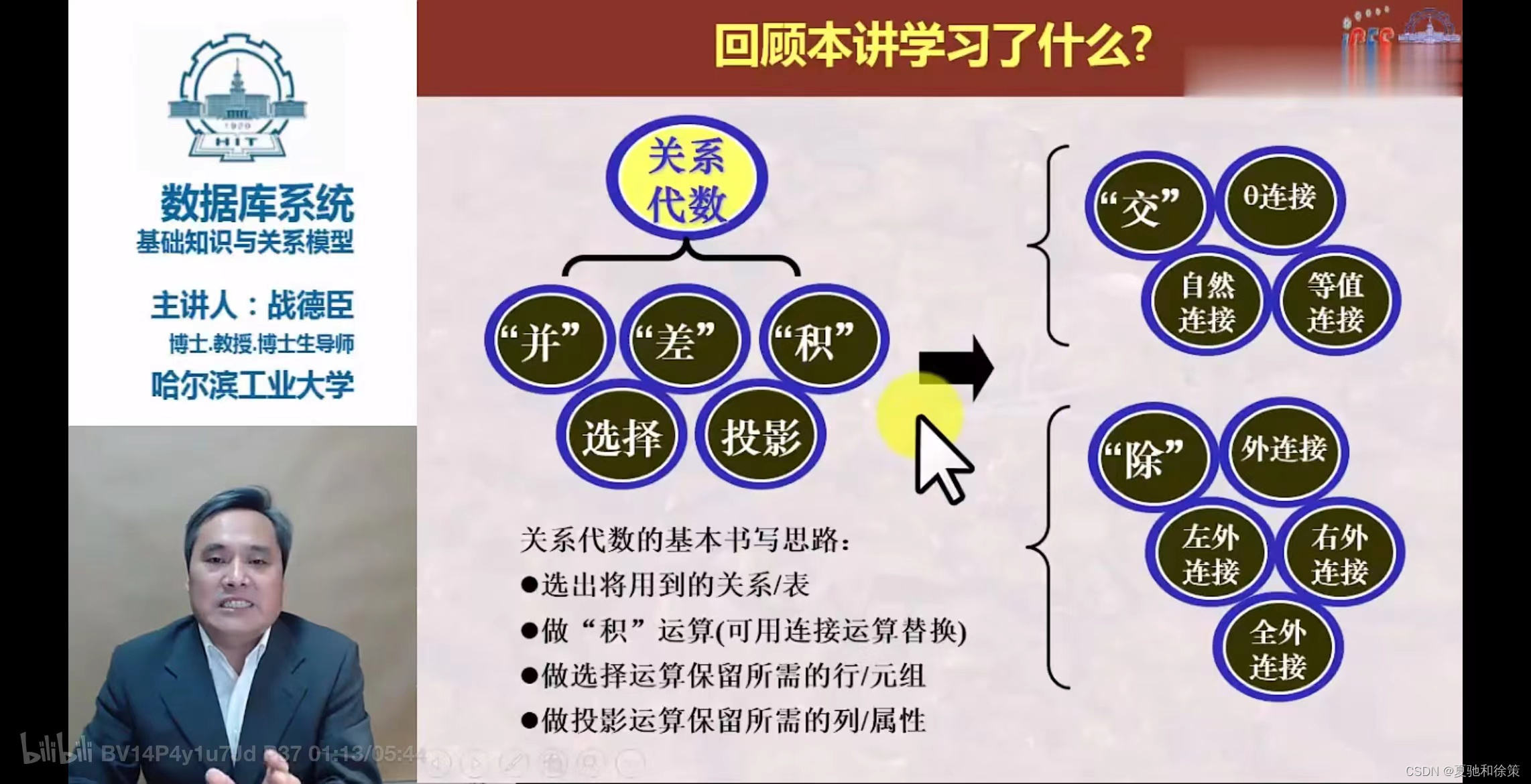
重点

基本概念：关系代数是一种用于描述数据库查询的抽象语言，它涉及对集合（即表格）的操作。
运算类型：包括基本的集合运算（如并、差、交、笛卡尔积）和专门的关系运算（如选择、投影、连接、除）。
集合运算：
- 并（Union）：合并两个结构相同的表。
- 差（Except）：从一个表中排除另一个表的内容。
- 交（Intersection）：两个表的共有部分。
- 笛卡尔积（Cartesian Product）：两个表的所有可能组合。
专门的关系运算：
- 选择（Selection）：基于特定条件筛选行。
- 投影（Projection）：选择一些列，去除其他列。
- 连接（Join）：结合两个表的行。
- 除（Division）：查找与另一个表的所有行都有关联的行。