7.2 可分离变量的微分方程

第二节 可分离变量的微分方程

在本节及接下来的章节中，我们将讨论一阶微分方程 𝑦′=𝑓(𝑥,𝑦)y′=f(x,y) (2-1) 的各种解法。

一阶微分方程有时可以写成对称的形式：

在这种形式中，变量 𝑥x 和 𝑦y 是对称的。此方程可以看作以 𝑥x 为自变量、 𝑦y 为因变量的方程 (当 𝑄(𝑥,𝑦)≠0Q(x,y)=0 时)：

或者可以看作以 𝑦y 为自变量、 𝑥x 为因变量的方程 (当 𝑃(𝑥,𝑦)≠0P(x,y)=0 时)：

1. 可分离变量的示例

在第一节的例 1 中，我们遇到了一阶微分方程：

𝑦′=2𝑥y′=2x

或者表示为：

𝑑𝑦=2𝑥𝑑𝑥dy=2xdx

直接对方程两端积分得到通解：

𝑦=𝑥2+𝐶y=x2+C

然而，并不是所有一阶微分方程都可以直接积分求解。例如，考虑以下方程：

𝑦′=2𝑥𝑦3y′=2xy3 (2-3)

在这里，无法直接对两端积分，因为右侧的表达式同时含有 𝑥x 和 𝑦y 的函数关系。为了使方程易于求解，我们可以通过两端乘以 1𝑦3y31​ 来分离变量，使其变为：

1𝑦3𝑑𝑦=2𝑥𝑑𝑥y31​dy=2xdx

接着，对等式两端进行积分：

−12𝑦2=𝑥2+𝐶−2y21​=x2+C (2-4)

这里， 𝐶C 是任意常数。

可以验证，函数 (2-4) 确实满足微分方程 (2-3)，且含有一个任意常数，因此它是方程 (2-3) 的通解。

2. 一般形式的可分离变量微分方程

一般来说，如果一个一阶微分方程可以写成：

𝑔(𝑦)𝑑𝑦=𝑓(𝑥)𝑑𝑥g(y)dy=f(x)dx (2-5)

也就是说，方程一侧仅包含 𝑦y 和 𝑑𝑦dy 的函数，而另一侧仅包含 𝑥x 和 𝑑𝑥dx 的函数，那么这个方程就称为可分离变量的微分方程。

假定方程 (2-5) 中的函数 𝑔(𝑦)g(y) 和 𝑓(𝑥)f(x) 都是连续的。若 𝑦=𝜙(𝑥)y=ϕ(x) 是方程 (2-5) 的解，将它代入 (2-5) 中可以得到：

对等式两端进行积分，并引入变量 𝑦=𝜙(𝑥)y=ϕ(x)，得：

设 𝐺(𝑦)G(y) 和 𝐹(𝑥)F(x) 分别是 𝑔(𝑦)g(y) 和 𝑓(𝑥)f(x) 的原函数，则：

因此，方程 (2-5) 的解满足关系式 (2-6)。

反过来，如果 𝑦=𝜙(𝑥)y=ϕ(x) 是由关系式 (2-6) 确定的隐函数，那么在 𝑔(𝑦)≠0g(y)=0 的条件下， 𝑦=𝜙(𝑥)y=ϕ(x) 也是方程 (2-5) 的解。通过隐函数求导法可以得出：

这表示函数 𝑦=𝜙(𝑥)y=ϕ(x) 满足方程 (2-5)。

因此，如果已分离变量的方程 (2-5) 中 𝑔(𝑦)g(y) 和 𝑓(𝑥)f(x) 是连续的，并且 𝑔(𝑦)≠0g(y)=0，那么通过对方程两端积分所得到的关系式 (2-6) 就是微分方程 (2-5) 的隐式解。由于该隐式关系含有任意常数，因此它是方程 (2-5) 的通解。

当 𝑓(𝑥)≠0f(x)=0 时，关系式 (2-6) 中确定的隐函数 𝑥=𝜓(𝑦)x=ψ(y) 也可以看作是方程 (2-5) 的解。

第七章 微分方程

例 1: 求微分方程 𝑦′=2𝑥𝑦y′=2xy (2-7) 的通解。

解： 方程 (2-7) 是可分离变量的，分离变量后得：

两端积分：

得到：

从而：

这里， 𝐶C 是任意非零常数，且 𝑦=0y=0 也满足方程 (2-7)。因此，方程 (2-7) 的通解为：

例 2: 放射性元素铀由于不断地放射出微粒子而变成其他元素，铀的含量就不断减少。这种现象称为衰变。已知 𝑡=0t=0 时铀的含量为 𝑀0M0​，求在衰变过程中铀含量 𝑀(𝑡)M(t) 随时间 𝑡t 的变化规律。

解： 铀的衰变速度即 𝑀(𝑡)M(t) 对时间 𝑡t 的导数。由于铀的衰变速度与其含量成正比，因此得到微分方程：

其中 𝐴A ( 𝐴>0A>0 ) 是常数，称为衰变系数。负号是由于 𝑡t 增加时 𝑀M 单调减少。

根据题意，初值条件为：

方程 (2-8) 是可分离变量的。分离变量后得：

两端积分：

以 ln⁡𝐶lnC 表示任意常数，并考虑到 𝑀>0M>0，得到：

即：

这就是方程 (2-8) 的通解。代入初值条件，得到：

所以：

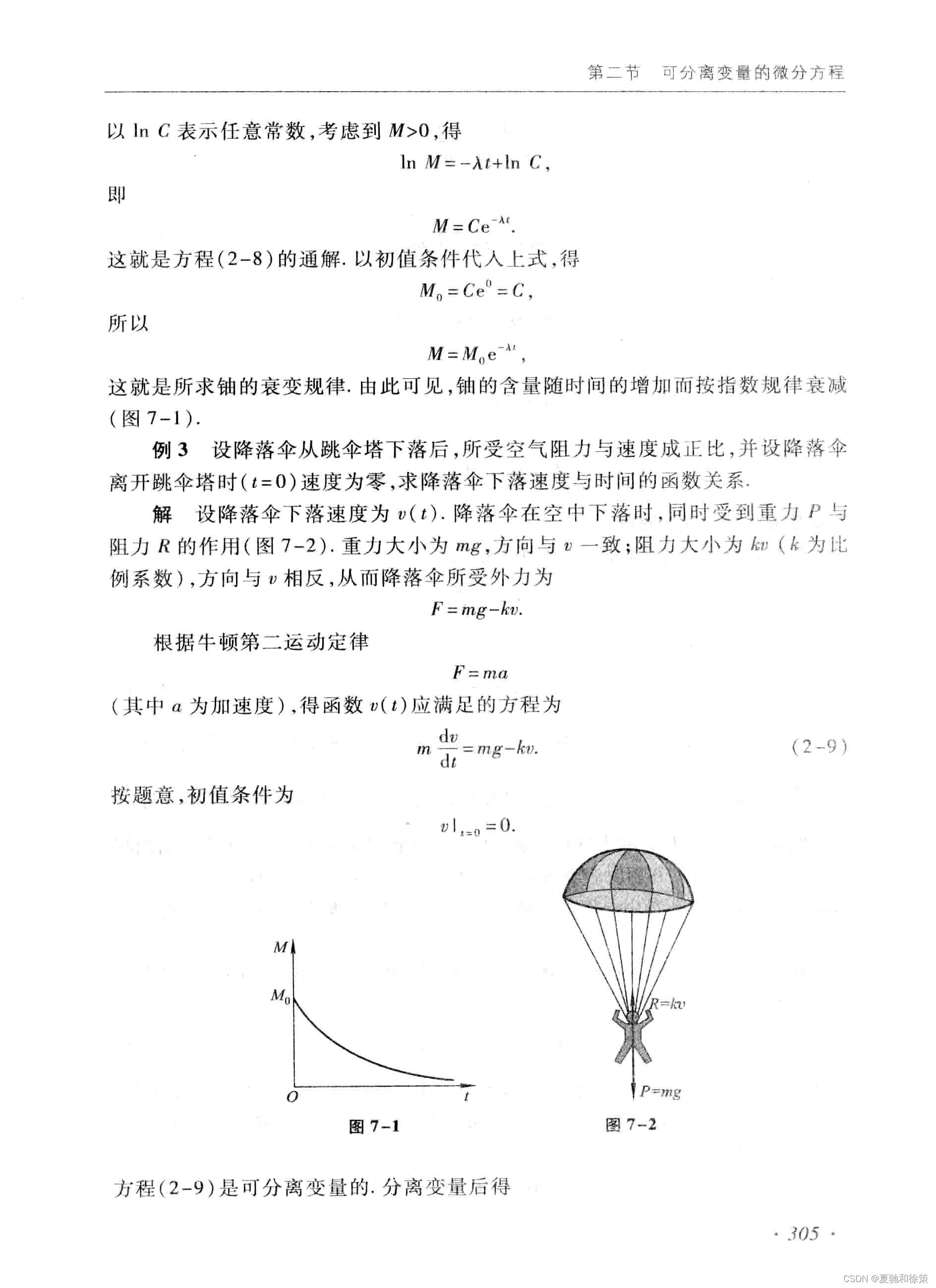
这就是铀的衰变规律。铀的含量随时间呈指数衰减 (图 7-1)。

例 3: 设降落伞从跳伞塔下落后，受到的空气阻力与速度成正比，并设降落伞离开跳伞塔时 ( 𝑡=0t=0 ) 速度为零，求降落伞下落速度与时间的函数关系。

解： 设降落伞的下落速度为 𝑣(𝑡)v(t)。降落伞在空中下落时，受到重力 𝑃P 和阻力 𝑅R 的作用 (图 7-2)。重力大小为 𝑚𝑔mg，方向与 𝑣v 一致；阻力大小为 𝑘𝑣kv ( 𝑘k 为比例系数)，方向与 𝑣v 相反。所以，降落伞所受外力为：

𝐹=𝑚𝑔−𝑘𝑣F=mg−kv

根据牛顿第二运动定律 𝐹=𝑚𝑎F=ma，得到：

𝑚𝑑𝑣𝑑𝑡=𝑚𝑔−𝑘𝑣mdtdv​=mg−kv (2-9)

按题意，初值条件为：

𝑣(0)=0v(0)=0

方程 (2-9) 是可分离变量的。分离变量后得：

𝑚𝑚𝑔−𝑘𝑣𝑑𝑣=𝑑𝑡mg−kvm​dv=dt

两端积分：

∫𝑚𝑚𝑔−𝑘𝑣𝑑𝑣=∫𝑑𝑡∫mg−kvm​dv=∫dt

得到：

考虑到 𝑚𝑔−𝑘𝑣>0mg−kv>0，从而：

解得：

这就是方程 (2-9) 的通解。

将初值条件 𝑣(0)=0v(0)=0 代入 (2-10) 式，得到：

𝐶=1C=1

于是特解为：

从 (2-11) 可以看出，随着时间 𝑡t 的增加，速度 𝑣v 逐渐接近常数 𝑚𝑔𝑘kmg​，但不会超过它。开始阶段降落伞加速下落，但随后逐渐接近等速下落。

例 4: 有高为 1m 的半球形容器，水从底部小孔流出，小孔横截面面积为 1cm² (图 7-3)。开始时容器内盛满了水，求水从小孔流出过程中容器里水面的高度 ℎh 随时间 𝑡t 变化的规律，并求水流完所需的时间。

解： 根据流体力学知识，水从孔口流出的流量 𝑄Q (即通过孔口横截面的水体积 𝑉V 对时间 𝑡t 的变化率) 可以由公式计算：

其中 𝑘k 为流量系数，由实验测得 𝑘=0.62k=0.62； 𝑆S 为孔口横截面面积； 𝑔g 为重力加速度。

另一方面，设在微小时间间隔 [𝑡,𝑡+𝑑𝑡][t,t+dt] 内，水面高度由 ℎh 降至 ℎ+𝑑ℎh+dh ( 𝑑ℎ<0dh<0 )，则可以得到：

其中，𝑟r 是时刻 𝑡t 时的水面半径 (图 7-3)。负号是因为 𝑑ℎ<0dh<0 而 𝑑𝑉>0dV>0。

因为：

𝑟=12−(1−ℎ)2=2ℎ−ℎ2r=12−(1−h)2​=2h−h2​

所以 (2-13) 式变成：

比较 (2-12) 和 (2-14) 式，得到：

这是未知函数 ℎ=ℎ(𝑡)h=h(t) 应满足的微分方程。

此外，开始时容器内水是满的，所以未知函数 ℎ=ℎ(𝑡)h=h(t) 还应满足初值条件：

ℎ(0)=1h(0)=1 (2-16)

方程 (2-15) 是可分离变量的。分离变量后得：

两端积分：

其中，𝐶C 是任意常数。

把初值条件 (2-16) 代入 (2-17) 式，得到：

将 𝐶C 代入 (2-17) 式并化简，得到：

代入 𝑘=0.62k=0.62，𝑆=10−4S=10−4 m²，𝑔=9.8g=9.8 m/s² 计算可得：

上式表达了水从小孔流出过程中容器内水面高度 ℎh 与时间 𝑡t 之间的函数关系。

水完全流出所需的时间为：

𝑡=1.068×104s=2h 58 mint=1.068×104s=2h 58 min

在这个例子中，我们通过对微小量 𝑑𝑉dV 的分析得到了微分方程 (2-15)。这种微小量分析的方法，也是建立微分方程的一种常用方法。