7.6 函数的递归调用

夏驰和徐策

于 2024-05-17 22:33:37 发布

阅读量885

点赞数 23

分类专栏：夏驰和徐策带你从零开始学C语言文章标签：算法 C语言

本文链接：https://blog.csdn.net/tang7mj/article/details/139014032

版权

夏驰和徐策带你从零开始学C语言专栏收录该内容

68 篇文章

订阅专栏

7.6 函数的递归调用

递归调用的概念

在编程中，递归调用是指一个函数在执行过程中直接或间接地调用自身的情况。这是C语言等许多编程语言支持的一种强大功能。递归调用可以分为两类：直接递归和间接递归。直接递归发生时，函数直接调用自身，如下例所示：

int f(int x) {
    int y, z;
    z = f(y);  // 直接调用自身
    return 2 * z;
}

间接递归则涉及两个或多个函数相互调用，例如，函数 f1 调用函数 f2，而 f2 再调用 f1。

递归函数通常需要一个终止条件，以防止无限递归，这通常通过一个或多个 if 语句实现。

递归的实际应用

递归调用在解决问题时非常有用，尤其是那些可以分解为相似子问题的问题。以下是一个实际的例子，说明递归如何应用于解决实际问题。

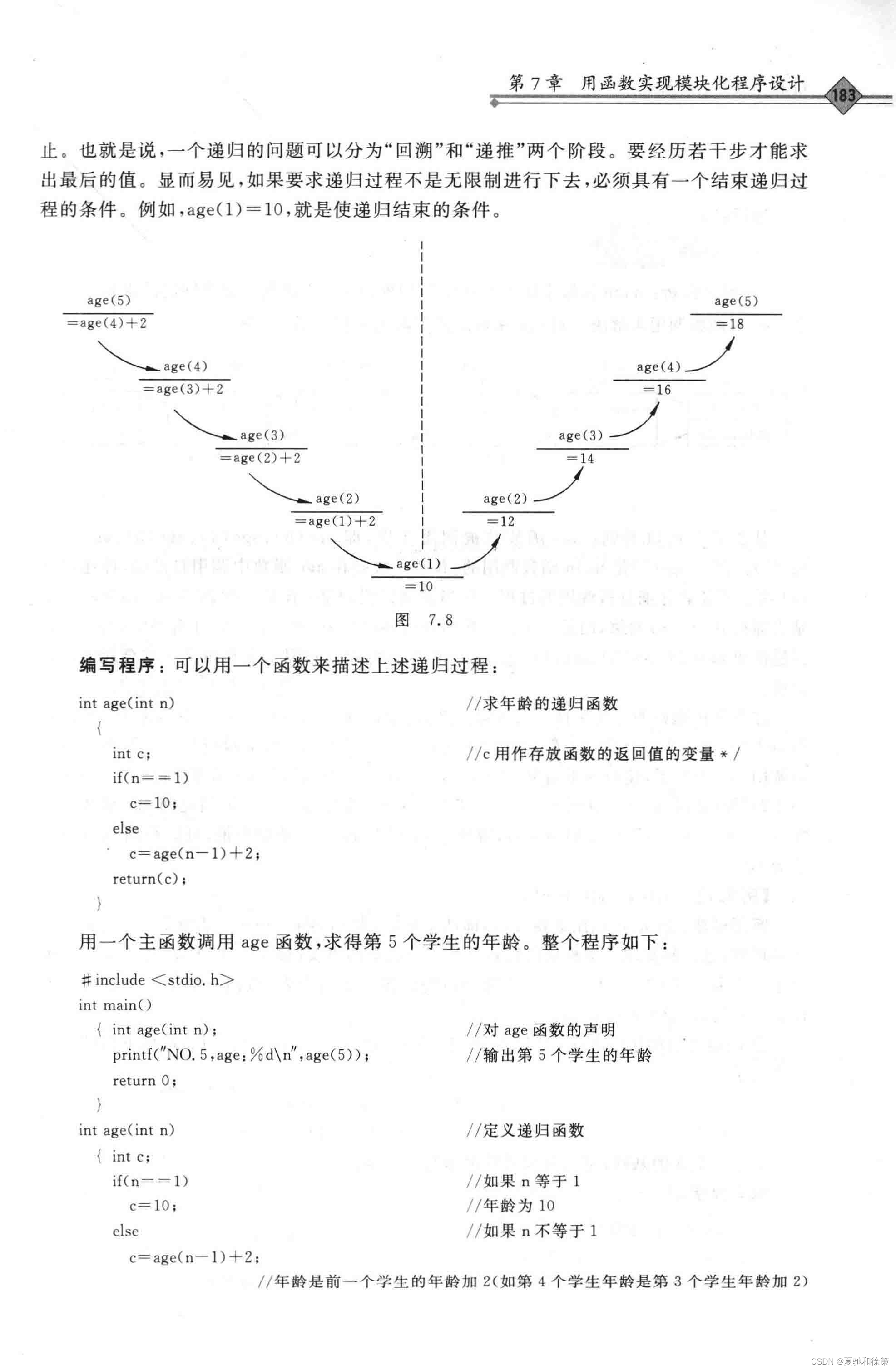
【例7.6】学生的年龄问题

假设有5个学生坐在一起，从第五个学生开始，每个学生的年龄都比前一个学生大2岁。如果知道第一个学生是10岁，可以询问第五个学生的年龄。

这个问题可以通过以下递归函数解决：

#include <stdio.h>

int age(int n);

int main() {
    printf("No. 5 student's age: %d\n", age(5));
    return 0;
}

int age(int n) {
    int c;
    if (n == 1) {
        c = 10;
    } else {
        c = age(n - 1) + 2;
    }
    return c;
}

这个函数首先检查是否达到了递归的基本案例（即 n == 1），如果没有，它会调用自身来求前一个学生的年龄，然后加2。这个过程会一直持续到第一个学生的年龄被直接返回为10岁。

递归过程的分解

回溯阶段：从第五个学生开始，每次递减到前一个学生，直到第一个学生。
递推阶段：从已知的第一个学生的年龄开始，逐步计算出后面每个学生的年龄。

编写程序实现递归

这里是一个C程序，它使用上述递归函数来计算第五个学生的年龄：

#include <stdio.h>

int age(int n);

int main() {
    printf("No. 5 student's age: %d\n", age(5));
    return 0;
}

int age(int n) {
    int c;
    if (n == 1) {
        c = 10;
    } else {
        c = age(n - 1) + 2;
    }
    return c;
}

此程序展示了如何通过一个简单的递归函数解决问题，同时也强调了递归在程序设计中实现模块化的重要性。递归提供了一种优雅的方法来简化代码和逻辑处理，尤其是在处理分层或具有重复性质的数据结构时。

7.6 函数的递归调用

递归调用概述

递归调用是程序设计中一种重要的方法，其中一个函数在执行过程中直接或间接地调用自己。递归调用可以是直接的，如一个函数直接调用其自身，或间接的，如两个或更多的函数相互调用形成闭环。递归方法在解决诸如数学问题、数据分析和算法设计等领域非常有用，因为它可以将复杂的问题分解为更简单的子问题。

递归调用的实例

递归求解阶乘

问题描述

计算阶乘 𝑛!n! 是递归调用的一个经典例子。阶乘的计算通常是通过递推方法完成的，即从 1 开始，逐步乘以 2、3 直至 𝑛n。但使用递归方法，可以将 𝑛!n! 表示为 𝑛×(𝑛−1)!n×(n−1)!，从而简化计算过程。

解题思路

递归解决阶乘问题的基本思路是：如果 𝑛n 大于 1，那么 𝑛!=𝑛×(𝑛−1)!n!=n×(n−1)!；如果 𝑛n 等于 0 或 1，阶乘结果为 1。这种方法首先将问题分解成求 (𝑛−1)!(n−1)!，然后递归求解 (𝑛−1)!(n−1)!，直到达到基本案例。

C 语言实现

#include <stdio.h>

int fac(int n) {
    if (n < 0) {
        printf("n < 0, data error!");
        return -1;  // 处理错误输入
    } else if (n == 0 || n == 1) {
        return 1;  // 递归的基础情况
    } else {
        return n * fac(n - 1);  // 递归调用
    }
}

int main() {
    int n, y;
    printf("Input an integer number: ");
    scanf("%d", &n);
    y = fac(n);
    printf("%d! = %d\n", n, y);
    return 0;
}

在这段代码中，fac 函数是一个递归函数，用于计算并返回 𝑛!n!。主函数 (main) 提供了用户输入和结果展示的界面。