9.9 二元函数的泰勒公式

第九节 二元函数的泰勒公式

一、二元函数的泰勒公式

在上册第三章，我们已经知道：若函数 𝑓(𝑥)f(x) 在 𝑥0x0​ 的某邻域内具有直到 (𝑛+1)(n+1) 阶导数，则对该邻域内的任一 𝑥x，有下面的 𝑛n 阶泰勒公式

利用一元函数的泰勒公式，我们可以用 𝑛n 次多项式来近似表达函数 𝑓(𝑥)f(x)，且误差是当 𝑥→𝑥0x→x0​ 时比 (𝑥−𝑥0)𝑛(x−x0​)n 高阶的无穷小。对于多元函数来说，无论是为了理论的或实际计算的目的，也都有必要考虑用多个变量的多项式来近似表达一个给定的多元函数，并能具体地估算出误差的大小。以二元函数为例，设 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 在点 (𝑥0,𝑦0)(x0​,y0​) 的某一邻域内连续且有 (𝑛+1)(n+1) 阶连续偏导数，(𝑥0+ℎ,𝑦0+𝑘)(x0​+h,y0​+k) 为此邻域内任一点，我们的问题就是要把函数 𝑓(𝑥0+ℎ,𝑦0+𝑘)f(x0​+h,y0​+k) 近似地表达为 ℎ=𝑥−𝑥0h=x−x0​，𝑘=𝑦−𝑦0k=y−y0​ 的 𝑛n 次多项式，而由此所产生的误差是当 𝑝=ℎ2+𝑘2→0p=h2+k2​→0 时比 𝑝𝑛+1pn+1 高阶的无穷小。为了解决这个问题，就要把一元函数的泰勒中值定理推广到多元函数的情形。

定理 设 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 在点 (𝑥0,𝑦0)(x0​,y0​) 的某一邻域内连续且有 (𝑛+1)(n+1) 阶连续偏导数，(𝑥0+ℎ,𝑦0+𝑘)(x0​+h,y0​+k) 为此邻域内任一点，则有

证明 为了利用一元函数的泰勒公式来进行证明，我们引入函数

利用一元函数的麦克劳林公式，得

定理证毕。

公式称为二元函数 𝑓(𝑥,𝑦)f(x,y) 在点 (𝑥0,𝑦0)(x0​,y0​) 的 𝑛n 阶泰勒公式，而 𝑅𝑛Rn​ 的表达式称为拉格朗日余项。

由二元函数的泰勒公式可知，以右端 ℎh 及 𝑘k 的 𝑛n 次多项式近似表达函数 𝑓(𝑥0+ℎ,𝑦0+𝑘)f(x0​+h,y0​+k) 时，其误差为 ∣𝑅𝑛∣∣Rn​∣。由假设，函数的各 (𝑛+1)(n+1) 阶偏导数都连续，故它们的绝对值在点 (𝑥0,𝑦0)(x0​,y0​) 的某一邻域内都不超过某一正常数 𝑀M。于是，有下面的误差估计式：

由此可知，误差 ∣𝑅𝑛∣∣Rn​∣ 是当 𝑝→0p→0 时比 𝑝𝑛+1pn+1 高阶的无穷小。当 𝑛=0n=0 时，公式成为

公式称为二元函数的拉格朗日中值公式。由此可以推得下述结论：

推论 如果函数 𝑓(𝑥,𝑦)f(x,y) 的偏导数 𝑓𝑥(𝑥,𝑦)fx​(x,y)、𝑓𝑦(𝑥,𝑦)fy​(x,y) 在某一区域内都恒等于零，那么函数 𝑓(𝑥,𝑦)f(x,y) 在该区域内为一常数。

例1

求函数 𝑓(𝑥,𝑦)=ln⁡(1+𝑥+𝑦)f(x,y)=ln(1+x+y) 在点 (0,0)(0,0) 的三阶泰勒公式。

解

因为

所以

由三阶泰勒公式得

因此，函数 𝑓(𝑥,𝑦)=ln⁡(1+𝑥+𝑦)f(x,y)=ln(1+x+y) 在点 (0,0)(0,0) 的三阶泰勒公式为

例2

求函数 𝑓(𝑥,𝑦)=𝑒𝑥+𝑦f(x,y)=ex+y 在点 (0,0)(0,0) 的二阶泰勒公式。

解

因为

所以

由二阶泰勒公式得

因此，函数 在点 (0,0)(0,0) 的二阶泰勒公式为

以上就是二元函数泰勒公式的基本理论和应用实例。通过这些例子可以看出，泰勒公式在多元函数的近似计算中有着广泛的应用。

 

二、极值充分条件的证明

下面来证明第八节中的定理2。

设函数 𝑧=𝑓(𝑥,𝑦)z=f(x,y) 在点 𝑃0(𝑥0,𝑦0)P0​(x0​,y0​) 的某邻域 𝑈1(𝑃0)U1​(P0​) 内连续且有一阶及二阶连续偏导数，又 𝑓𝑥(𝑥0,𝑦0)=0fx​(x0​,y0​)=0、𝑓𝑦(𝑥0,𝑦0)=0fy​(x0​,y0​)=0。依二元函数的泰勒公式，对于任一 (𝑥0+ℎ,𝑦0+𝑘)∈𝑈1(𝑃0)(x0​+h,y0​+k)∈U1​(P0​) 有

因 𝑓(𝑥,𝑦)f(x,y) 的二阶偏导数在 𝑈1(𝑃0)U1​(P0​) 内连续，由不等式(9-6)可知，存在点 𝑃0P0​ 的邻域 𝑈2(𝑃0)⊂𝑈1(𝑃0)U2​(P0​)⊂U1​(P0​)，使得对任一 (𝑥0+ℎ,𝑦0+𝑘)∈𝑈2(𝑃0)(x0​+h,y0​+k)∈U2​(P0​) 有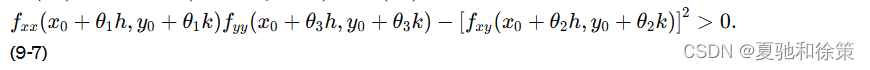

为书写简便起见，把 𝑓𝑥𝑥(𝑥,𝑦)fxx​(x,y)、𝑓𝑥𝑦(𝑥,𝑦)fxy​(x,y)、𝑓𝑦𝑦(𝑥,𝑦)fyy​(x,y) 在点 (𝑥0+𝜃ℎ,𝑦0+𝜃𝑘)(x0​+θh,y0​+θk) 处的值依次记为 𝑓𝑥𝑥fxx​、𝑓𝑥𝑦fxy​、𝑓𝑦𝑦fyy​。由(9-7)式可知，当 (𝑥0+ℎ,𝑦0+𝑘)∈𝑈2(𝑃0)(x0​+h,y0​+k)∈U2​(P0​) 时，𝑓𝑥𝑥fxx​ 及 𝑓𝑦𝑦fyy​ 都不等于零且两者同号。于是(9-5)式可写成

当 ℎ、𝑘h、k 不同时为零且 (𝑥0+ℎ,𝑦0+𝑘)∈𝑈2(𝑃0)(x0​+h,y0​+k)∈U2​(P0​) 时，上式右端方括号内的值为正，所以 Δ𝑓Δf 异于零且与 𝑓𝑥𝑥fxx​ 同号。又由 𝑓(𝑥,𝑦)f(x,y) 的二阶偏导数的连续性知 𝑓𝑥𝑥fxx​ 与 𝐴A 同号，因此 Δ𝑓Δf 与 𝐴A 同号。所以，当 𝐴>0A>0 时，𝑓(𝑥0,𝑦0)f(x0​,y0​) 为极小值，当 𝐴<0A<0 时，𝑓(𝑥0,𝑦0)f(x0​,y0​) 为极大值。

(2)设 𝐴𝐶−𝐵2<0AC−B2<0，

再证 𝑓𝑥𝑥(𝑥0,𝑦0)fxx​(x0​,y0​) 和 𝑓𝑦𝑦(𝑥0,𝑦0)fyy​(x0​,y0​) 不同时为零的情形。不妨假定 𝑓𝑥𝑥(𝑥0,𝑦0)≠0fxx​(x0​,y0​)=0。先取 𝑘=0k=0，于是

但如果取 其中 𝑠s 是异于零但充分接近零的数，则可发现，当 ∣𝑠∣∣s∣ 充分小时，Δ𝑓Δf 与 𝑓𝑥𝑥(𝑥0,𝑦0)fxx​(x0​,y0​) 异号。事实上，在(9-5)式中将 ℎh 及 𝑘k 用(9-9)式给定的值代入，得

上式右端花括号内的式子当 𝑠→0s→0 时趋于极限 𝑓𝑥𝑥(𝑥0,𝑦0)𝑓𝑦𝑦(𝑥0,𝑦0)−[𝑓𝑥𝑦(𝑥0,𝑦0)]2fxx​(x0​,y0​)fyy​(x0​,y0​)−[fxy​(x0​,y0​)]2。由不等式(9-8)，上式花括号内的值为负，因此当 𝑠s 充分接近零时，(9-10)式右端从而 Δ𝑓Δf 与 𝑓𝑥𝑥(𝑥0,𝑦0)fxx​(x0​,y0​) 异号。

以上已经证得：在点 (𝑥0,𝑦0)(x0​,y0​) 的任意邻近，Δ𝑓Δf 可取不同符号的值，因此 𝑓(𝑥0,𝑦0)f(x0​,y0​) 不是极值。

(3)考察函数

容易验证，这两个函数都以 (0,0)(0,0) 为驻点，且在点 (0,0)(0,0) 处都满足 𝐴𝐶−𝐵2=0AC−B2=0。但 𝑓(𝑥,𝑦)f(x,y) 在点 (0,0)(0,0) 处有极小值，而 𝑔(𝑥,𝑦)g(x,y) 在点 (0,0)(0,0) 处却没有极值。

以上即为极值充分条件的证明。