8.13.11 ACM-ICPC 多项式与生成函数符号化方法

本文链接：https://blog.csdn.net/tang7mj/article/details/139468134

8.13.11 ACM-ICPC 多项式与生成函数

符号化方法

符号化方法（symbolic method）是将组合对象快速转换成生成函数的一种方法，我们将考虑对于集合上定义的特定运算，然后导出其对应的生成函数的运算。

我们称一个组合类（或简称为类）为 (A,∣⋅∣)(\mathcal{A}, |\cdot|)(A,∣⋅∣)，其中 A\mathcal{A}A 为组合对象的集合，函数 ∣⋅∣|\cdot|∣⋅∣ 将每一个组合对象映射为一个非负整数，一般称为大小函数。需要注意的是这个非负整数不能是无限大的。例如，对于字符集为 {0,1}\{0,1\}{0,1} 的字符串，可以将字符串的长度设置为其大小函数；对于树或图可将节点的数量设置为其大小函数，注意这并非绝对，也可能将某些特定节点的大小函数设置为 0 等。

本文是基于 Analytic Combinatorics 一书第一章的简化。

无标号体系

在无标号体系中将使用普通生成函数（OGF）。对于集合 A\mathcal{A}A 其对应 OGF 记为

我们约定使用同一组的字母表示同一个类对应的生成函数等，例如用 ana_nan 表示 [zn]A(z)[z^n]A(z)[zn]A(z) 即 A(z)A(z)A(z) 中 znz^nzn 的系数，用 An\mathcal{A}_nAn 表示 A\mathcal{A}A 中大小函数为 nnn 的对象的集合（所以 an=card⁡(An)a_n = \operatorname{card}(\mathcal{A}_n)an=card(An) 其中 card⁡\operatorname{card}card 为基数（cardinality））。

本文将不讨论可容许性（admissibility），读者可参考文献中的内容。

下面将引入两种特殊的组合类和组合对象：

记 ϵ\epsilonϵ 为中性对象（neutral object）和 E={ϵ}\mathcal{E} = \{\epsilon\}E={ϵ} 为中性类（neutral class），中性对象的大小为 0，中性类的 OGF 为 E(z)=1E(z) = 1E(z)=1。
记 ∘\circ∘ 或 ∙\bullet∙ 为原子对象（atom object）和 Z∘={∘}\mathcal{Z}_{\circ} = \{\circ\}Z∘={∘} 或 Z∙={∙}\mathcal{Z}_{\bullet} = \{\bullet\}Z∙={∙} 或简写为 Z\mathcal{Z}Z 为原子类（atom class），原子对象的大小为 1，原子类的 OGF 为 Z(z)=zZ(z) = zZ(z)=z。

对于两个组合类 A\mathcal{A}A 和 B\mathcal{B}B 在组合意义上同构记为 A=B\mathcal{A} = \mathcal{B}A=B 或 A≅B\mathcal{A} \cong \mathcal{B}A≅B，但仅当该同构不平凡时才使用后者的记号。

我们有

其中 ×\times× 为二元运算，表示集合的笛卡尔积。

集合的（不相交）并构造

对于类 A\mathcal{A}A 和 B\mathcal{B}B 的并记为

如此定义可以不违背集合论中集合不相交的要求，我们可以想象成将 A\mathcal{A}A 中的对象染色成红色，将 B\mathcal{B}B 中的对象染色成蓝色。

对应 OGF 为

A(z)+B(z)A(z) + B(z)A(z)+B(z)

考虑

对应形式幂级数的加法。

集合的笛卡尔积构造

对于类 A\mathcal{A}A 和 B\mathcal{B}B 的笛卡尔积记为

A×B={(α,β)∣α∈A,β∈B}\mathcal{A} \times \mathcal{B} = \{ (\alpha, \beta) \mid \alpha \in \mathcal{A}, \beta \in \mathcal{B} \}A×B={(α,β)∣α∈A,β∈B}

对应 OGF 为

A(z)⋅B(z)A(z) \cdot B(z)A(z)⋅B(z)

我们定义 (α,β)(\alpha, \beta)(α,β) 的大小为其组成部分的大小之和，那么显然也有

所以

对应形式幂级数的乘法。

集合的 Sequence 构造

Sequence 构造生成了所有可能的组合。

例子

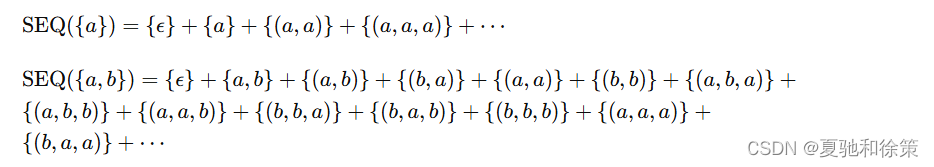
可以看到 {(a,b)},{(b,a)}\{(a,b)\}, \{(b,a)\}{(a,b)},{(b,a)} 这样组成部分的顺序不同的元素被生成了，可以认为 Sequence 构造生成了有序的组合。

我们定义

且要求 A0=∅\mathcal{A}_0 = \varnothingA0=∅，也就是 A\mathcal{A}A 中没有大小为 0 的对象。

对应 OGF 为

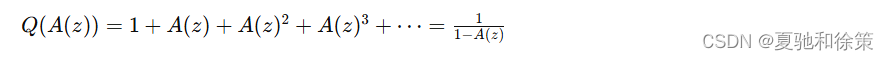
其中 QQQ 为 Pólya 准逆（quasi-inversion）。

集合的 Multiset 构造

Multiset 构造生成了所有可能的组合，但不区分组成部分的元素之间的顺序。

例子

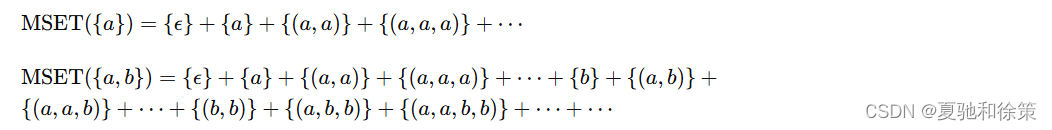
注意到 {(b,a)},{(a,b,a)}\{(b,a)\}, \{(a,b,a)\}{(b,a)},{(a,b,a)} 在 SEQ⁡({a,b})\operatorname{SEQ}(\{a,b\})SEQ({a,b}) 中出现，但在 MSET⁡({a,b})\operatorname{MSET}(\{a,b\})MSET({a,b}) 没有出现，可以认为 Multiset 生成了无序的组合。

我们定义其递推式为

即

且要求 A0=∅\mathcal{A}_0 = \varnothingA0=∅。或者也可以给出等价的

其中 R\mathbf{R}R 为等价关系，我们说 (α1,…,αn)R(β1,…,βn)(\alpha_1, \dots, \alpha_n) \mathbf{R} (\beta_1, \dots, \beta_n)(α1,…,αn)R(β1,…,βn) 当且仅当存在任一置换 σ\sigmaσ 对于所有 jjj 满足 βj=ασ(j)\beta_j = \alpha_{\sigma(j)}βj=ασ(j)。

对应 OGF 为

注意到

其中 Exp⁡\operatorname{Exp}Exp 为 Pólya 指数，也被称为 Euler 变换。

例题

例题 LOJ 6268. 分拆数

题意：令 f(n)f(n)f(n) 表示将 nnn 进行分拆的方案数，求 f(1),f(2),…,f(105)f(1), f(2), \dots, f(10^5)f(1),f(2),…,f(105) 对 998244353 取模的值。

解：设全体正整数类为 I\mathcal{I}I，那么 I=SEQ⁡≥1(Z)=Z×SEQ⁡(Z)\mathcal{I} = \operatorname{SEQ}_{\geq 1}(\mathcal{Z}) = \mathcal{Z} \times \operatorname{SEQ}(\mathcal{Z})I=SEQ≥1(Z)=Z×SEQ(Z)（下标 ≥1\geq 1≥1 为有限制的构造，见后文）。所求即

MSET⁡(I)\operatorname{MSET}(\mathcal{I})MSET(I)

对应 OGF 前几项系数为 1, 2, 3, 5, 7, 11, 15, 22, 30, 42（忽略常数项）即 OEIS A000041。

例题洛谷 P4389 付公主的背包

题意：给出 nnn 种体积分别为 v1,…,vnv_1, \dots, v_nv1,…,vn 的商品和正整数 mmm，求体积为 1, 2, \dots, m 的背包装满的方案数（商品数量不限，有同体积的不同种商品）对 998244353 取模的值。约定 1≤n,m≤1051 \leq n, m \leq 10^51≤n,m≤105 且 1≤vi≤m1 \leq v_i \leq m1≤vi≤m。

解：设商品的组合类为 A\mathcal{A}A，所求即 MSET⁡(A)\operatorname{MSET}(\mathcal{A})MSET(A) 对应 OGF 的系数。

例题洛谷 P5900 无标号无根树计数

题意：求出 nnn 个节点的无标号无根树的个数对 998244353 取模的值。约定 1≤n≤2×1051 \leq n \leq 2 \times 10^51≤n≤2×105。

解：设无标号有根树的组合类为 T\mathcal{T}T，那么

T={∙}×MSET⁡(T)\mathcal{T} = \{\bullet\} \times \operatorname{MSET}(\mathcal{T})T={∙}×MSET(T)

根据 Richard Otter 的论文 The Number of Trees 中的描述，对应无根树的 OGF 为

T(z)−12T2(z)+12T(z2)T(z) - \frac{1}{2}T^2(z) + \frac{1}{2}T(z^2)T(z)−21T2(z)+21T(z2)

前几项系数为 1, 1, 1, 2, 3, 6, 11, 23, 47, 106（忽略常数项）即 OEIS A000055。