8.13.12 ACM-ICPC 多项式与生成函数 Lagrange 反演

8.13.12 ACM-ICPC 多项式与生成函数：Lagrange 反演

在 ACM-ICPC 等算法竞赛中，多项式与生成函数是非常重要的工具，而 Lagrange 反演公式则是其中一个强有力的方法。Lagrange 反演公式主要用于解决某些复杂的组合计数问题，其核心思想是通过逆函数来求解给定方程的解的数目。本文将详细介绍 Lagrange 反演公式的定义、推导过程及其在竞赛中的应用。

形式 Laurent 级数

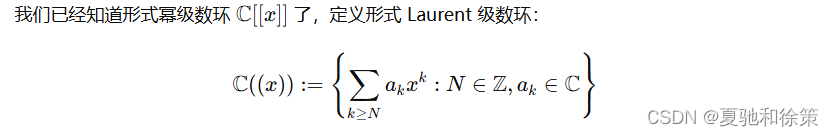
我们可以仿照形式幂级数的乘法逆元定义来定义 C((x))\mathbb{C}((x))C((x)) 上元素的乘法逆元：

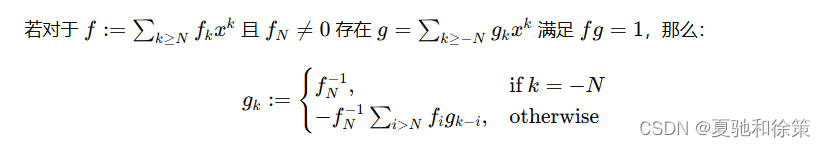
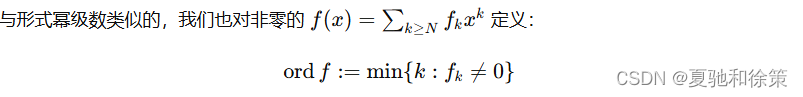
显然对于 g≠0g \neq 0g=0 有：

形式留数

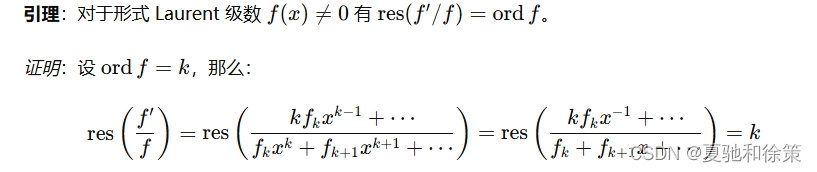
引理：对于形式 Laurent 级数 fff 和形式幂级数 g≠0g \neq 0g=0 有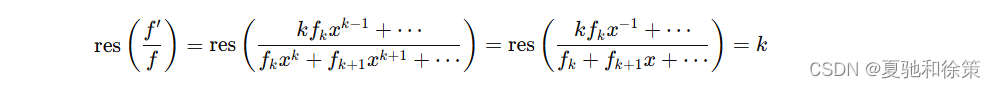

证明：考虑线性性，我们只需证明 f=xkf = x^kf=xk 其中 k∈Zk \in \mathbb{Z}k∈Z 的情况即可，若 k≠−1k \neq -1k=−1 那么：

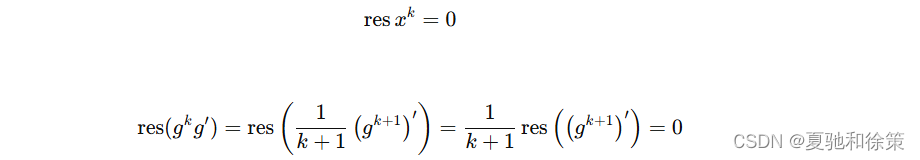
若 k=−1k = -1k=−1 那么：

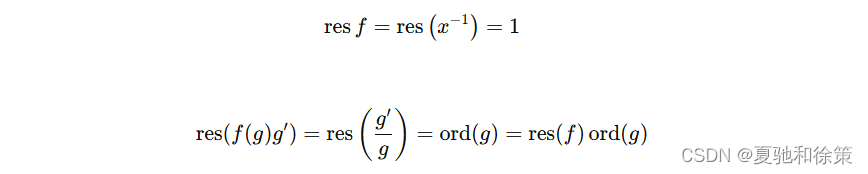
复合逆

命题：f(x):=∑k≥1fkxkf(x) := \sum_{k \geq 1} f_k x^kf(x):=∑k≥1​fk​xk 存在复合逆 f〈−1〉(x)f^{\langle -1 \rangle}(x)f〈−1〉(x) 当且仅当 f(0)=0≠f′(0)f(0) = 0 \neq f'(0)f(0)=0=f′(0)，此时 f〈−1〉(x)f^{\langle -1 \rangle}(x)f〈−1〉(x) 是唯一的。进一步说：若 g(x)=∑k≥1gkxkg(x) = \sum_{k \geq 1} g_k x^kg(x)=∑k≥1​gk​xk 满足 f(g(x))=xf(g(x)) = xf(g(x))=x 或 g(f(x))=xg(f(x)) = xg(f(x))=x 那么 g(x)=f〈−1〉(x)g(x) = f^{\langle -1 \rangle}(x)g(x)=f〈−1〉(x)。

证明：考虑

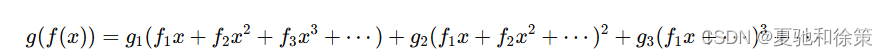
因为 g(f(x))=xg(f(x)) = xg(f(x))=x 所以有下面的方程组：

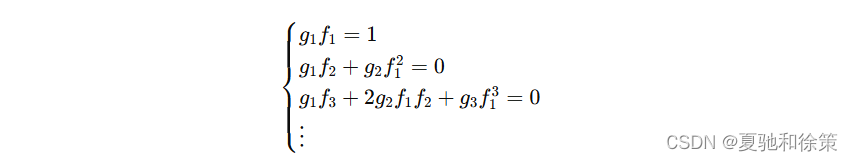
我们只能在 f1≠0f_1 \neq 0f1​=0 时才能解出第一个等式，然后依次可以解出 g2,…g_2, \ldotsg2​,…。

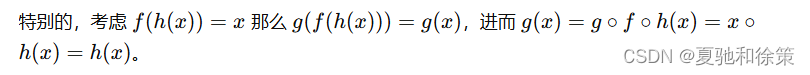
Lagrange 反演公式

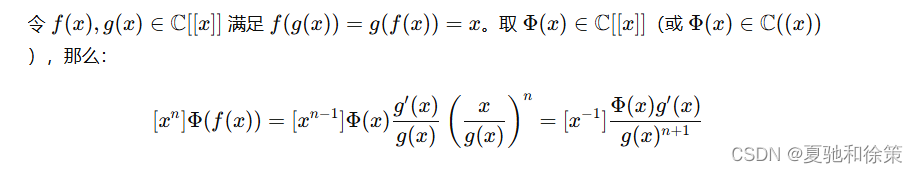
证明：

 

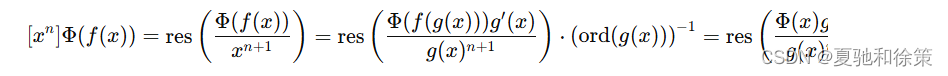
一些读者可能会更加熟悉下面的版本：对于 k∈Z≥0,n∈Z>0k \in \mathbb{Z}_{\geq 0}, n \in \mathbb{Z}_{>0}k∈Z≥0​,n∈Z>0​ 有：

可以通过我们已经证明的部分导出。

应用示例

例 1：Catalan 数

Catalan 数是组合数学中的重要数列，定义为满足以下递推关系的数列：

其生成函数为：

根据定义，可以得到以下方程：

利用 Lagrange 反演公式，可以求解 Catalan 数的具体形式。假设 f(y)=1+y2f(y) = 1 + y^2f(y)=1+y2，则有：

通过展开，可以得到 Catalan 数的通项公式：

例 2：树的计数

给定 nnn 个节点的树的生成函数 T(x)T(x)T(x)，满足以下方程：

利用 Lagrange 反演公式，可以求解 nnn 个节点的树的数量。假设 f(y)=eyf(y) = e^yf(y)=ey，则有：

由于 enye^{ny}eny 的级数展开很简单，可以直接计算出：

这就是著名的 Cayley 公式，用于计算 nnn 个节点的树的数量。

总结

Lagrange 反演公式是组合数学中的重要工具，尤其在算法竞赛中具有重要应用。通过理解公式的定义和推导过程，可以更好地解决复杂的组合计数问题。希望本文能够帮助读者更好地理解和应用 Lagrange 反演公式，提高算法竞赛中的解决问题的能力。