
8.14.8 ACM-ICPC 组合数学 斯特林数
引言
斯特林数(Stirling Numbers)是组合数学中的一个重要概念,用于解决一些特殊的组合问题。斯特林数主要分为第一类斯特林数和第二类斯特林数,两者在不同的组合问题中有广泛的应用。本节将详细介绍斯特林数的定义、性质以及应用。
第一类斯特林数
第一类斯特林数 S(n,k)S(n, k)S(n,k) 表示将 nnn 个元素的集合划分为 kkk 个非空循环排列的方式数。其递推公式为:
S(n,k)=S(n−1,k−1)+(n−1)S(n−1,k)S(n, k) = S(n-1, k-1) + (n-1)S(n-1, k)S(n,k)=S(n−1,k−1)+(n−1)S(n−1,k)
其中,边界条件为:
S(0,0)=1S(0, 0) = 1S(0,0)=1 S(n,0)=0 (n>0)S(n, 0) = 0 \, (n > 0)S(n,0)=0(n>0) S(0,k)=0 (k>0)S(0, k) = 0 \, (k > 0)S(0,k)=0(k>0)
第二类斯特林数
第二类斯特林数 S(n,k)S(n, k)S(n,k) 表示将 nnn 个元素的集合划分为 kkk 个非空子集的方式数。其递推公式为:
S(n,k)=kS(n−1,k)+S(n−1,k−1)S(n, k) = kS(n-1, k) + S(n-1, k-1)S(n,k)=kS(n−1,k)+S(n−1,k−1)
其中,边界条件为:
S(0,0)=1S(0, 0) = 1S(0,0)=1 S(n,0)=0 (n>0)S(n, 0) = 0 \, (n > 0)S(n,0)=0(n>0) S(0,k)=0 (k>0)S(0, k) = 0 \, (k > 0)S(0,k)=0(k>0)
性质
斯特林数具有许多有趣的性质和应用,以下是其中一些主要性质:
-
对称性:第二类斯特林数具有对称性,满足以下关系:
S(n,k)=S(n,n−k)S(n, k) = S(n, n-k)S(n,k)=S(n,n−k)
-
生成函数:第二类斯特林数的生成函数为:
∑k=0nS(n,k)xk=x(x+1)(x+2)⋯(x+n−1)\sum_{k=0}^{n} S(n, k) x^k = x(x+1)(x+2) \cdots (x+n-1)∑k=0nS(n,k)xk=x(x+1)(x+2)⋯(x+n−1)
-
贝尔数:将 nnn 个元素划分成任意数量的非空子集的总数为 BnB_nBn,称为第 nnn 个贝尔数:
Bn=∑k=0nS(n,k)B_n = \sum_{k=0}^{n} S(n, k)Bn=∑k=0nS(n,k)
应用
斯特林数在许多组合问题中都有应用,以下是几个典型的例子:
- 划分问题:将 nnn 个元素划分为 kkk 个非空子集的方式数,即为第二类斯特林数 S(n,k)S(n, k)S(n,k)。
- 排列问题:将 nnn 个元素划分为 kkk 个非空循环排列的方式数,即为第一类斯特林数 S(n,k)S(n, k)S(n,k)。
- 贝尔数:计算 nnn 个元素的所有划分方式数,即为第 nnn 个贝尔数。
实例分析
以下是一个使用第二类斯特林数解决划分问题的例子:
def stirling_number_2nd(n, k):
if n == 0 and k == 0:
return 1
if n == 0 or k == 0:
return 0
dp = [[0 for _ in range(k+1)] for _ in range(n+1)]
dp[0][0] = 1
for i in range(1, n+1):
for j in range(1, k+1):
dp[i][j] = j * dp[i-1][j] + dp[i-1][j-1]
return dp[n][k]
# 计算 S(5, 3)
n, k = 5, 3
print(f"第二类斯特林数 S({n}, {k}) = {stirling_number_2nd(n, k)}")
输出结果:
第二类斯特林数 S(5, 3) = 25
总结
斯特林数是组合数学中的一个重要概念,广泛应用于划分问题和排列问题。通过掌握斯特林数的定义、性质和应用,可以更好地解决 ACM-ICPC 竞赛中的组合数学问题。在实际应用中,递归和动态规划是计算斯特林数的两种主要方法。
引言
斯特林数(Stirling Numbers)是组合数学中的一个重要概念,用于解决一些特殊的组合问题。斯特林数主要分为第一类斯特林数和第二类斯特林数,两者在不同的组合问题中有广泛的应用。本节将详细介绍斯特林数的定义、性质以及应用。
第二类斯特林数
虽然被称作「第二类」,第二类斯特林数却在斯特林的相关著作和具体数学中被首先描述,同时也比第一类斯特林数常用得多。
定义
第二类斯特林数(斯特林子集数) {nk}\begin{Bmatrix}n\\ k\end{Bmatrix}{nk},也可记作 S(n,k)S(n,k)S(n,k),表示将 nnn 个两两不同的元素,划分为 kkk 个互不区分的非空子集的方案数。
递推式
第二类斯特林数的递推公式为:

边界条件为:

组合意义证明
我们插入一个新元素时,有两种方案:
根据加法原理,将两式相加即可得到递推式。
通项公式
第二类斯特林数的通项公式为:

使用容斥原理证明该公式。设将 nnn 个两两不同的元素,划分到 iii 个两两不同的集合(允许空集)的方案数为 GiG_iGi,将 nnn 个两两不同的元素,划分到 iii 个两两不同的非空集合(不允许空集)的方案数为 FiF_iFi。
显然:

根据二项式反演:

考虑 FiF_iFi 与 {ni}\begin{Bmatrix}n\\i\end{Bmatrix}{ni} 的关系。第二类斯特林数要求集合之间互不区分,因此 FiF_iFi 正好就是 {ni}\begin{Bmatrix}n\\i\end{Bmatrix}{ni} 的 i!i!i! 倍。于是:

同一行第二类斯特林数的计算

根据上面给出的通项公式,卷积计算即可。该做法的时间复杂度为 O(nlogn)O(n \log n)O(nlogn)。
下面的代码使用了名为 poly 的多项式类,仅供参考。
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <vector>
namespace fstdlib {
typedef long long ll;
int mod = 998244353, grt = 3;
class poly {
private:
std::vector<int> data;
public:
poly(std::size_t len = std::size_t(0)) { data = std::vector<int>(len); }
poly(const std::vector<int> &b) { data = b; }
poly(const poly &b) { data = b.data; }
void resize(std::size_t len, int val = 0) { data.resize(len, val); }
std::size_t size(void) const { return data.size(); }
int &operator[](std::size_t b) { return data[b]; }
const int &operator[](std::size_t b) const { return data[b]; }
poly operator*(const poly &h) const;
poly operator*=(const poly &h);
poly operator*(const int &h) const;
poly operator*=(const int &h);
poly operator+(const poly &h) const;
poly operator+=(const poly &h);
poly operator-(const poly &h) const;
poly operator-=(const poly &h);
poly operator<<(const std::size_t &b) const;
poly operator<<=(const std::size_t &b);
poly operator>>(const std::size_t &b) const;
poly operator>>=(const std::size_t &b);
poly operator/(const int &h) const;
poly operator/=(const int &h);
poly inv(void) const;
};
int qpow(int a, int b, int p = mod) {
int res = 1;
while (b) {
if (b & 1) res = (ll)res * a % p;
a = (ll)a * a % p, b >>= 1;
}
return res;
}
std::vector<int> rev;
void dft_for_module(std::vector<int> &f, int n, int b) {
static std::vector<int> w;
w.resize(n);
for (int i = 0; i < n; ++i)
if (i < rev[i]) std::swap(f[i], f[rev[i]]);
for (int i = 2; i <= n; i <<= 1) {
w[0] = 1, w[1] = qpow(grt, (mod - 1) / i);
if (b == -1) w[1] = qpow(w[1], mod - 2);
for (int j = 2; j < i / 2; ++j) w[j] = (ll)w[j - 1] * w[1] % mod;
for (int j = 0; j < n; j += i)
for (int k = 0; k < i / 2; ++k) {
int p = f[j + k], q = (ll)f[j + k + i / 2] * w[k] % mod;
f[j + k] = (p + q) % mod, f[j + k + i / 2] = (p - q + mod) % mod;
}
}
}
poly poly::operator*(const poly &h) const {
int N = 1;
while (N < (int)(size() + h.size() - 1)) N <<= 1;
std::vector<int> f(this->data), g(h.data);
f.resize(N), g.resize(N);
rev.resize(N);
for (int i = 0; i < N; ++i)
rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? N >> 1 : 0);
dft_for_module(f, N, 1), dft_for_module(g, N, 1);
for (int i = 0; i < N; ++i) f[i] = (ll)f[i] * g[i] % mod;
dft_for_module(f, N, -1), f.resize(size() + h.size() - 1);
for (int i = 0, inv = qpow(N, mod - 2); i < (int)f.size(); ++i)
f[i] = (ll)f[i] * inv % mod;
return f;
}
poly poly::operator*=(const poly &h) { return *this = *this * h; }
poly poly::operator*(const int &h) const {
std::vector<int> f(this->data);
for (int i = 0; i < (int)f.size(); ++i) f[i] = (ll)f[i] * h % mod;
return f;
}
poly poly::operator*=(const int &h) {
for (int i = 0; i < (int)size(); ++i) data[i] = (ll)data[i] * h % mod;
return *this;
}
poly poly::operator+(const poly &h) const {
std::vector<int> f(this->data);
if (f.size() < h.size()) f.resize(h.size());
for (int i = 0; i < (int)h.size(); ++i) f[i] = (f[i] + h[i]) % mod;
return f;
}
poly poly::operator+=(const poly &h) {
std::vector<int> &f = this->data;
if (f.size() < h.size()) f.resize(h.size());
for (int i = 0; i < (int)h.size(); ++i) f[i] = (f[i] + h[i]) % mod;
return f;
}
poly poly::operator-(const poly &h) const {
std::vector<int> f(this->data);
if (f.size() < h.size()) f.resize(h.size());
for (int i = 0; i < (int)h.size(); ++i) f[i] = (f[i] - h[i] + mod) % mod;
return f;
}
poly poly::operator-=(const poly &h) {
std::vector<int> &f = this->data;
if (f.size() < h.size()) f.resize(h.size());
for (int i = 0; i < (int)h.size(); ++i) f[i] = (f[i] - h[i] + mod) % mod;
return f;
}
poly poly::operator<<(const std::size_t &b) const {
std::vector<int> f(size() + b);
for (int i = 0; i < (int)size(); ++i) f[i + b] = data[i];
return f;
}
poly poly::operator<<=(const std::size_t &b) { return *this = (*this) << b; }
poly poly::operator>>(const std::size_t &b) const {
std::vector<int> f(size() - b);
for (int i = 0; i < (int)f.size(); ++i) f[i] = data[i + b];
return f;
}
poly poly::operator>>=(const std::size_t &b) { return *this = (*this) >> b; }
poly poly::operator/(const int &h) const {
std::vector<int> f(this->data);
int inv = qpow(h, mod - 2);
for (int i = 0; i < (int)f.size(); ++i) f[i] = (ll)f[i] * inv % mod;
return f;
}
poly poly::operator/=(const int &h) {
int inv = qpow(h, mod - 2);
for (int i = 0; i < (int)data.size(); ++i) data[i] = (ll)data[i] * inv % mod;
return *this;
}
poly poly::inv(void) const {
int N = 1;
while (N < (int)(size() + size() - 1)) N <<= 1;
std::vector<int> f(N), g(N), d(this->data);
d.resize(N), f[0] = qpow(d[0], mod - 2);
for (int w = 2; w < N; w <<= 1) {
for (int i = 0; i < w; ++i) g[i] = d[i];
rev.resize(w << 1);
for (int i = 0; i < w * 2; ++i)
rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? w : 0);
dft_for_module(f, w << 1, 1), dft_for_module(g, w << 1, 1);
for (int i = 0; i < w * 2; ++i)
f[i] = (ll)f[i] * (2 + mod - (ll)f[i] * g[i] % mod) % mod;
dft_for_module(f, w << 1, -1);
for (int i = 0, inv = qpow(w << 1, mod - 2); i < w; ++i)
f[i] = (ll)f[i] * inv % mod;
for (int i = w; i < w * 2; ++i) f[i] = 0;
}
f.resize(size());
return f;
}
poly poly::operator==(const poly &h) const {
if (size() != h.size()) return 0;
for (int i = 0; i < (int)size(); ++i)
if (data[i] != h[i]) return 0;
return 1;
}
poly poly::operator!=(const poly &h) const {
if (size() != h.size()) return 1;
for (int i = 0; i < (int)size(); ++i)
if (data[i] != h[i]) return 1;
return 0;
}
poly poly::operator+(const int &h) const {
poly f(this->data);
f[0] = (f[0] + h) % mod;
return f;
}
poly poly::operator+=(const int &h) { return *this = (*this) + h; }
poly poly::inv(const int &h) const {
poly f(*this);
f.resize(h);
return f.inv();
}
} // namespace fstdlib
int main() {
int n;
scanf("%d", &n);
std::vector<int> fact(n + 1), ifact(n + 1);
fact[0] = 1;
for (int i = 1; i <= n; ++i) fact[i] = (ll)fact[i - 1] * i % mod;
ifact[n] = fstdlib::qpow(fact[n], mod - 2);
for (int i = n - 1; i >= 0; --i) ifact[i] = (ll)ifact[i + 1] * (i + 1) % mod;
fstdlib::poly f(n + 1), g(n + 1);
for (int i = 0; i <= n; ++i)
g[i] = (i & 1 ? mod - 1ll : 1ll) * ifact[i] % mod,
f[i] = (ll)fstdlib::qpow(i, n) * ifact[i] % mod;
f *= g, f.resize(n + 1);
for (int i = 0; i <= n; ++i) printf("%d ", f[i]);
return 0;
}
同一列第二类斯特林数的计算
「同一列」的第二类斯特林数指的是,有着不同的 iii,相同的 kkk 的一系列 {ik}\begin{Bmatrix}i\\k\end{Bmatrix}{ik}。求出同一列的所有第二类斯特林数,就是对 i=0..ni=0..ni=0..n 求出了将 iii 个不同元素划分为 kkk 个非空集的方案数。
利用指数型生成函数计算。
一个盒子装 iii 个物品且盒子非空的方案数是 [i>0][i>0][i>0]。我们可以写出它的指数型生成函数为:

经过之前的学习,我们明白 Fk(x)F^k(x)Fk(x) 就是 iii 个有标号物品放到 kkk 个有标号盒子里的指数型生成函数,那么除掉 k!k!k! 就是 iii 个有标号物品放到 kkk 个无标号盒子里的指数型生成函数。

O(nlogn)O(n\log n)O(nlogn) 计算多项式幂即可。
另外:

就是 iii 个有标号物品放到任意多个无标号盒子里的指数型生成函数(EXP 通过每项除以一个 i!i!i! 去掉了盒子的标号)。这其实就是贝尔数的生成函数。
下面是计算第二类斯特林数的实现代码:
int main() {
int n, k;
scanf("%d%d", &n, &k);
std::vector<int> fact(n + 1);
fact[0] = 1;
for (int i = 1; i <= n; ++i) fact[i] = (ll)fact[i - 1] * i % mod;
fstdlib::poly f(n + 1);
for (int i = 1; i <= n; ++i) f[i] = fstdlib::qpow(fact[i], mod - 2);
f = fstdlib::exp(fstdlib::log(f >> 1) * k) << k;
f.resize(n + 1);
int inv = fstdlib::qpow(fact[k], mod - 2);
for (int i = 0; i <= n; ++i)
printf("%lld ", (ll)f[i] * fact[i] % mod * inv % mod);
return 0;
}
第一类斯特林数
定义

递推式
第一类斯特林数的递推公式为:

边界条件为:

组合意义证明
我们插入一个新元素时,有两种方案:
根据加法原理,将两式相加即可得到递推式。
通项公式
第一类斯特林数没有实用的通项公式。
同一行第一类斯特林数的计算
类似第二类斯特林数,我们构造同行第一类斯特林数的生成函数,即:
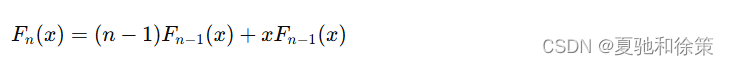
根据递推公式,不难写出:
Fn(x)=(n−1)Fn−1(x)+xFn−1(x)F_n(x)=(n-1)F_{n-1}(x)+xF_{n-1}(x)Fn(x)=(n−1)Fn−1(x)+xFn−1(x)
于是:

这其实是 xxx 的 nnn 次上升阶乘幂,记做 xn‾x^{\overline n}xn。这个东西自然是可以暴力分治乘 O(nlog2n)O(n\log^2n)O(nlog2n) 求出的,但用上升幂相关做法可以 O(nlogn)O(n\log n)O(nlogn) 求出。
下面是计算第一类斯特林数的实现代码:
int main() {
int n, k;
scanf("%d%d", &n, &k);
std::vector<int> fact(n + 1), ifact(n + 1);
fact[0] = 1;
for (int i = 1; i <= n; ++i) fact[i] = (ll)fact[i - 1] * i % mod;
ifact[n] = fstdlib::qpow(fact[n], mod - 2);
for (int i = n - 1; i >= 0; --i) ifact[i] = (ll)ifact[i + 1] * (i + 1) % mod;
fstdlib::poly f(n + 1);
for (int i = 1; i <= n; ++i) f[i] = (ll)fact[i - 1] * ifact[i] % mod;
f = fstdlib::exp(fstdlib::log(f >> 1) * k) << k;
f.resize(n + 1);
for (int i = 0; i <= n; ++i)
printf("%lld ", (ll)f[i] * fact[i] % mod * ifact[k] % mod);
return 0;
}
应用
上升幂与普通幂的相互转化
上升阶乘幂 xn‾x^{\overline{n}}xn 可以表示为:

则可以利用下面的恒等式将上升幂转化为普通幂:

如果将普通幂转化为上升幂,则有下面的恒等式:

下降幂与普通幂的相互转化
下降阶乘幂 xn‾x^{\underline{n}}xn 可以表示为:

则可以利用下面的恒等式将普通幂转化为下降幂:

如果将下降幂转化为普通幂,则有下面的恒等式:

多项式下降阶乘幂表示与多项式点值表示的关系
在这里,多项式的下降阶乘幂表示就是用:

的形式表示一个多项式,而点值表示就是用 n+1n+1n+1 个点 (i,ai),i=0..n(i,a_i), i=0..n(i,ai),i=0..n 来表示一个多项式。
显然,下降阶乘幂 bbb 和点值 aaa 间满足这样的关系:

即:

这是一个卷积形式的式子,我们可以在 O(nlogn)O(n\log n)O(nlogn) 的时间复杂度内完成点值和下降阶乘幂的互相转化。
习题
- HDU3625 Examining the Rooms
- UOJ540 联合省选 2020 组合数问题
- UOJ269 清华集训 2016 如何优雅地求和









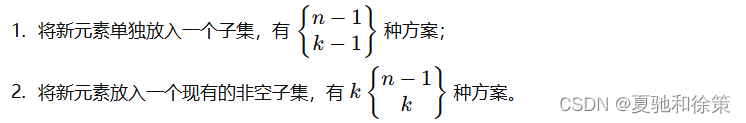

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










