8.14.13 ACM-ICPC 组合数学：分拆数
一、分拆数的定义
在组合数学中，分拆数（Partition Number）是指将一个正整数 nnn 分拆为若干个正整数之和的不同方式的总数。例如，整数 444 的分拆可以表示为：
因此，整数 444 的分拆数是 5。
分拆数 p(n)p(n)p(n) 是表示 nnn 的不同分拆方式的总数。分拆数在组合数学中具有重要意义，并且与生成函数、递归关系和对称性等概念密切相关。
二、分拆数的生成函数
生成函数是解决组合数学问题的一种有力工具。分拆数的生成函数 P(x)P(x)P(x) 定义如下：
分拆数生成函数可以表示为无限乘积形式：
这个公式的推导基于每个正整数 kkk 的选择是否包含在分拆中的独立性。每个因子 11−xk\frac{1}{1 - x^k}1−xk1 表示整数 kkk 可以在分拆中出现任意次。
三、分拆数的递归关系
分拆数可以通过递归关系来计算。对于整数 nnn，分拆数 p(n)p(n)p(n) 满足以下递归关系：
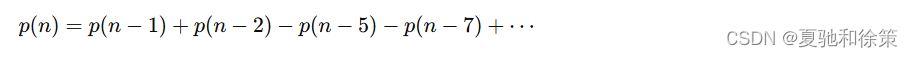
这个递归关系由德国数学家莱昂哈德·欧拉（Leonhard Euler）提出，称为欧拉的五边形数定理。递归关系中的每一项都涉及到一个五边形数，这些数的符号交替，系数根据五边形数的索引来确定。
四、分拆数的计算方法
分拆数的计算方法包括递归法和动态规划法。递归法利用上述递归关系直接计算，而动态规划法则通过建立一个表格，从小到大逐步计算分拆数。
动态规划法示例
假设我们需要计算 p(10)p(10)p(10)，可以使用以下动态规划算法：
def partition_number(n):
partitions = [1] + [0] * n
for i in range(1, n+1):
for j in range(i, n+1):
partitions[j] += partitions[j - i]
return partitions[n]
print(partition_number(10)) # 输出：42
在这个算法中，我们首先初始化一个长度为 n+1n+1n+1 的数组 partitions，其中 partitions[0] = 1，表示 p(0)=1p(0) = 1p(0)=1。然后，我们通过两个嵌套的循环来更新每个 partitions[j] 的值，最终得到 p(n)p(n)p(n) 的值。
五、分拆数的应用
分拆数在许多数学领域和实际应用中都有重要作用。例如：
- 数论：分拆数在研究整数性质和素数分布中起到重要作用。
- 组合设计：在设计组合算法和组合结构时，分拆数提供了基本工具。
- 物理学：在统计力学和量子力学中，分拆数用于描述系统的状态数。
- 计算机科学：在算法设计和分析中，分拆数用于解决优化和计数问题。
六、经典例题
例题1：计算小整数的分拆数
求整数 5 的分拆数。
解：
根据定义，整数 555 的分拆包括：
因此，整数 555 的分拆数是 7。
例题2：利用动态规划计算分拆数
使用动态规划算法计算整数 888 的分拆数。
解：
print(partition_number(8)) # 输出：22
通过上述动态规划算法可以得到整数 888 的分拆数是 22。
七、总结
分拆数是组合数学中的重要概念，涉及到生成函数、递归关系和动态规划等多种方法。分拆数不仅在理论数学中具有重要地位，而且在实际应用中也发挥着重要作用。理解和掌握分拆数的计算方法和性质，对于深入研究组合数学和解决实际问题具有重要意义。
分拆数
分拆是将自然数 nnn 写成递降正整数和的表示。 
其中每个正整数称为一个部分。
分拆数 pnp_npn 是自然数 nnn 的分拆方法数。
自 0 开始的分拆数：
| nnn | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| pnp_npn | 1 | 1 | 2 | 3 | 5 | 7 | 11 | 15 | 22 |
kkk 部分拆数
将 nnn 分成恰有 kkk 个部分的分拆，称为 kkk 部分拆数，记作 p(n,k)p(n,k)p(n,k)。
显然，kkk 部分拆数 p(n,k)p(n,k)p(n,k) 同时也是下面方程的解数： 
如果这个方程里恰有 jjj 个部分非 0，则恰有 p(n−k,j)p(n-k,j)p(n−k,j) 个解。因此有和式：
相邻两个和式作差，得：
表格展示：
| kkk | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| p(0,k)p(0,k)p(0,k) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| p(1,k)p(1,k)p(1,k) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| p(2,k)p(2,k)p(2,k) | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| p(3,k)p(3,k)p(3,k) | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| p(4,k)p(4,k)p(4,k) | 0 | 1 | 2 | 1 | 1 | 0 | 0 | 0 | 0 |
| p(5,k)p(5,k)p(5,k) | 0 | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0 |
| p(6,k)p(6,k)p(6,k) | 0 | 1 | 3 | 3 | 2 | 1 | 1 | 0 | 0 |
| p(7,k)p(7,k)p(7,k) | 0 | 1 | 3 | 4 | 3 | 2 | 1 | 1 | 0 |
| p(8,k)p(8,k)p(8,k) | 0 | 1 | 4 | 5 | 5 | 3 | 2 | 1 | 1 |
例题：计算 kkk 部分拆数
计算 kkk 部分拆数 p(n,k)p(n,k)p(n,k)。多组输入，其中 nnn 上界为 10000，kkk 上界为 1000，对 1000007 取模。
程序：
#include <stdio.h>
#include <string.h>
int p[10005][1005]; /*将自然数n分拆为k个部分的方法数*/
int main() {
int n, k;
while (~scanf("%d%d", &n, &k)) {
memset(p, 0, sizeof(p));
p[0][0] = 1;
int i;
for (i = 1; i <= n; ++i) {
int j;
for (j = 1; j <= k; ++j) {
if (i - j >= 0) {
p[i][j] = (p[i - j][j] + p[i - 1][j - 1]) % 1000007;
}
}
}
printf("%d\n", p[n][k]);
}
}
生成函数
由等比数列求和公式，有：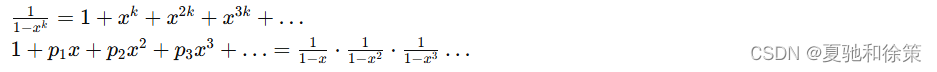 
对于 kkk 部分拆数，生成函数稍微复杂。具体写出如下： 
Ferrers 图
Ferrers 图：将分拆的每个部分用点组成的行表示。每行点的个数为这个部分的大小。根据分拆的定义，Ferrers 图中不同的行按照递减的次序排放，最长行在最上面。例如：分拆 12=5+4+2+112 = 5 + 4 + 2 + 112=5+4+2+1 的 Ferrers 图。
将一个 Ferrers 图沿着对角线翻转，得到的新 Ferrers 图称为原图的共轭，新分拆称为原分拆的共轭。例如，分拆 12=5+4+2+112 = 5 + 4 + 2 + 112=5+4+2+1 的共轭是分拆 12=4+3+2+2+112 = 4 + 3 + 2 + 2 + 112=4+3+2+2+1。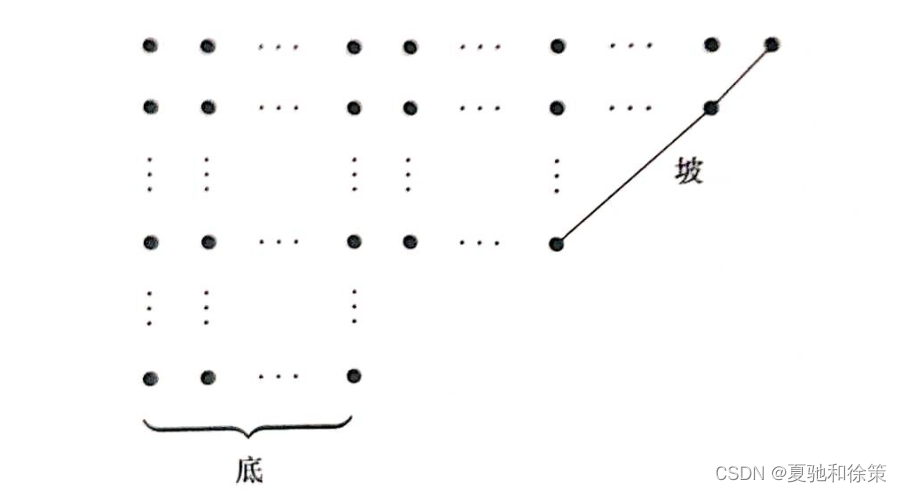
互异分拆数
互异分拆数 pdnpd_npdn 是自然数 nnn 的各部分互不相同的分拆方法数。
自 0 开始的互异分拆数：
| nnn | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| pdnpd_npdn | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 5 | 6 |
同样地，定义互异 kkk 部分拆数 pd(n,k)pd(n,k)pd(n,k)，表示最大拆出 kkk 个部分的互异分拆。递推式为：
表格展示：
| kkk | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| pd(0,k)pd(0,k)pd(0,k) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| pd(1,k)pd(1,k)pd(1,k) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| pd(2,k)pd(2,k)pd(2,k) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| pd(3,k)pd(3,k)pd(3,k) | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| pd(4,k)pd(4,k)pd(4,k) | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| pd(5,k)pd(5,k)pd(5,k) | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| pd(6,k)pd(6,k)pd(6,k) | 0 | 1 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
| pd(7,k)pd(7,k)pd(7,k) | 0 | 1 | 3 | 1 | 0 | 0 | 0 | 0 | 0 |
| pd(8,k)pd(8,k)pd(8,k) | 0 | 1 | 3 | 2 | 0 | 0 | 0 | 0 | 0 |
例题：计算互异分拆数
计算互异分拆数 pdnpd_npdn。多组输入，其中 nnn 上界为 50000，对 1000007 取模。
程序：
#include <stdio.h>
#include <string.h>
int pd[50005][2]; /*将自然数n分拆为k个部分的互异方法数*/
int main() {
int n;
while (~scanf("%d", &n)) {
memset(pd, 0, sizeof(pd));
pd[0][0] = 1;
int ans = 0;
int j;
for (j = 1; j < 350; ++j) {
int i;
for (i = 0; i < 350; ++i) {
pd[i][j & 1] = 0;
}
for (i = 0; i <= n; ++i) {
if (i - j >= 0) {
pd[i][j & 1] = (pd[i - j][j & 1] + pd[i - j][(j - 1) & 1]) % 1000007;
}
}
ans = (ans + pd[n][j & 1]) % 1000007;
}
printf("%d\n", ans);
}
}
奇分拆数
奇分拆数 ponpo_npon 是自然数 nnn 的各部分都是奇数的分拆方法数。显然，奇分拆数和互异分拆数相同：
五边形数定理
观察分拆数的生成函数的分母部分： 
将这部分展开，可以得到分拆数的生成函数。对于任意自然数 nnn，有：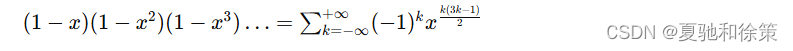 
递推式：
例题：计算分拆数
计算分拆数 pnp_npn。多组输入，其中 nnn 上界为 50000，对 1000007 取模。
程序：
#include <stdio.h>
long long a[100010];
long long p[50005];
int main() {
p[0] = 1;
p[1] = 1;
p[2] = 2;
int i;
for (i = 1; i < 50005; i++) {
a[2 * i] = i * (i * 3 - 1) / 2;
a[2 * i + 1] = i * (i * 3 + 1) / 2;
}
for (i = 3; i < 50005; i++) {
p[i] = 0;
int j;
for (j = 2; a[j] <= i; j++) {
if (j & 2) {
p[i] = (p[i] + p[i - a[j]] + 1000007) % 1000007;
} else {
p[i] = (p[i] - p[i - a[j]] + 1000007) % 1000007;
}
}
}
int n;
while (~scanf("%d", &n)) {
printf("%lld\n", p[n]);
}
}
以上便是对分拆数、互异分拆数、奇分拆数及五边形数定理的介绍与应用示例。希望这些内容能够帮助你更好地理解组合数学中的分拆数问题。
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
