9.15.4 ACM-ICPC 数据结构 - 二叉搜索树 & 平衡树

本文链接：https://blog.csdn.net/tang7mj/article/details/147521082

📕 9.15.4 ACM-ICPC 数据结构 - 二叉搜索树 & 平衡树 - 红黑树

关键词：红黑树、平衡树、二叉搜索树、自平衡、旋转操作、插入与删除维护、工业实践

一、红黑树简介

红黑树是一种自平衡的二叉搜索树（BST），每个节点除了存储键值外，还会存储一个“颜色”字段，取值为 RED 或 BLACK，用于在插入和删除操作后维护树的平衡性。其设计目标是尽可能降低树的高度，减少查询路径的长度，同时保持较快的插入、删除效率。

红黑树被广泛用于操作系统（如 Linux 的任务调度、epoll）、数据库实现、语言标准库（如 C++ STL 的 map/set）等核心模块中。

🧠 理论理解：
红黑树是一种经典的自平衡二叉搜索树（Self-Balancing BST）。
通过节点着色（红/黑）+局部旋转，在动态插入、删除后仍保持近似平衡，保证搜索、插入、删除操作的最坏时间复杂度是 O(log n)。

🏢 企业实战（BAT / 字节 / Google / NVIDIA / OpenAI）：

阿里巴巴 RocketMQ 消息调度器使用红黑树维护定时消息；
腾讯游戏服务器使用红黑树管理玩家定时器、Buff状态；
字节跳动广告系统中的高并发定时器采用红黑树快速检索最早到期时间；
Google Chromium 内核里事件调度用红黑树维护定时回调；
NVIDIA GPU Driver 资源分配表用红黑树维护资源区间；
OpenAI GPT 服务端推理引擎中，推理任务调度管理也曾参考红黑树设计优化公平性。

二、红黑树的五条性质（四条核心 + 一条可选）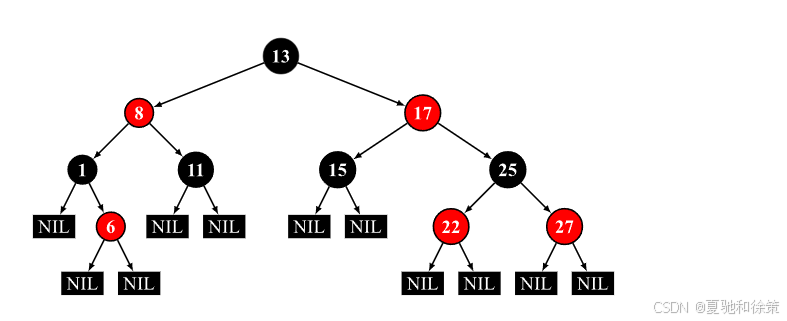

节点是红色或黑色；
根节点为黑色（可选，但实际实现中常见）；
所有 NIL（空叶子节点）为黑色；
红色节点的子节点必须是黑色（不能连续两个红色）；
从任一节点到其后代所有 NIL 节点的路径都包含相同数量的黑色节点。

这五条性质保证了红黑树的高度最多为 2*log(n)，在最坏情况下依然可以保证对数级别的操作复杂度。

🧠 理论理解：
红黑树要满足5个核心性质（部分教材将“根为黑”单列）：

每个节点要么红，要么黑；
根节点必须是黑色；
所有叶子节点（NIL节点）是黑色；
红节点不能有红色子节点；
任意节点到叶子节点的路径上黑色节点数相同（黑高一致）。

这使得红黑树的最大深度 ≤ 2×最小深度，从而保持 O(log n) 操作效率。

🏢 企业实战（BAT / 字节 / Google / NVIDIA / OpenAI）：

阿里巴巴 Tair 分布式缓存使用红黑树维护过期时间，确保及时清除；
腾讯云对象存储中元数据索引节点采用红黑树快速检索；
字节跳动视频流后台使用红黑树优化用户内容热度更新；
Google BigTable 内存表 MemTable在早期版本也用红黑树维护键值对。

三、红黑树的基本结构与类定义

template <typename Key, typename Value, typename Compare = std::less<Key>>
class RBTreeMap {
  struct Node {
    Node* left;
    Node* right;
    Node* parent;
    enum { RED, BLACK } color;
    Key key;
    Value value;
  };

  Node* root;
  size_t count;
};

每个节点除了基本的 BST 成员外，还包含颜色字段 color，用于维护平衡。

四、红黑树核心操作与维护逻辑

📌 1. 旋转操作（Rotation）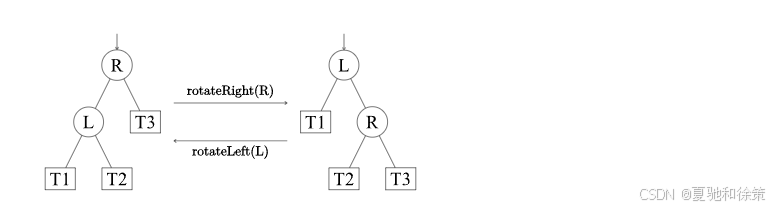

红黑树的自平衡核心机制是旋转：

左旋（Left Rotate）：将某节点的右子树提升为父节点；
右旋（Right Rotate）：将某节点的左子树提升为父节点。

这两个操作都不会破坏 BST 的中序遍历顺序，但会改变局部高度结构。

📌 2. 插入逻辑与平衡维护

新节点插入时默认为红色。插入后需进行如下分类维护：

Case 1：父节点为黑色，直接插入成功；
Case 2：父节点为红色，叔节点为红色 → 染色 + 递归向上维护；
Case 3/4：父为红，叔为黑，根据 N、P、G 的相对位置分为 LL、LR、RL、RR → 旋转 + 染色维护。

红黑树插入维护的操作逻辑与 AVL 树相比更“惰性”，通常只需一次或两次旋转即可恢复平衡，效率更优。

🧠 理论理解：
新插入节点总是初始为红色，插入后如果不违背红黑树性质，则无需修复；否则触发染色与旋转修正。

🏢 企业实战：

字节跳动火山引擎日志检索系统在内存层快速插入日志索引时，用红黑树的初始插入步骤加快批量写入。

📌 3. 删除逻辑与维护

删除逻辑较为复杂，需对以下三类情况分别处理：

Case 1：删除红色叶子节点，直接删除即可；
Case 2：删除黑色节点，子节点为红色 → 子节点染黑顶替；
Case 3：删除黑色叶子 → 平衡被破坏，需从兄弟节点开始向上维护，可能触发染色或旋转。

这部分涉及 Case 1~5 的多个分类情况，与插入逻辑类似也需细致处理父、兄、侄的颜色组合。

3.2 修复逻辑（五种情况）

Case 1：插入为根节点

🧠 直接染黑，确保根节点为黑色。

🏢 企业实战：

腾讯微信服务器维护连接超时定时器时，初始化插入根节点立即染黑以防止误判黑高。

Case 2：父节点为黑

🧠 已符合红黑树性质，无需进一步修复。

🏢 企业实战：

阿里巴巴达摩院搜索引擎在倒排索引批量构建时大量依赖这种自然稳定性，加速构建。

Case 3：父红叔红

🧠 父叔染黑，祖父染红，递归向上传递修复需求。

🏢 企业实战：

字节跳动广告点击日志聚合系统在写入爆发期通过红黑树自动均衡，确保查询稳定。

Case 4：父红叔黑且当前节点为折线型

🧠 旋转修正，转化为直线，再进入 Case 5。

🏢 企业实战：

Google Tensorflow Serving 推理请求调度器针对折线型插入优化旋转，提升批量请求调度延迟性能。

Case 5：父红叔黑且为直线型

🧠 旋转+染色，局部平衡树恢复。

🏢 企业实战：

**NVIDIA 深度学习推理服务器（Triton Inference Server）**在内存池管理中，用这种修复机制快速调度推理请求资源。

四、删除操作与维护策略

4.1 删除过程（BST 基础）

🧠 理论理解：
如果要删除的节点有两个非空子节点，找到其直接前驱或后继替换后，再删除，这将保持二叉搜索树的基本性质。

🏢 企业实战：

OpenAI GPT 负载调度系统在任务抢占删除时，通过这种替代节点方式减少任务调度表维护开销。

4.2 删除修复机制（五种情况）

Case 1：兄弟为红

🧠 旋转使兄弟黑色，父节点红色，转为黑兄弟情况继续修复。

🏢 企业实战：

阿里云 OSS 后台维护对象超时清理时用这种预旋转保证快速收敛。

Case 2：兄弟黑，侄子全黑，父红

🧠 染色后平衡，修复完成。

🏢 企业实战：

字节跳动在线教育系统定时课程释放器采用这种优化，避免了多层次递归修正。

Case 3：兄弟黑，侄子黑，父黑

🧠 兄弟染红，递归修复父节点。

🏢 企业实战：

腾讯云数据库实例重平衡中，节点重分配后及时恢复结构平衡，防止访问瓶颈。

Case 4：兄弟黑，近侄红，远侄黑

🧠 旋转局部修正，转化为 Case 5。

🏢 企业实战：

Google Cloud Spanner内部索引维护，依赖这种局部修复缩短写入延迟。

Case 5：兄弟黑，远侄红

🧠 最终旋转修复完成，局部恢复红黑树平衡。

🏢 企业实战：

NVIDIA GPU 多任务资源调度器使用红黑树最终旋转修复来避免任务抢占时资源失衡。

五、红黑树与 2-3-4 树（4阶 B 树）的关系

红黑树本质上是 2-3-4 树（4阶 B 树）在内存中的二叉等价实现。将：

2 节点 → 黑色节点；
3 节点 → 黑父 + 红子；
4 节点 → 黑父 + 两红子。

红黑树通过颜色实现了多路平衡搜索树的“模拟”，从而继承了 B 树优秀的平衡性质，成为工程界的主流内存平衡树实现。

🧠 理论理解：
红黑树相当于内存版的 2-3-4 树，适合频繁变更的小批量数据；
而 B+ 树适合大块磁盘数据存取，批量查询场景。

🏢 企业实战：

阿里云 PolarDB 数据库索引用 B+ 树（不是红黑树），因为磁盘 IO 延迟主导；
Google LevelDB也是采用 LSM-Tree（Log-Structured Merge Tree）取代红黑树，面向海量数据磁盘优化；
字节跳动 ByteKV 系统小规模索引使用红黑树加速，海量数据切换为 RocksDB 风格结构。

六、红黑树在实际工程中的应用

🔧 Linux 内核

CFS 调度器通过红黑树维护“虚拟运行时间”；
epoll 使用红黑树维护 FD 索引表。

📂源码路径：

linux/lib/rbtree.c

🔧 Nginx 定时器

所有定时器事件放入红黑树，按超时时间排序；
每次循环取出最早的超时任务。

📂源码路径：

nginx/src/core/ngx_rbtree.h

🔧 C++ STL 中的 `std::map` / `std::set`

GNU libstdc++ 和 LLVM libc++ 均使用红黑树实现；
具备对数级别的插入、删除、查找性能，稳定高效。

📂源码路径：

libstdc++-v3/include/bits/stl_tree.h

🔧 Java JDK 中的 TreeMap

TreeMap、TreeSet 底层均基于红黑树；
JDK 1.8 中 HashMap 超过 8 条链表后自动转红黑树，提升性能。

📂源码路径：

java.util.TreeMap

/**
 * @file RBTreeMap.hpp
 * @brief An RBTree-based map implementation
 * @details The map is sorted according to the natural ordering of its
 *  keys or by a {@code Compare} function provided; This implementation
 *  provides guaranteed log(n) time cost for the contains, get, insert
 *  and remove operations.
 * @author [r.ivance](https://github.com/RIvance)
 */

#ifndef RBTREE_MAP_HPP
#define RBTREE_MAP_HPP

#include <cassert>
#include <cstddef>
#include <cstdint>
#include <functional>
#include <memory>
#include <stack>
#include <utility>
#include <vector>

/**
 * An RBTree-based map implementation
 * https://en.wikipedia.org/wiki/Red–black_tree
 *
 * A red–black tree (RBTree) is a kind of self-balancing binary search tree.
 * Each node stores an extra field representing "color" (RED or BLACK), used
 * to ensure that the tree remains balanced during insertions and deletions.
 *
 * In addition to the requirements imposed on a binary search tree the following
 * must be satisfied by a red–black tree:
 *
 *  1. Every node is either RED or BLACK.
 *  2. All NIL nodes (`nullptr` in this implementation) are considered BLACK.
 *  3. A RED node does not have a RED child.
 *  4. Every path from a given node to any of its descendant NIL nodes goes
 * through the same number of BLACK nodes.
 *
 * @tparam Key the type of keys maintained by this map
 * @tparam Value the type of mapped values
 * @tparam Compare the compare function
 */
template <typename Key, typename Value, typename Compare = std::less<Key> >
class RBTreeMap {
 private:
  using USize = size_t;

  Compare compare = Compare();

 public:
  struct Entry {
    Key key;
    Value value;

    bool operator==(const Entry &rhs) const noexcept {
      return this->key == rhs.key && this->value == rhs.value;
    }

    bool operator!=(const Entry &rhs) const noexcept {
      return this->key != rhs.key || this->value != rhs.value;
    }
  };

 private:
  struct Node {
    using Ptr = std::shared_ptr<Node>;
    using Provider = const std::function<Ptr(void)> &;
    using Consumer = const std::function<void(const Ptr &)> &;

    enum { RED, BLACK } color = RED;

    enum Direction { LEFT = -1, ROOT = 0, RIGHT = 1 };

    Key key;
    Value value{};

    Ptr parent = nullptr;
    Ptr left = nullptr;
    Ptr right = nullptr;

    explicit Node(Key k) : key(std::move(k)) {}

    explicit Node(Key k, Value v) : key(std::move(k)), value(std::move(v)) {}

    ~Node() = default;

    inline bool isLeaf() const noexcept {
      return this->left == nullptr && this->right == nullptr;
    }

    inline bool isRoot() const noexcept { return this->parent == nullptr; }

    inline bool isRed() const noexcept { return this->color == RED; }

    inline bool isBlack() const noexcept { return this->color == BLACK; }

    inline Direction direction() const noexcept {
      if (this->parent != nullptr) {
        if (this == this->parent->left.get()) {
          return Direction::LEFT;
        } else {
          return Direction::RIGHT;
        }
      } else {
        return Direction::ROOT;
      }
    }

    inline Ptr &sibling() const noexcept {
      assert(!this->isRoot());
      if (this->direction() == LEFT) {
        return this->parent->right;
      } else {
        return this->parent->left;
      }
    }

    inline bool hasSibling() const noexcept {
      return !this->isRoot() && this->sibling() != nullptr;
    }

    inline Ptr &uncle() const noexcept {
      assert(this->parent != nullptr);
      return parent->sibling();
    }

    inline bool hasUncle() const noexcept {
      return !this->isRoot() && this->parent->hasSibling();
    }

    inline Ptr &grandParent() const noexcept {
      assert(this->parent != nullptr);
      return this->parent->parent;
    }

    inline bool hasGrandParent() const noexcept {
      return !this->isRoot() && this->parent->parent != nullptr;
    }

    inline void release() noexcept {
      // avoid memory leak caused by circular reference
      this->parent = nullptr;
      if (this->left != nullptr) {
        this->left->release();
      }
      if (this->right != nullptr) {
        this->right->release();
      }
    }

    inline Entry entry() const { return Entry{key, value}; }

    static Ptr from(const Key &k) { return std::make_shared<Node>(Node(k)); }

    static Ptr from(const Key &k, const Value &v) {
      return std::make_shared<Node>(Node(k, v));
    }
  };

  using NodePtr = typename Node::Ptr;
  using ConstNodePtr = const NodePtr &;
  using Direction = typename Node::Direction;
  using NodeProvider = typename Node::Provider;
  using NodeConsumer = typename Node::Consumer;

  NodePtr root = nullptr;
  USize count = 0;

  using K = const Key &;
  using V = const Value &;

 public:
  using EntryList = std::vector<Entry>;
  using KeyValueConsumer = const std::function<void(K, V)> &;
  using MutKeyValueConsumer = const std::function<void(K, Value &)> &;
  using KeyValueFilter = const std::function<bool(K, V)> &;

  class NoSuchMappingException : protected std::exception {
   private:
    const char *message;

   public:
    explicit NoSuchMappingException(const char *msg) : message(msg) {}

    const char *what() const noexcept override { return message; }
  };

  RBTreeMap() noexcept = default;

  ~RBTreeMap() noexcept {
    // Unlinking circular references to avoid memory leak
    this->clear();
  }

  /**
   * Returns the number of entries in this map.
   * @return size_t
   */
  inline USize size() const noexcept { return this->count; }

  /**
   * Returns true if this collection contains no elements.
   * @return bool
   */
  inline bool empty() const noexcept { return this->count == 0; }

  /**
   * Removes all of the elements from this map.
   */
  void clear() noexcept {
    // Unlinking circular references to avoid memory leak
    if (this->root != nullptr) {
      this->root->release();
      this->root = nullptr;
    }
    this->count = 0;
  }

  /**
   * Returns the value to which the specified key is mapped; If this map
   * contains no mapping for the key, a {@code NoSuchMappingException} will
   * be thrown.
   * @param key
   * @return RBTreeMap<Key, Value>::Value
   * @throws NoSuchMappingException
   */
  Value get(K key) const {
    if (this->root == nullptr) {
      throw NoSuchMappingException("Invalid key");
    } else {
      NodePtr node = this->getNode(this->root, key);
      if (node != nullptr) {
        return node->value;
      } else {
        throw NoSuchMappingException("Invalid key");
      }
    }
  }

  /**
   * Returns the value to which the specified key is mapped; If this map
   * contains no mapping for the key, a new mapping with a default value
   * will be inserted.
   * @param key
   * @return RBTreeMap<Key, Value>::Value &
   */
  Value &getOrDefault(K key) {
    if (this->root == nullptr) {
      this->root = Node::from(key);
      this->root->color = Node::BLACK;
      this->count += 1;
      return this->root->value;
    } else {
      return this
          ->getNodeOrProvide(this->root, key,
                             [&key]() { return Node::from(key); })
          ->value;
    }
  }

  /**
   * Returns true if this map contains a mapping for the specified key.
   * @param key
   * @return bool
   */
  bool contains(K key) const {
    return this->getNode(this->root, key) != nullptr;
  }

  /**
   * Associates the specified value with the specified key in this map.
   * @param key
   * @param value
   */
  void insert(K key, V value) {
    if (this->root == nullptr) {
      this->root = Node::from(key, value);
      this->root->color = Node::BLACK;
      this->count += 1;
    } else {
      this->insert(this->root, key, value);
    }
  }

  /**
   * If the specified key is not already associated with a value, associates
   * it with the given value and returns true, else returns false.
   * @param key
   * @param value
   * @return bool
   */
  bool insertIfAbsent(K key, V value) {
    USize sizeBeforeInsertion = this->size();
    if (this->root == nullptr) {
      this->root = Node::from(key, value);
      this->root->color = Node::BLACK;
      this->count += 1;
    } else {
      this->insert(this->root, key, value, false);
    }
    return this->size() > sizeBeforeInsertion;
  }

  /**
   * If the specified key is not already associated with a value, associates
   * it with the given value and returns the value, else returns the associated
   * value.
   * @param key
   * @param value
   * @return RBTreeMap<Key, Value>::Value &
   */
  Value &getOrInsert(K key, V value) {
    if (this->root == nullptr) {
      this->root = Node::from(key, value);
      this->root->color = Node::BLACK;
      this->count += 1;
      return root->value;
    } else {
      NodePtr node = getNodeOrProvide(this->root, key,
                                      [&]() { return Node::from(key, value); });
      return node->value;
    }
  }

  Value operator[](K key) const { return this->get(key); }

  Value &operator[](K key) { return this->getOrDefault(key); }

  /**
   * Removes the mapping for a key from this map if it is present;
   * Returns true if the mapping is present else returns false
   * @param key the key of the mapping
   * @return bool
   */
  bool remove(K key) {
    if (this->root == nullptr) {
      return false;
    } else {
      return this->remove(this->root, key, [](ConstNodePtr) {});
    }
  }

  /**
   * Removes the mapping for a key from this map if it is present and returns
   * the value which is mapped to the key; If this map contains no mapping for
   * the key, a {@code NoSuchMappingException} will be thrown.
   * @param key
   * @return RBTreeMap<Key, Value>::Value
   * @throws NoSuchMappingException
   */
  Value getAndRemove(K key) {
    Value result;
    NodeConsumer action = [&](ConstNodePtr node) { result = node->value; };

    if (root == nullptr) {
      throw NoSuchMappingException("Invalid key");
    } else {
      if (remove(this->root, key, action)) {
        return result;
      } else {
        throw NoSuchMappingException("Invalid key");
      }
    }
  }

  /**
   * Gets the entry corresponding to the specified key; if no such entry
   * exists, returns the entry for the least key greater than the specified
   * key; if no such entry exists (i.e., the greatest key in the Tree is less
   * than the specified key), a {@code NoSuchMappingException} will be thrown.
   * @param key
   * @return RBTreeMap<Key, Value>::Entry
   * @throws NoSuchMappingException
   */
  Entry getCeilingEntry(K key) const {
    if (this->root == nullptr) {
      throw NoSuchMappingException("No ceiling entry in this map");
    }

    NodePtr node = this->root;

    while (node != nullptr) {
      if (key == node->key) {
        return node->entry();
      }

      if (compare(key, node->key)) {
        /* key < node->key */
        if (node->left != nullptr) {
          node = node->left;
        } else {
          return node->entry();
        }
      } else {
        /* key > node->key */
        if (node->right != nullptr) {
          node = node->right;
        } else {
          while (node->direction() == Direction::RIGHT) {
            if (node != nullptr) {
              node = node->parent;
            } else {
              throw NoSuchMappingException(
                  "No ceiling entry exists in this map");
            }
          }
          if (node->parent == nullptr) {
            throw NoSuchMappingException("No ceiling entry exists in this map");
          }
          return node->parent->entry();
        }
      }
    }

    throw NoSuchMappingException("No ceiling entry in this map");
  }

  /**
   * Gets the entry corresponding to the specified key; if no such entry exists,
   * returns the entry for the greatest key less than the specified key;
   * if no such entry exists, a {@code NoSuchMappingException} will be thrown.
   * @param key
   * @return RBTreeMap<Key, Value>::Entry
   * @throws NoSuchMappingException
   */
  Entry getFloorEntry(K key) const {
    if (this->root == nullptr) {
      throw NoSuchMappingException("No floor entry exists in this map");
    }

    NodePtr node = this->root;

    while (node != nullptr) {
      if (key == node->key) {
        return node->entry();
      }

      if (compare(key, node->key)) {
        /* key < node->key */
        if (node->left != nullptr) {
          node = node->left;
        } else {
          while (node->direction() == Direction::LEFT) {
            if (node != nullptr) {
              node = node->parent;
            } else {
              throw NoSuchMappingException("No floor entry exists in this map");
            }
          }
          if (node->parent == nullptr) {
            throw NoSuchMappingException("No floor entry exists in this map");
          }
          return node->parent->entry();
        }
      } else {
        /* key > node->key */
        if (node->right != nullptr) {
          node = node->right;
        } else {
          return node->entry();
        }
      }
    }

    throw NoSuchMappingException("No floor entry exists in this map");
  }

  /**
   * Gets the entry for the least key greater than the specified
   * key; if no such entry exists, returns the entry for the least
   * key greater than the specified key; if no such entry exists,
   * a {@code NoSuchMappingException} will be thrown.
   * @param key
   * @return RBTreeMap<Key, Value>::Entry
   * @throws NoSuchMappingException
   */
  Entry getHigherEntry(K key) {
    if (this->root == nullptr) {
      throw NoSuchMappingException("No higher entry exists in this map");
    }

    NodePtr node = this->root;

    while (node != nullptr) {
      if (compare(key, node->key)) {
        /* key < node->key */
        if (node->left != nullptr) {
          node = node->left;
        } else {
          return node->entry();
        }
      } else {
        /* key >= node->key */
        if (node->right != nullptr) {
          node = node->right;
        } else {
          while (node->direction() == Direction::RIGHT) {
            if (node != nullptr) {
              node = node->parent;
            } else {
              throw NoSuchMappingException(
                  "No higher entry exists in this map");
            }
          }
          if (node->parent == nullptr) {
            throw NoSuchMappingException("No higher entry exists in this map");
          }
          return node->parent->entry();
        }
      }
    }

    throw NoSuchMappingException("No higher entry exists in this map");
  }

  /**
   * Returns the entry for the greatest key less than the specified key; if
   * no such entry exists (i.e., the least key in the Tree is greater than
   * the specified key), a {@code NoSuchMappingException} will be thrown.
   * @param key
   * @return RBTreeMap<Key, Value>::Entry
   * @throws NoSuchMappingException
   */
  Entry getLowerEntry(K key) const {
    if (this->root == nullptr) {
      throw NoSuchMappingException("No lower entry exists in this map");
    }

    NodePtr node = this->root;

    while (node != nullptr) {
      if (compare(key, node->key) || key == node->key) {
        /* key <= node->key */
        if (node->left != nullptr) {
          node = node->left;
        } else {
          while (node->direction() == Direction::LEFT) {
            if (node != nullptr) {
              node = node->parent;
            } else {
              throw NoSuchMappingException("No lower entry exists in this map");
            }
          }
          if (node->parent == nullptr) {
            throw NoSuchMappingException("No lower entry exists in this map");
          }
          return node->parent->entry();
        }
      } else {
        /* key > node->key */
        if (node->right != nullptr) {
          node = node->right;
        } else {
          return node->entry();
        }
      }
    }

    throw NoSuchMappingException("No lower entry exists in this map");
  }

  /**
   * Remove all entries that satisfy the filter condition.
   * @param filter
   */
  void removeAll(KeyValueFilter filter) {
    std::vector<Key> keys;
    this->inorderTraversal([&](ConstNodePtr node) {
      if (filter(node->key, node->value)) {
        keys.push_back(node->key);
      }
    });
    for (const Key &key : keys) {
      this->remove(key);
    }
  }

  /**
   * Performs the given action for each key and value entry in this map.
   * The value is immutable for the action.
   * @param action
   */
  void forEach(KeyValueConsumer action) const {
    this->inorderTraversal(
        [&](ConstNodePtr node) { action(node->key, node->value); });
  }

  /**
   * Performs the given action for each key and value entry in this map.
   * The value is mutable for the action.
   * @param action
   */
  void forEachMut(MutKeyValueConsumer action) {
    this->inorderTraversal(
        [&](ConstNodePtr node) { action(node->key, node->value); });
  }

  /**
   * Returns a list containing all of the entries in this map.
   * @return RBTreeMap<Key, Value>::EntryList
   */
  EntryList toEntryList() const {
    EntryList entryList;
    this->inorderTraversal(
        [&](ConstNodePtr node) { entryList.push_back(node->entry()); });
    return entryList;
  }

 private:
  static void maintainRelationship(ConstNodePtr node) {
    if (node->left != nullptr) {
      node->left->parent = node;
    }
    if (node->right != nullptr) {
      node->right->parent = node;
    }
  }

  static void swapNode(NodePtr &lhs, NodePtr &rhs) {
    std::swap(lhs->key, rhs->key);
    std::swap(lhs->value, rhs->value);
    std::swap(lhs, rhs);
  }

  void rotateLeft(ConstNodePtr node) {
    // clang-format off
    //     |                       |
    //     N                       S
    //    / \     l-rotate(N)     / \
    //   L   S    ==========>    N   R
    //      / \                 / \
    //     M   R               L   M
    assert(node != nullptr && node->right != nullptr);
    // clang-format on
    NodePtr parent = node->parent;
    Direction direction = node->direction();

    NodePtr successor = node->right;
    node->right = successor->left;
    successor->left = node;

    maintainRelationship(node);
    maintainRelationship(successor);

    switch (direction) {
      case Direction::ROOT:
        this->root = successor;
        break;
      case Direction::LEFT:
        parent->left = successor;
        break;
      case Direction::RIGHT:
        parent->right = successor;
        break;
    }

    successor->parent = parent;
  }

  void rotateRight(ConstNodePtr node) {
    // clang-format off
    //       |                   |
    //       N                   S
    //      / \   r-rotate(N)   / \
    //     S   R  ==========>  L   N
    //    / \                     / \
    //   L   M                   M   R
    assert(node != nullptr && node->left != nullptr);
    // clang-format on

    NodePtr parent = node->parent;
    Direction direction = node->direction();

    NodePtr successor = node->left;
    node->left = successor->right;
    successor->right = node;

    maintainRelationship(node);
    maintainRelationship(successor);

    switch (direction) {
      case Direction::ROOT:
        this->root = successor;
        break;
      case Direction::LEFT:
        parent->left = successor;
        break;
      case Direction::RIGHT:
        parent->right = successor;
        break;
    }

    successor->parent = parent;
  }

  inline void rotateSameDirection(ConstNodePtr node, Direction direction) {
    assert(direction != Direction::ROOT);
    if (direction == Direction::LEFT) {
      rotateLeft(node);
    } else {
      rotateRight(node);
    }
  }

  inline void rotateOppositeDirection(ConstNodePtr node, Direction direction) {
    assert(direction != Direction::ROOT);
    if (direction == Direction::LEFT) {
      rotateRight(node);
    } else {
      rotateLeft(node);
    }
  }

  void maintainAfterInsert(NodePtr node) {
    assert(node != nullptr);

    if (node->isRoot()) {
      // Case 1: Current node is root (RED)
      //  No need to fix.
      assert(node->isRed());
      return;
    }

    if (node->parent->isBlack()) {
      // Case 2: Parent is BLACK
      //  No need to fix.
      return;
    }

    if (node->parent->isRoot()) {
      // clang-format off
      // Case 3: Parent is root and is RED
      //   Paint parent to BLACK.
      //    <P>         [P]
      //     |   ====>   |
      //    <N>         <N>
      //   p.s.
      //    `<X>` is a RED node;
      //    `[X]` is a BLACK node (or NIL);
      //    `{X}` is either a RED node or a BLACK node;
      // clang-format on
      assert(node->parent->isRed());
      node->parent->color = Node::BLACK;
      return;
    }

    if (node->hasUncle() && node->uncle()->isRed()) {
      // clang-format off
      // Case 4: Both parent and uncle are RED
      //   Paint parent and uncle to BLACK;
      //   Paint grandparent to RED.
      //        [G]             <G>
      //        / \             / \
      //      <P> <U>  ====>  [P] [U]
      //      /               /
      //    <N>             <N>
      // clang-format on
      assert(node->parent->isRed());
      node->parent->color = Node::BLACK;
      node->uncle()->color = Node::BLACK;
      node->grandParent()->color = Node::RED;
      maintainAfterInsert(node->grandParent());
      return;
    }

    if (!node->hasUncle() || node->uncle()->isBlack()) {
      // Case 5 & 6: Parent is RED and Uncle is BLACK
      //   p.s. NIL nodes are also considered BLACK
      assert(!node->isRoot());

      if (node->direction() != node->parent->direction()) {
        // clang-format off
        // Case 5: Current node is the opposite direction as parent
        //   Step 1. If node is a LEFT child, perform l-rotate to parent;
        //           If node is a RIGHT child, perform r-rotate to parent.
        //   Step 2. Goto Case 6.
        //      [G]                 [G]
        //      / \    rotate(P)    / \
        //    <P> [U]  ========>  <N> [U]
        //      \                 /
        //      <N>             <P>
        // clang-format on

        // Step 1: Rotation
        NodePtr parent = node->parent;
        if (node->direction() == Direction::LEFT) {
          rotateRight(node->parent);
        } else /* node->direction() == Direction::RIGHT */ {
          rotateLeft(node->parent);
        }
        node = parent;
        // Step 2: vvv
      }

      // clang-format off
      // Case 6: Current node is the same direction as parent
      //   Step 1. If node is a LEFT child, perform r-rotate to grandparent;
      //           If node is a RIGHT child, perform l-rotate to grandparent.
      //   Step 2. Paint parent (before rotate) to BLACK;
      //           Paint grandparent (before rotate) to RED.
      //        [G]                 <P>               [P]
      //        / \    rotate(G)    / \    repaint    / \
      //      <P> [U]  ========>  <N> [G]  ======>  <N> <G>
      //      /                         \                 \
      //    <N>                         [U]               [U]
      // clang-format on

      assert(node->grandParent() != nullptr);

      // Step 1
      if (node->parent->direction() == Direction::LEFT) {
        rotateRight(node->grandParent());
      } else {
        rotateLeft(node->grandParent());
      }

      // Step 2
      node->parent->color = Node::BLACK;
      node->sibling()->color = Node::RED;

      return;
    }
  }

  NodePtr getNodeOrProvide(NodePtr &node, K key, NodeProvider provide) {
    assert(node != nullptr);

    if (key == node->key) {
      return node;
    }

    assert(key != node->key);

    NodePtr result;

    if (compare(key, node->key)) {
      /* key < node->key */
      if (node->left == nullptr) {
        result = node->left = provide();
        node->left->parent = node;
        maintainAfterInsert(node->left);
        this->count += 1;
      } else {
        result = getNodeOrProvide(node->left, key, provide);
      }
    } else {
      /* key > node->key */
      if (node->right == nullptr) {
        result = node->right = provide();
        node->right->parent = node;
        maintainAfterInsert(node->right);
        this->count += 1;
      } else {
        result = getNodeOrProvide(node->right, key, provide);
      }
    }

    return result;
  }

  NodePtr getNode(ConstNodePtr node, K key) const {
    assert(node != nullptr);

    if (key == node->key) {
      return node;
    }

    if (compare(key, node->key)) {
      /* key < node->key */
      return node->left == nullptr ? nullptr : getNode(node->left, key);
    } else {
      /* key > node->key */
      return node->right == nullptr ? nullptr : getNode(node->right, key);
    }
  }

  void insert(NodePtr &node, K key, V value, bool replace = true) {
    assert(node != nullptr);

    if (key == node->key) {
      if (replace) {
        node->value = value;
      }
      return;
    }

    assert(key != node->key);

    if (compare(key, node->key)) {
      /* key < node->key */
      if (node->left == nullptr) {
        node->left = Node::from(key, value);
        node->left->parent = node;
        maintainAfterInsert(node->left);
        this->count += 1;
      } else {
        insert(node->left, key, value, replace);
      }
    } else {
      /* key > node->key */
      if (node->right == nullptr) {
        node->right = Node::from(key, value);
        node->right->parent = node;
        maintainAfterInsert(node->right);
        this->count += 1;
      } else {
        insert(node->right, key, value, replace);
      }
    }
  }

  void maintainAfterRemove(ConstNodePtr node) {
    if (node->isRoot()) {
      return;
    }

    assert(node->isBlack() && node->hasSibling());

    Direction direction = node->direction();

    NodePtr sibling = node->sibling();
    if (sibling->isRed()) {
      // clang-format off
      // Case 1: Sibling is RED, parent and nephews must be BLACK
      //   Step 1. If N is a left child, left rotate P;
      //           If N is a right child, right rotate P.
      //   Step 2. Paint S to BLACK, P to RED
      //   Step 3. Goto Case 2, 3, 4, 5
      //      [P]                   <S>               [S]
      //      / \    l-rotate(P)    / \    repaint    / \
      //    [N] <S>  ==========>  [P] [D]  ======>  <P> [D]
      //        / \               / \               / \
      //      [C] [D]           [N] [C]           [N] [C]
      // clang-format on
      ConstNodePtr parent = node->parent;
      assert(parent != nullptr && parent->isBlack());
      assert(sibling->left != nullptr && sibling->left->isBlack());
      assert(sibling->right != nullptr && sibling->right->isBlack());
      // Step 1
      rotateSameDirection(node->parent, direction);
      // Step 2
      sibling->color = Node::BLACK;
      parent->color = Node::RED;
      // Update sibling after rotation
      sibling = node->sibling();
      // Step 3: vvv
    }

    NodePtr closeNephew =
        direction == Direction::LEFT ? sibling->left : sibling->right;
    NodePtr distantNephew =
        direction == Direction::LEFT ? sibling->right : sibling->left;

    bool closeNephewIsBlack = closeNephew == nullptr || closeNephew->isBlack();
    bool distantNephewIsBlack =
        distantNephew == nullptr || distantNephew->isBlack();

    assert(sibling->isBlack());

    if (closeNephewIsBlack && distantNephewIsBlack) {
      if (node->parent->isRed()) {
        // clang-format off
        // Case 2: Sibling and nephews are BLACK, parent is RED
        //   Swap the color of P and S
        //      <P>             [P]
        //      / \             / \
        //    [N] [S]  ====>  [N] <S>
        //        / \             / \
        //      [C] [D]         [C] [D]
        // clang-format on
        sibling->color = Node::RED;
        node->parent->color = Node::BLACK;
        return;
      } else {
        // clang-format off
        // Case 3: Sibling, parent and nephews are all black
        //   Step 1. Paint S to RED
        //   Step 2. Recursively maintain P
        //      [P]             [P]
        //      / \             / \
        //    [N] [S]  ====>  [N] <S>
        //        / \             / \
        //      [C] [D]         [C] [D]
        // clang-format on
        sibling->color = Node::RED;
        maintainAfterRemove(node->parent);
        return;
      }
    } else {
      if (closeNephew != nullptr && closeNephew->isRed()) {
        // clang-format off
        // Case 4: Sibling is BLACK, close nephew is RED,
        //         distant nephew is BLACK
        //   Step 1. If N is a left child, right rotate S;
        //           If N is a right child, left rotate S.
        //   Step 2. Swap the color of close nephew and sibling
        //   Step 3. Goto case 5
        //                            {P}                {P}
        //      {P}                   / \                / \
        //      / \    r-rotate(S)  [N] <C>   repaint  [N] [C]
        //    [N] [S]  ==========>        \   ======>        \
        //        / \                     [S]                <S>
        //      <C> [D]                     \                  \
        //                                  [D]                [D]
        // clang-format on

        // Step 1
        rotateOppositeDirection(sibling, direction);
        // Step 2
        closeNephew->color = Node::BLACK;
        sibling->color = Node::RED;
        // Update sibling and nephews after rotation
        sibling = node->sibling();
        closeNephew =
            direction == Direction::LEFT ? sibling->left : sibling->right;
        distantNephew =
            direction == Direction::LEFT ? sibling->right : sibling->left;
        // Step 3: vvv
      }

      // clang-format off
      // Case 5: Sibling is BLACK, distant nephew is RED
      //   Step 1. If N is a left child, left rotate P;
      //           If N is a right child, right rotate P.
      //   Step 2. Swap the color of parent and sibling.
      //   Step 3. Paint distant nephew D to BLACK.
      //      {P}                   [S]               {S}
      //      / \    l-rotate(P)    / \    repaint    / \
      //    [N] [S]  ==========>  {P} <D>  ======>  [P] [D]
      //        / \               / \               / \
      //      {C} <D>           [N] {C}           [N] {C}
      // clang-format on
      assert(distantNephew->isRed());
      // Step 1
      rotateSameDirection(node->parent, direction);
      // Step 2
      sibling->color = node->parent->color;
      node->parent->color = Node::BLACK;
      if (distantNephew != nullptr) {
        distantNephew->color = Node::BLACK;
      }
      return;
    }
  }

  bool remove(NodePtr node, K key, NodeConsumer action) {
    assert(node != nullptr);

    if (key != node->key) {
      if (compare(key, node->key)) {
        /* key < node->key */
        NodePtr &left = node->left;
        if (left != nullptr && remove(left, key, action)) {
          maintainRelationship(node);
          return true;
        } else {
          return false;
        }
      } else {
        /* key > node->key */
        NodePtr &right = node->right;
        if (right != nullptr && remove(right, key, action)) {
          maintainRelationship(node);
          return true;
        } else {
          return false;
        }
      }
    }

    assert(key == node->key);
    action(node);

    if (this->size() == 1) {
      // Current node is the only node of the tree
      this->clear();
      return true;
    }

    if (node->left != nullptr && node->right != nullptr) {
      // clang-format off
      // Case 1: If the node is strictly internal
      //   Step 1. Find the successor S with the smallest key
      //           and its parent P on the right subtree.
      //   Step 2. Swap the data (key and value) of S and N,
      //           S is the node that will be deleted in place of N.
      //   Step 3. N = S, goto Case 2, 3
      //     |                    |
      //     N                    S
      //    / \                  / \
      //   L  ..   swap(N, S)   L  ..
      //       |   =========>       |
      //       P                    P
      //      / \                  / \
      //     S  ..                N  ..
      // clang-format on

      // Step 1
      NodePtr successor = node->right;
      NodePtr parent = node;
      while (successor->left != nullptr) {
        parent = successor;
        successor = parent->left;
      }
      // Step 2
      swapNode(node, successor);
      maintainRelationship(parent);
      // Step 3: vvv
    }

    if (node->isLeaf()) {
      // Current node must not be the root
      assert(node->parent != nullptr);

      // Case 2: Current node is a leaf
      //   Step 1. Unlink and remove it.
      //   Step 2. If N is BLACK, maintain N;
      //           If N is RED, do nothing.

      // The maintain operation won't change the node itself,
      //  so we can perform maintain operation before unlink the node.
      if (node->isBlack()) {
        maintainAfterRemove(node);
      }
      if (node->direction() == Direction::LEFT) {
        node->parent->left = nullptr;
      } else /* node->direction() == Direction::RIGHT */ {
        node->parent->right = nullptr;
      }
    } else /* !node->isLeaf() */ {
      assert(node->left == nullptr || node->right == nullptr);
      // Case 3: Current node has a single left or right child
      //   Step 1. Replace N with its child
      //   Step 2. If N is BLACK, maintain N
      NodePtr parent = node->parent;
      NodePtr replacement = (node->left != nullptr ? node->left : node->right);
      switch (node->direction()) {
        case Direction::ROOT:
          this->root = replacement;
          break;
        case Direction::LEFT:
          parent->left = replacement;
          break;
        case Direction::RIGHT:
          parent->right = replacement;
          break;
      }

      if (!node->isRoot()) {
        replacement->parent = parent;
      }

      if (node->isBlack()) {
        if (replacement->isRed()) {
          replacement->color = Node::BLACK;
        } else {
          maintainAfterRemove(replacement);
        }
      }
    }

    this->count -= 1;
    return true;
  }

  void inorderTraversal(NodeConsumer action) const {
    if (this->root == nullptr) {
      return;
    }

    std::stack<NodePtr> stack;
    NodePtr node = this->root;

    while (node != nullptr || !stack.empty()) {
      while (node != nullptr) {
        stack.push(node);
        node = node->left;
      }
      if (!stack.empty()) {
        node = stack.top();
        stack.pop();
        action(node);
        node = node->right;
      }
    }
  }
};

#endif  // RBTREE_MAP_HPP

七、小结：红黑树的实战优势

特性	红黑树	AVL 树	B 树/B+ 树
平衡性	较强	最强	中等（多路）
操作复杂度	O(log n)	O(log n)	O(log n)
插入旋转次数	≤ 2	≤ log n	无旋转
应用场景	操作系统、语言库、Java集合类	内存优先	数据库、磁盘结构