动手学深度学习 - 优化算法 - 12.2 凸性-CSDN博客

本文链接：https://blog.csdn.net/tang7mj/article/details/148295687

动手学深度学习 - 优化算法 - 12.2 凸性

凸性（Convexity）是优化算法中最重要的数学基础之一。尽管深度学习中的优化问题通常是非凸的，但很多时候，它们在局部区域近似凸，这使得很多凸优化的结论与技术仍然具有指导意义。学习凸性不仅帮助我们理解优化算法的收敛行为，还为理论分析和新算法设计打下基础。

12.2.1 定义

12.2.1.1 凸集

我们首先定义凸集。简单来说，一个集合是凸的，当你在集合中任选两个点，它们之间连成的整条线段也仍然完全包含在这个集合中。

数学表达式如下：

这可能听起来有点抽象，所以我们通过图 12.2.1 来直观理解它：

左边那个像吃豆人的图形就不是凸的，因为两个点之间的线段穿出了集合；
中间和右边两个集合则是凸的。

定义凸集的意义在于，它们对优化问题具有良好性质。例如，凸集的交集仍然是凸的，但并集不一定是凸的，如图 12.2.2 与图 12.2.3 所示。

12.2.1.2 凸函数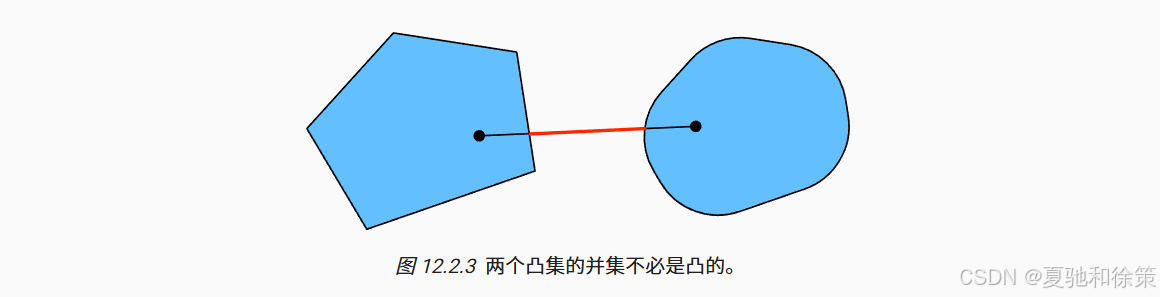

定义完凸集，我们就可以定义凸函数。给定一个定义在凸集上的函数 ff，如果对于任意两点 x,x′∈Xx, x' \in \mathcal{X}，满足：

我们就称 ff 是凸函数。

图中展示了几个典型函数：

抛物线和指数函数是凸的；
余弦函数则不是凸函数，因为其连线会穿出函数图像上方。

12.2.1.3 詹森不等式

詹森不等式是凸函数的重要性质：

也就是说，凸函数作用在期望上总小于或等于将其作用到样本再求期望。这一不等式在变分推理、EM 算法等场景中尤为常见。

12.2.2 凸函数的性质

12.2.2.1 局部最小值也是全局最小值

这是凸函数最重要的性质之一：

对于凸函数，只要一个点是局部最小值，它一定也是全局最小值。

这个性质意味着，我们不会被“困在”某个差的局部最小值里。图示函数 f(x)=(x−1)2f(x) = (x - 1)^2 在 x=1x=1 处有唯一最小值，即局部也是全局。

12.2.2.2 下水平集是凸集

对于一个凸函数 ff，其下水平集：

是一个凸集。这一性质对约束优化尤为重要。

12.2.2.3 凸性与二阶导数

判断一个函数是否是凸的最常用方法是：

如果函数二阶可导，且其 Hessian 矩阵是正半定（所有特征值非负），那么函数就是凸的。

对于一维函数，这简化为：

多维情况则需检查：

12.2.3 凸约束与优化策略

凸优化一个非常好的性质就是：

只要目标函数是凸的，约束也是凸的，那么整个问题就能高效求解。

我们通常写成：

12.2.3.1 拉格朗日乘子法

通过拉格朗日函数 L(x,λ,ν)\mathcal{L}(x, \lambda, \nu)，我们将约束优化转化为鞍点问题：

在深度学习中，它常用于软约束和对偶优化，如 SVM。

12.2.3.2 罚函数法（Penalty）

我们可将约束写入目标函数中，加上罚项：

例如权重衰减（L2 正则化）就是一种典型的罚函数策略，用于控制参数范围。

12.2.3.3 投影（Projection）

另一种方法是：每次参数更新后，将其投影回凸集内，保证约束始终满足：

如图 12.2.4，点被投影到球或菱形内，确保满足凸集约束。

🎓 理论理解

凸集 = 连线全在集内；凸函数 = 图像在弦线下方
- 凸集定义强调几何意义，是优化问题的“搜索空间”；
- 凸函数定义强调函数形状，是目标函数“山谷形态”的刻画；
- 两者共同构成“好优化问题”的充分条件。
局部最小 = 全局最小 ⇒ 搜索路径更安全
在凸函数下，任何局部最小值都是全局最小值。这意味着我们可以放心地使用梯度下降这类“只看当前方向”的贪心算法，不用担心陷入次优坑。
Hessian 正半定 ⇔ 函数凸性（连续可导条件下）
数学上最常用的判断标准是：
- 一维函数 f′′(x)≥0f''(x) \geq 0f′′(x)≥0；
- 多维函数 Hessian 矩阵正半定，即所有特征值非负。
Jensen 不等式连接了概率与优化
Jensen 不等式将凸性从几何推广到了概率空间，是贝叶斯推断、变分方法、最大期望算法（EM）中的理论核心。
凸优化的三种约束处理方式互有取舍：
- 拉格朗日法：结构严谨，适合分析解推导；
- 罚项法：灵活稳健，适合深度学习中软约束；
- 投影法：可控收敛，常用于梯度裁剪、范数控制等。

🏭 工程实践理解（以 Google / Meta / 字节跳动为参考）

Google & NVIDIA：用“投影 + 正则”稳健训练大模型
在大模型（如 GPT、BERT、ViT）训练中，工程团队会引入：
- 梯度范数投影（例如最大值裁剪到 L2 Ball）；
- 权重正则化（L2 罚项即 soft constraint）；
- Warmup + Cosine Decay 的学习率调度；
  这些操作虽不明说“凸”，但本质都与凸约束投影或惩罚优化有关。
字节跳动：在推荐模型中用 Jensen 不等式构造变分下界
在 CTR、CVR 模型中，为了解决隐变量带来的对数似然不可解析问题，会使用 Jensen 不等式引入变分下界，使优化目标可计算。
Meta：在 Meta-Learning 中引入凸正则项，约束模型迁移稳定性
多任务学习中，为防止模型过拟合每个任务，会用 convex loss + convex regularizer（如 KL 距离、entropy bounds）构造组合目标函数，确保解空间稳定。
常见误区避免：
- 并不是所有“看起来像碗”的函数都是凸的，要看定义域；
- L1 正则虽然不是严格凸，但仍然能诱导稀疏解；
- 投影方法要搭配梯度更新，否则会产生“折返”行为。

🧠 大厂面试题：12.2 凸性

✅ 面试题 1【基础理论题】

Q：什么是凸函数？请写出数学定义，并说明它与优化问题中的全局最优解有何关系。

参考答案：
一个函数 ff 定义在一个凸集上，如果满足对任意 x,x′∈Xx, x' \in \mathcal{X} 和 λ∈[0,1]\lambda \in [0,1]：

则 ff 是凸函数。在优化中，这一性质意味着局部最小值一定是全局最小值，因此搜索过程可以放心地使用局部算法（如梯度下降）。

✅ 面试题 2【判断与推导题】

Q：如何判断一个连续可导的函数是凸函数？多维情况下该如何判断？

参考答案：

一维情况下：若 f′′(x)≥0f''(x) \geq 0，则 ff 是凸的；

多维情况下：若 ∇2f(x)\nabla^2 f(x) 是正半定矩阵（所有特征值 ≥0\geq 0），则 ff 是凸函数；

正半定可通过判断 z⊤∇2f(x)z≥0, ∀zz^\top \nabla^2 f(x) z \geq 0,\ \forall z 来验证。

✅ 面试题 3【应用场景题】

Q：你正在训练一个带 L2 正则项的深度模型，这个正则项是否改变了目标函数的凸性？为什么？

参考答案：
L2 正则项（如 λ∥w∥22\lambda \|w\|_2^2）本身是凸函数；如果原始损失函数也是凸的（如 MSE），则加上 L2 正则之后仍是凸的，因为凸函数的加法仍为凸函数；但如果原始损失非凸，加正则项无法保证整体凸性。

✅ 面试题 4【Jensen 不等式题】

Q：写出 Jensen 不等式，并说明它在深度学习中一个常见应用场景。

参考答案：
Jensen 不等式：对凸函数 ff，有

应用场景：在变分自编码器（VAE）或 EM 算法中，用 Jensen 不等式推导变分下界，使对数似然函数近似可优化。

✅ 面试题 5【投影操作】

Q：什么是凸集上的投影？它在深度学习中有哪些实际用法？

参考答案：
凸集 X\mathcal{X} 上对点 xx 的投影定义为：

作用是将点强制限制在可行区域内；
工程中常用于：

梯度裁剪（clip to L2 Ball）；

参数范数约束；

训练阶段的可行域投影（如强化学习的 action clipping）。

✅ 面试题 6【开放性思考题】

Q：为什么大多数深度学习优化问题是非凸的？我们为什么仍然能“训练得很好”？

参考思路：

深度模型由非线性组合（如 ReLU、BatchNorm）构成，导致整体目标函数非凸；

但在训练过程中，参数路径局部可能呈现近似凸性；

加之现代优化器（如 Adam、SGD+momentum）+ 初始策略 + 正则技术，使得即便非凸，仍能找到“好解”。

场景题（12.2 凸性）

📌 场景题 1：字节跳动推荐算法团队 - CVR 多任务模型失稳

背景：
你在字节跳动的广告推荐系统中参与训练一个包含 CTR（点击率）和 CVR（转化率）联合建模的多任务网络。近期业务方反馈模型在某些类目下性能波动严重，经检查发现 loss 曲线波动异常，有时甚至 loss < 0。

任务描述：
请判断是否可能是 loss 函数设计或优化空间不具备凸性 导致不稳定？你会如何进行理论分析与工程验证？

要求：

判断原始 loss 函数（如 logloss + 加权 sum）是否为凸函数；
提出是否可以通过调整 loss 结构或加入 convex regularizer 提升训练稳定性；
是否可以使用 Jensen 不等式推导出某种更鲁棒的下界替代优化目标？

📌 场景题 2：阿里达摩院视觉模型 - 优化路径陷入非凸局部最小值

背景：
你在阿里视觉团队训练一个多分支的图像风格转换网络，损失函数包括内容损失、风格损失和感知损失。训练过程中发现模型性能高度依赖初始化，稍有扰动便陷入较差的解，推测是由于目标函数强非凸性导致。

任务描述：
你作为优化专家，如何运用凸分析工具来分析 loss surface 并重构目标函数的优化路径？

要求：

判断是否存在在局部区域近似凸的可能；
提出如何通过投影策略或添加 convex component（如 L2 正则、TV loss）构造更“凸”的优化区域；
可否通过可视化（如 Hessian 特征谱、loss landscape）分析当前非凸性程度？

📌 场景题 3：Google Research - 变分自编码器中的 Jensen 不等式设计

背景：
你参与 Google Brain 团队的一项图像生成项目，采用变分自编码器（VAE）训练结构图模型，目标是最大化数据的对数似然，但由于存在隐变量 Z，该对数似然无法直接求解。

任务描述：
你需要推导一个优化目标函数，使其既可导、可优化，又满足一定理论上界。

要求：

请写出如何使用 Jensen 不等式构造 Evidence Lower Bound（ELBO）；
解释 ELBO 函数的凸性与优化稳定性的关系；
如果原始问题是非凸的，你是否可以将目标函数改写为局部凸函数组合？

📌 场景题 4：NVIDIA Jetson 边缘端部署 - 模型参数投影优化策略

背景：
你负责 Jetson Nano 平台上部署一个嵌入式目标检测模型。由于设备内存小、计算限制多，模型权重大小和梯度更新必须严格控制。

任务描述：
每次权重更新后，你需将参数投影到约束空间中，以防止模型过拟合和溢出。

要求：

如何在训练中引入凸投影策略来强制模型参数满足 L2 范数不超过某阈值？
如何实现这一步的高效投影（考虑批量更新）？
请说明投影策略与凸集几何之间的关系（参考图 12.2.4）？

📌 场景题 5：百度 Apollo 自动驾驶 - 规划模块中的凸优化路径搜索

背景：
你在 Apollo 自动驾驶系统中负责轨迹规划模块。车辆需要在障碍物之间寻找一条最优路径，该路径必须是连续、平滑且避开所有障碍。

任务描述：
请用凸优化方法构造轨迹搜索模型，保障轨迹的安全性与可解性。

要求：

目标函数是否可以构造成 convex（如最短路径 + 平滑度惩罚）？
障碍物是否能被定义为 convex constraint（如凸多边形）？
若加速度、曲率等约束存在，如何使用 Lagrangian 乘子法或 penalty 策略整合这些约束？

✅ 总结

这些大厂场景题体现出一个共性：即使深度学习整体是非凸问题，凸性依然是设计高效优化算法的理论支柱与工程落地手段。

应用场景	凸性作用
推荐系统	构造更鲁棒的损失下界（Jensen）
图像生成	构建变分优化目标，保证可优化性
边缘部署	投影权重参数，控制模型范数
自动驾驶规划	用 convex cost + constraints 建模

✅ 总结

考点	常见题型	对应章节内容
凸函数定义	数学公式书写题	12.2.1.2
凸性的判断标准	二阶导数推导、Hessian 特征值判断	12.2.2.3
Jensen 不等式	推导题、变分下界场景题	12.2.1.3
投影方法	工程应用题（梯度裁剪、参数限制）	12.2.3.3
凸约束处理	拉格朗日法、罚项法、投影策略	12.2.3