文章目录
1 引言
因果推断,我又回来啦!
上一篇写的双重机器学习算法(DML)虽然有点小问题(后已在对应的知乎文章上修正),但是依然收获了7K+的阅读量,以及成百上千的关注。想到自己在学习因果推断时的总结和认知能给大家带来一些启发,还是非常开心的。
今天要分享的主题是倾向得分匹配(Propensity Score Matching,PSM)。 如果说DML展现的是流行性,那么PSM透露的就是古典美。同时研究清楚这两类方法,对理解因果推断这个学科方向,是非常有价值的。
在正文开始之前,给大家强烈推荐一个PSM的学习视频。从个人体验来说,这个视频的博主在讲解因果推断的相关视频中,条理清楚且细致入微,让人听了后感觉受益匪浅。这篇文章中的很多内容也是从该系列视频中学习到的,感兴趣的同学可以关注一下。
正文见下。
2 PSM算法原理
2.1 基本问题
PSM本身研究的是匹配问题,但仅做匹配的意义有限,所以我更愿意把PSM放到潜在结果框架下的因果推断问题中去。
首先定义:样本数据集为 D = { d 1 , d 2 , . . . , d n } D=\{d_1,d_2,...,d_n\} D={d1,d2,...,dn}, n n n为样本数量;策略变量为 t ∈ { 0 , 1 } t\in \{0, 1\} t∈{0,1}, t = 0 t=0 t=0表示不施加策略, t = 1 t=1 t=1表示施加策略;协变量 X X X,一般指与策略无关的变量;结果变量 Y Y Y, Y 0 i Y_{0i} Y0i表示不施加策略时第 i i i个样本的结果变量, Y 1 i Y_{1i} Y1i表示施加策略后第 i i i个样本的结果变量。
那么在潜在因果框架下,问题可以描述为:基于数据集 D = { t i , X i , Y i } i n D=\{t_i,X_i,Y_i\}_i^n D={ti,Xi,Yi}in,估计 t t t和 Y Y Y之间的因果效应值。
2.2 算法原理
对于任意样本
i
i
i,根据是否施加策略,可以将潜在结果分为2类:可以实际观测到的
Y
1
i
∣
t
=
1
Y_{1i}|t=1
Y1i∣t=1、
Y
0
i
∣
t
=
0
Y_{0i}|t=0
Y0i∣t=0,和无法实际观测到的
Y
1
i
∣
t
=
0
Y_{1i}|t=0
Y1i∣t=0、
Y
0
i
∣
t
=
1
Y_{0i}|t=1
Y0i∣t=1。
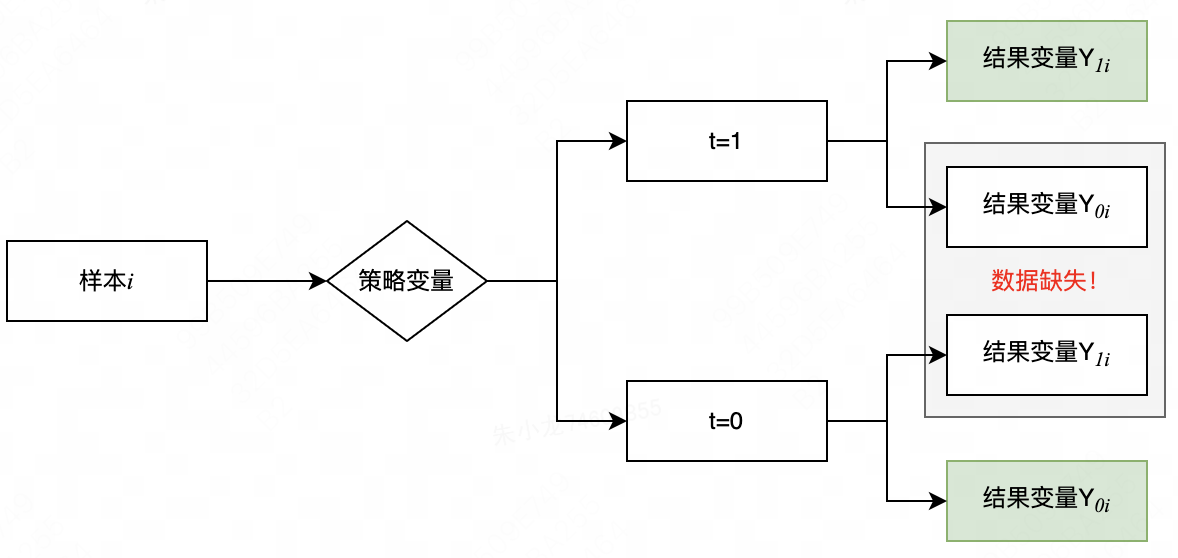
如果直接使用
Y
1
i
∣
t
=
1
Y_{1i}|t=1
Y1i∣t=1减去
Y
0
i
∣
t
=
0
Y_{0i}|t=0
Y0i∣t=0作为
t
=
1
t=1
t=1时的平均因果效应
A
T
T
ATT
ATT,可以做如下推导
A
T
T
=
E
(
Y
1
∣
t
=
1
)
−
E
(
Y
0
∣
t
=
0
)
=
[
E
(
Y
1
∣
t
=
1
)
−
E
(
Y
0
∣
t
=
1
)
]
+
[
E
(
Y
0
∣
t
=
1
)
−
E
(
Y
0
∣
t
=
0
)
]
ATT=E(Y_1|t=1) - E(Y_0|t=0) = [E(Y_1|t=1) - E(Y_0|t=1)] + [E(Y_0|t=1) - E(Y_0|t=0)]
ATT=E(Y1∣t=1)−E(Y0∣t=0)=[E(Y1∣t=1)−E(Y0∣t=1)]+[E(Y0∣t=1)−E(Y0∣t=0)]
前一项显然就是
A
T
T
ATT
ATT的真值,而后一项可以理解为
t
=
1
t=1
t=1和
t
=
0
t=0
t=0间的选择偏差。
在潜在结果框架的基础知识中已经提到,随机实验数据中的 t t t和 Y Y Y无关,所以 E ( Y 0 ∣ t = 1 ) = E ( Y 0 ∣ t = 0 ) E(Y_0|t=1) = E(Y_0|t=0) E(Y0∣t=1)=E(Y0∣t=0)。但是在观测数据里, t t t和 Y Y Y很有可能是相关的,那么我们该如何去除选择偏差呢?
一个很容易想到的思路是:针对 t = 1 t=1 t=1中的每一个样本,都在 t = 0 t=0 t=0中匹配出一个完全一致的样本,此时两者之间便无选择偏差,上式的计算也就没有问题了。在这个思路下,最核心的问题转变为如何在 t = 0 t=0 t=0中找到与 t = 1 t=1 t=1完全一致的样本。
如果影响样本间是否有差异的特征(协变量)只有 1 1 1个,那么按照 t = 1 t=1 t=1样本中该特征的值在 t = 0 t=0 t=0中寻找出相同特征值对应的样本就万事大吉了;但如果协变量数量变多,不仅寻找相同样本的复杂度会增加许多,而且很有可能找不到每个协变量都完全相同的样本。
此时,就是PSM发挥作用的时候了。
PSM告诉我们:如果控制了一组协变量 X X X之后, t t t和 Y Y Y是无关的;那么我们可以根据 X X X构造倾向得分 P P P,且在控制了倾向得分后, t t t和 Y Y Y也是无关的。也就是说,只要倾向得分相同,上式中的选择偏差也可以被去除。
这里需要理解一下倾向得分的含义
P
(
X
)
=
P
r
(
t
=
1
∣
X
)
P(X)=Pr(t=1|X)
P(X)=Pr(t=1∣X)
即在给定协变量
X
X
X后,样本被施加策略的概率。一般情况下,我们可以使用逻辑回归模型来计算倾向得分值。
PSM的优势还是很明显的:它把一组协变量 X X X的匹配问题降维至一个倾向得分值的匹配问题,极大降低了匹配的复杂度。
2.3 原理推导
这么有价值的一个结论,是很值得我们去了解一下证明全过程的。
PSM可以用数学公式表达为
P
r
(
t
=
1
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
)
=
P
r
(
t
=
1
∣
P
(
X
i
)
)
Pr(t=1|Y_{1i},Y_{0i},P(X_i))=Pr(t=1|P(X_i))
Pr(t=1∣Y1i,Y0i,P(Xi))=Pr(t=1∣P(Xi))
等式左边的含义是:同时控制了
Y
1
i
Y_{1i}
Y1i、
Y
0
i
Y_{0i}
Y0i和
P
(
X
i
)
P(X_i)
P(Xi)时
t
=
1
t=1
t=1的概率值;等式右边的含义是:仅控制
P
(
X
i
)
P(X_i)
P(Xi)时
t
=
1
t=1
t=1的概率值。只要两者相等,即意味着
t
t
t和
Y
Y
Y无关。所以接下来的重点是证明上述等式成立。
先看左边的表达式,可以无损地扩展为
P
r
(
t
=
1
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
)
=
P
r
(
t
=
1
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
)
⋅
1
+
P
r
(
t
=
0
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
)
⋅
0
Pr(t=1|Y_{1i},Y_{0i},P(X_i))=Pr(t=1|Y_{1i},Y_{0i},P(X_i))·1 + Pr(t=0|Y_{1i},Y_{0i},P(X_i))·0
Pr(t=1∣Y1i,Y0i,P(Xi))=Pr(t=1∣Y1i,Y0i,P(Xi))⋅1+Pr(t=0∣Y1i,Y0i,P(Xi))⋅0
显然,等式右侧表达式的含义就是期望
E
(
t
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
)
E(t|Y_{1i},Y_{0i},P(X_i))
E(t∣Y1i,Y0i,P(Xi))。这个期望的表达式有点复杂,需要使用如下的期望迭代法则做一下处理
E
(
X
)
=
E
[
E
(
X
∣
Y
)
]
E(X)=E[E(X|Y)]
E(X)=E[E(X∣Y)]
期望迭代法则不是本文的重点,有兴趣的同学可以参考链接:迭代期望定律(law of iterated expectation)是什么?。
如果A是常数,期望迭代法则可以做如下扩展
E
(
X
∣
A
)
=
E
[
E
(
X
∣
Y
)
∣
A
]
E(X|A)=E[E(X|Y)|A]
E(X∣A)=E[E(X∣Y)∣A]
令
X
=
t
,
A
=
Y
1
i
,
Y
0
i
,
P
(
X
i
)
,
Y
=
Y
1
i
,
Y
0
i
,
P
(
X
i
)
,
X
i
X=t, \ A=Y_{1i},Y_{0i},P(X_i), \ Y=Y_{1i},Y_{0i},P(X_i),X_i
X=t, A=Y1i,Y0i,P(Xi), Y=Y1i,Y0i,P(Xi),Xi
E
(
t
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
)
E(t|Y_{1i},Y_{0i},P(X_i))
E(t∣Y1i,Y0i,P(Xi))可以被改写为
E
(
t
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
)
=
E
[
E
(
t
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
,
X
i
)
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
]
E(t|Y_{1i},Y_{0i},P(X_i))=E[E(t|Y_{1i},Y_{0i},P(X_i),X_i)|Y_{1i},Y_{0i},P(X_i)]
E(t∣Y1i,Y0i,P(Xi))=E[E(t∣Y1i,Y0i,P(Xi),Xi)∣Y1i,Y0i,P(Xi)]
由于给定
X
i
X_i
Xi后,
P
(
X
i
)
P(X_i)
P(Xi)就随之确定了,所以上式右侧可以简化为
E
[
E
(
t
∣
Y
1
i
,
Y
0
i
,
X
i
)
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
]
E[E(t|Y_{1i},Y_{0i},X_i)|Y_{1i},Y_{0i},P(X_i)]
E[E(t∣Y1i,Y0i,Xi)∣Y1i,Y0i,P(Xi)]
到了这里,需要使用PSM的前提条件:给定
X
X
X后,
t
t
t和
Y
Y
Y是无关的。所以上式可以简化为
E
[
E
(
t
∣
X
i
)
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
]
E[E(t|X_i)|Y_{1i},Y_{0i},P(X_i)]
E[E(t∣Xi)∣Y1i,Y0i,P(Xi)]
E
(
t
∣
X
i
)
E(t|X_i)
E(t∣Xi)如果使用概率公式展开,由于
t
t
t只有0和1两个取值,所以就只剩下
P
r
(
t
=
1
∣
X
)
Pr(t=1|X)
Pr(t=1∣X),即倾向得分
P
(
X
i
)
P(X_i)
P(Xi)。所以上式可以继续简化
E
[
P
(
X
i
)
∣
Y
1
i
,
Y
0
i
,
P
(
X
i
)
]
E[P(X_i)|Y_{1i},Y_{0i},P(X_i)]
E[P(Xi)∣Y1i,Y0i,P(Xi)]
上式中,要做的事情是:给定
P
(
X
i
)
P(X_i)
P(Xi)后,再求
P
(
X
i
)
P(X_i)
P(Xi)的期望,那自然还是
P
(
X
i
)
P(X_i)
P(Xi)。即PSM的左边表达式等于
P
(
X
i
)
P(X_i)
P(Xi)。
接下来再看一下PSM的右边表达式。
P
r
(
t
=
1
∣
P
(
X
i
)
)
=
P
r
(
t
=
1
∣
P
(
X
i
)
)
⋅
1
+
P
r
(
t
=
0
∣
P
(
X
i
)
)
⋅
0
=
E
(
t
∣
P
(
X
i
)
)
Pr(t=1|P(X_i))=Pr(t=1|P(X_i))·1 + Pr(t=0|P(X_i))·0=E(t|P(X_i))
Pr(t=1∣P(Xi))=Pr(t=1∣P(Xi))⋅1+Pr(t=0∣P(Xi))⋅0=E(t∣P(Xi))
设置期望迭代法则中的参数
X
=
t
,
A
=
P
(
X
i
)
,
Y
=
X
i
X=t,\ A=P(X_i),\ Y=X_i
X=t, A=P(Xi), Y=Xi
可以得到
E
(
t
∣
P
(
X
i
)
)
=
E
(
E
(
t
∣
X
i
)
∣
P
(
X
i
)
)
E(t|P(X_i))=E(E(t|X_i)|P(X_i))
E(t∣P(Xi))=E(E(t∣Xi)∣P(Xi))
E
(
t
∣
X
i
)
E(t|X_i)
E(t∣Xi)刚刚已经推导过了,就是
P
(
X
i
)
P(X_i)
P(Xi),所以得到
E
(
E
(
t
∣
X
i
)
∣
P
(
X
i
)
)
=
E
(
P
(
X
i
)
∣
P
(
X
i
)
)
=
P
(
X
i
)
E(E(t|X_i)|P(X_i))=E(P(X_i)|P(X_i))=P(X_i)
E(E(t∣Xi)∣P(Xi))=E(P(Xi)∣P(Xi))=P(Xi)
即,PSM的右边表达式也等于
P
(
X
i
)
P(X_i)
P(Xi)。
至此,就完成了PSM的证明:控制了倾向得分 P ( X i ) P(X_i) P(Xi), t t t和 Y Y Y无关。
3 PSM做因果推断
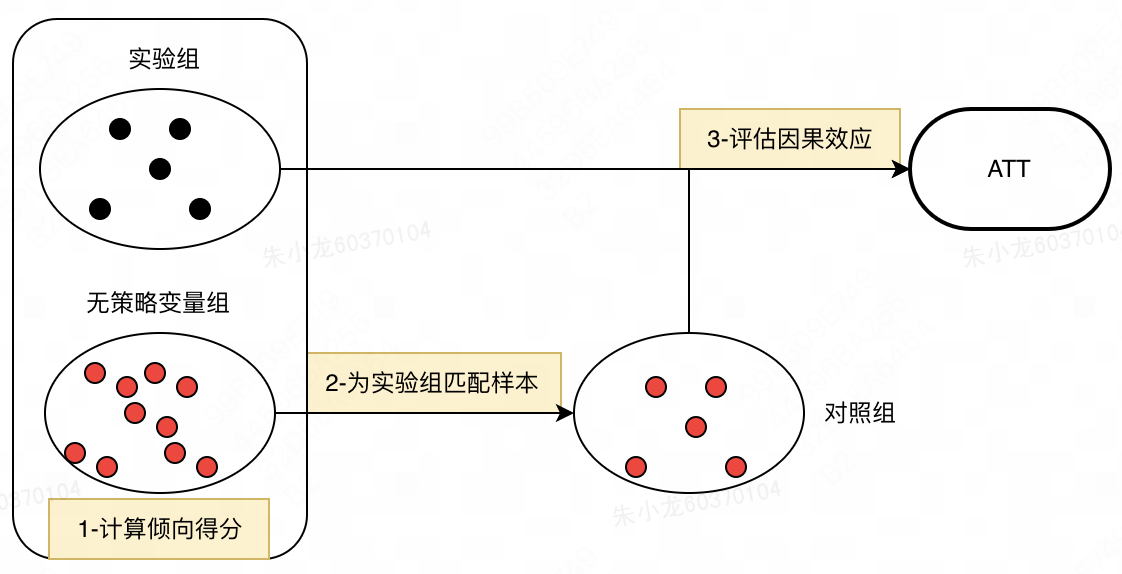
有了PSM原理的加持,使用PSM做因果推断的全流程可以分为三步:
(1) 按照是否施加策略 t t t,将数据集分为实验组 t = 1 t=1 t=1和无策略变量组 t = 0 t=0 t=0。然后计算他们的倾向得分值。
(2) 根据倾向得分值,从无策略变量组中,为实验组中的每个个体匹配出对应的样本,形成对照组。
(3)基于实验组和对照组数据,评估因果效应
A
T
T
ATT
ATT。
4 Stata代码实现
4.1 数据实例
为了能对PSM做因果推断有更深的理解,我们找个实例实践一下。考虑到PSM属于经典算法,很多计量经济学方向的人都使用Stata来调用PSM,本节也采用Stata。
在Stata中,输入指令: use http://ssc.wisc.edu/sscc/pubs/files/psm, replace,可以得到一个
1000
∗
4
1000*4
1000∗4的数据,这个就是本节要使用的实例数据。其中,前两列
x
1
x_1
x1和
x
2
x_2
x2为协变量;第三列
t
t
t为是否施加策略的标志,
1
1
1表示被施加策略,
0
0
0表示未被施加策略;第四列
y
y
y为结果变量值。
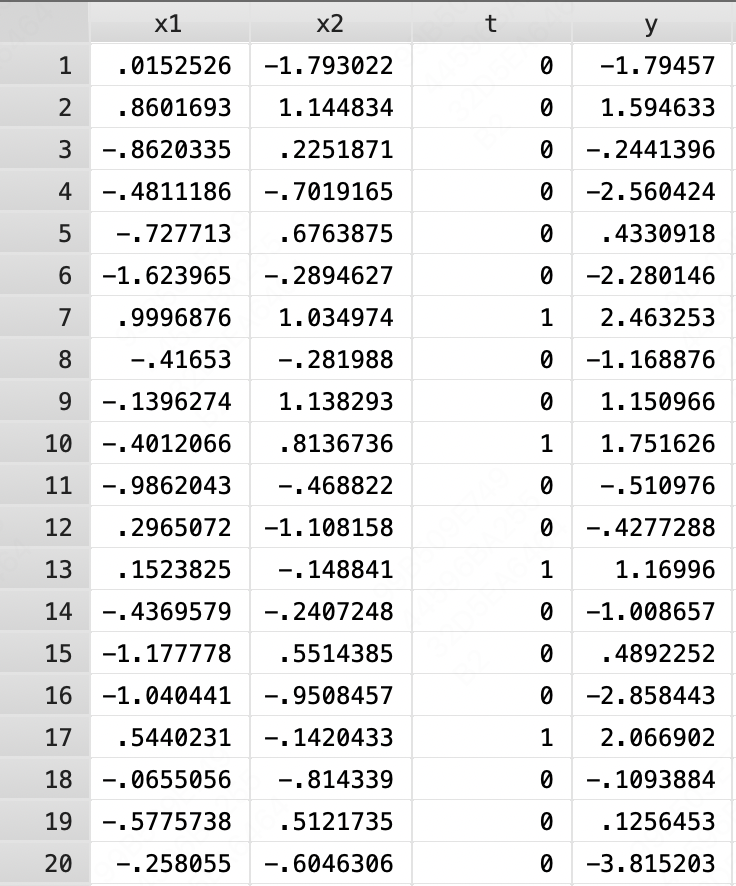
输入指令: psmatch2 t x1 x2, outcome(y) logit n(1),其含义为使用逻辑回归模型计算倾向得分,然后按最近邻匹配策略,从无策略变量组中为每个实验组样本中匹配一个样本,并计算实验组的因果效应
A
T
T
ATT
ATT。下图为Stata直接返回的内容,最核心的内容有两个,第一个是逻辑回归模型的回归参数,第二个是
A
T
T
ATT
ATT的结果。
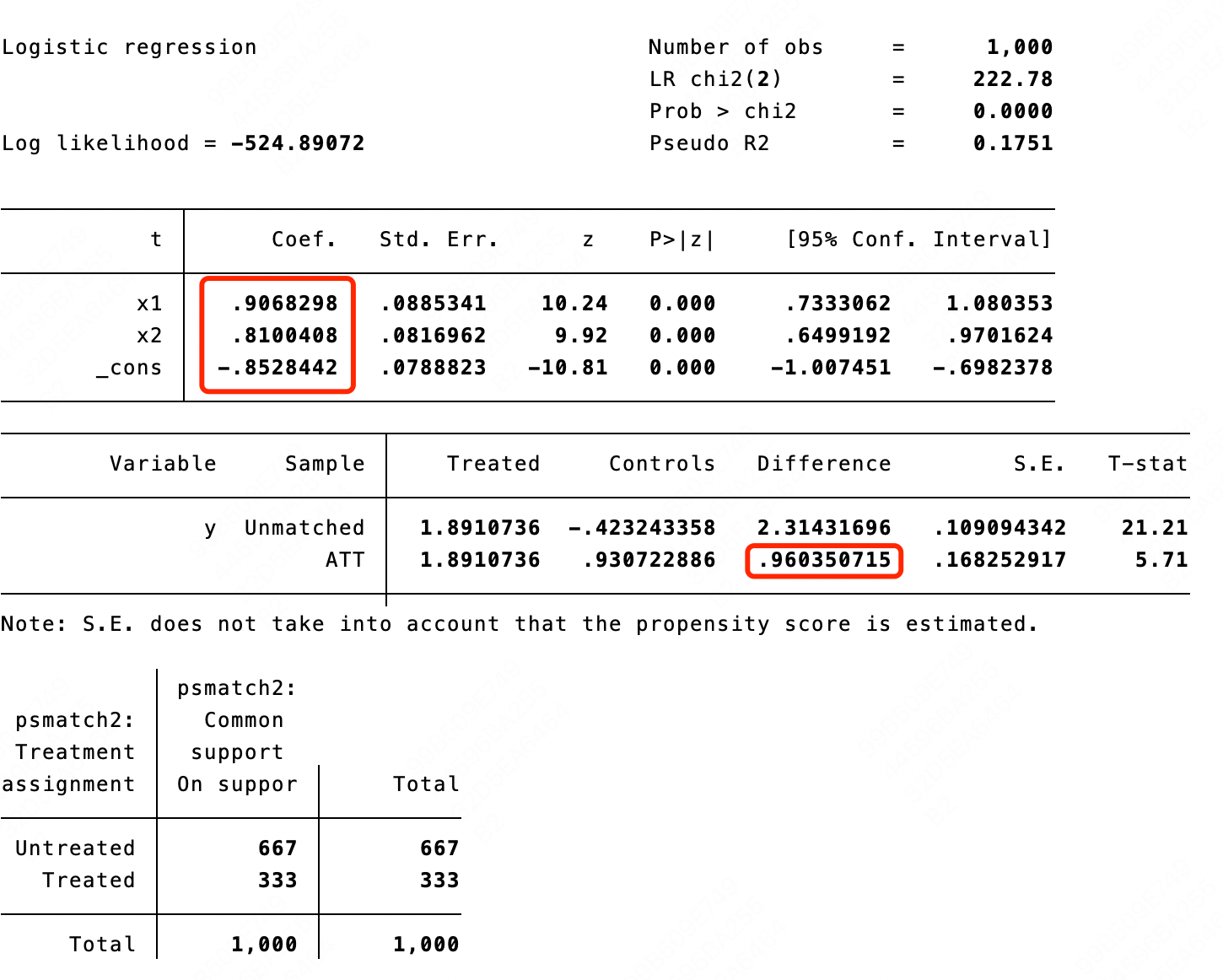
4.2 Stata结果解读
为了更好地理解Stata中的关键结果,我们输入指令:br,查看更多的明细数据。相比原数据,明细数据增加了好多列。我们主要需要关注的是以下4列:
(1) _pscore。每个样本的倾向得分值。
(2) _id。Stata赋予每个样本的一个编号值。计算逻辑是按照_treated列和_pscore列进行排序,然后从 1 1 1开始赋值,逐渐增加。
(3) _n1。为实验组个体匹配的样本所对应的_id值。
(4) _y。匹配样本的结果变量值。
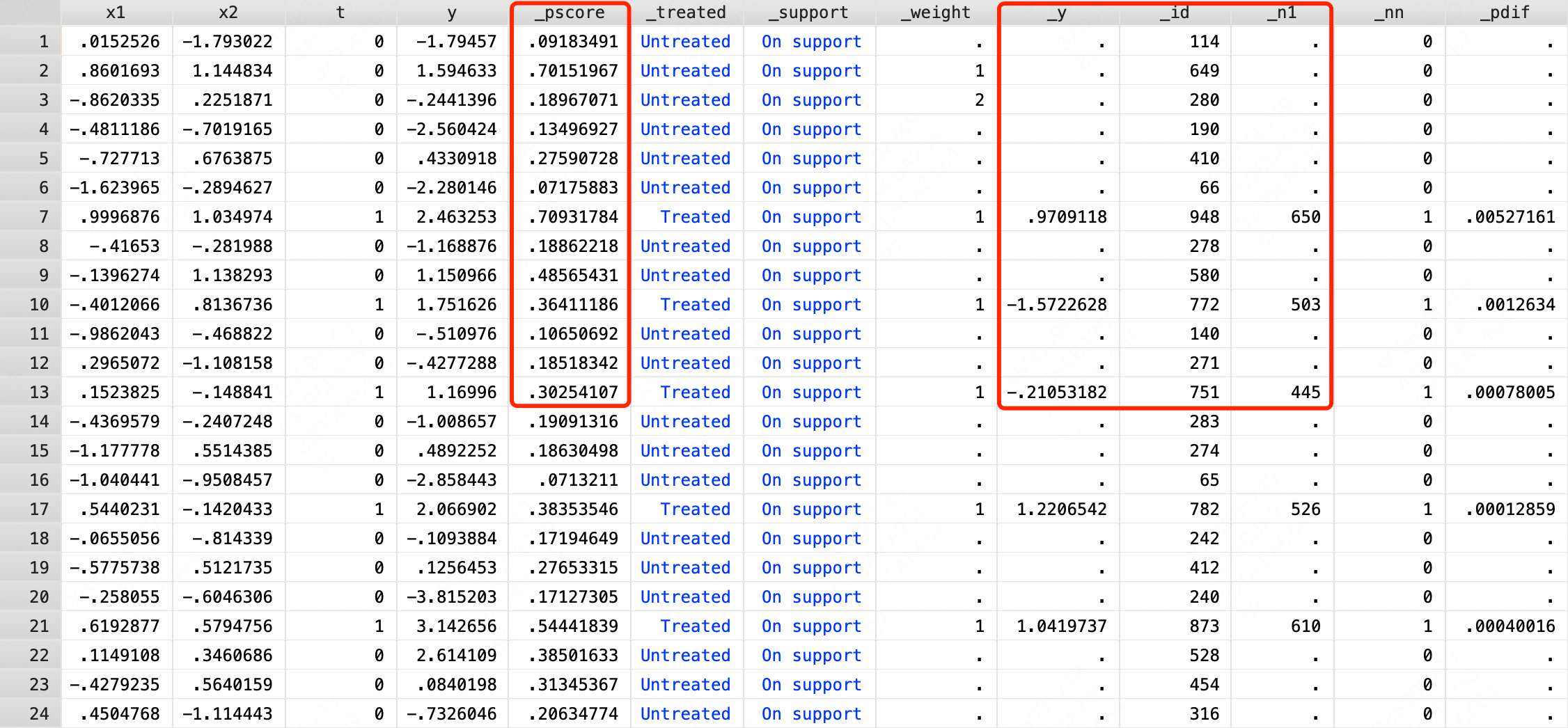
4.2.1 倾向得分
把第一行的数据拿出来手动计算一下倾向得分。
在逻辑回归模型中,针对任意样本,其分类结果为
1
1
1的概率为
f
=
1
1
+
e
−
y
^
f=\frac{1}{1+e^{-\hat{y}}}
f=1+e−y^1
其中,
y
^
=
w
1
∗
x
1
+
w
2
∗
x
2
+
.
.
.
+
w
n
∗
x
n
+
b
\hat{y}=w_1*x_1+w_2*x_2+...+w_n*x_n+b
y^=w1∗x1+w2∗x2+...+wn∗xn+b。
把第一行的数据和逻辑回归参数带入上式,得到
P
=
1
1
+
e
−
0.9068298
∗
0.0152526
+
0.8100408
∗
1.793022
+
0.8528442
=
0.09183491063414505
P=\frac{1}{1+e^{-0.9068298*0.0152526+0.8100408*1.793022+0.8528442}}=0.09183491063414505
P=1+e−0.9068298∗0.0152526+0.8100408∗1.793022+0.85284421=0.09183491063414505
显然,该值和Stata中计算的倾向得分值是一致的。
4.2.2 数据匹配
因为代码中使用的是最基础的近邻匹配,且仅匹配一个样本,所以匹配的过程没啥需要补充的,我们重点要分析的是匹配结果。
输入指令: pstest x1 x2, both graph,可以查看匹配前后协变量的差异。这里核心需要关注的是“%bias”列和“p>|t|”列,其含义分别是匹配前(U行)后(M行)协变量的差异的标准化后的百分数和差异是否显著(
<
0.05
<0.05
<0.05时显著)。
显然,对于
x
1
x_1
x1和
x
2
x_2
x2来说,均是匹配前有显著差异,匹配后无显著差异。
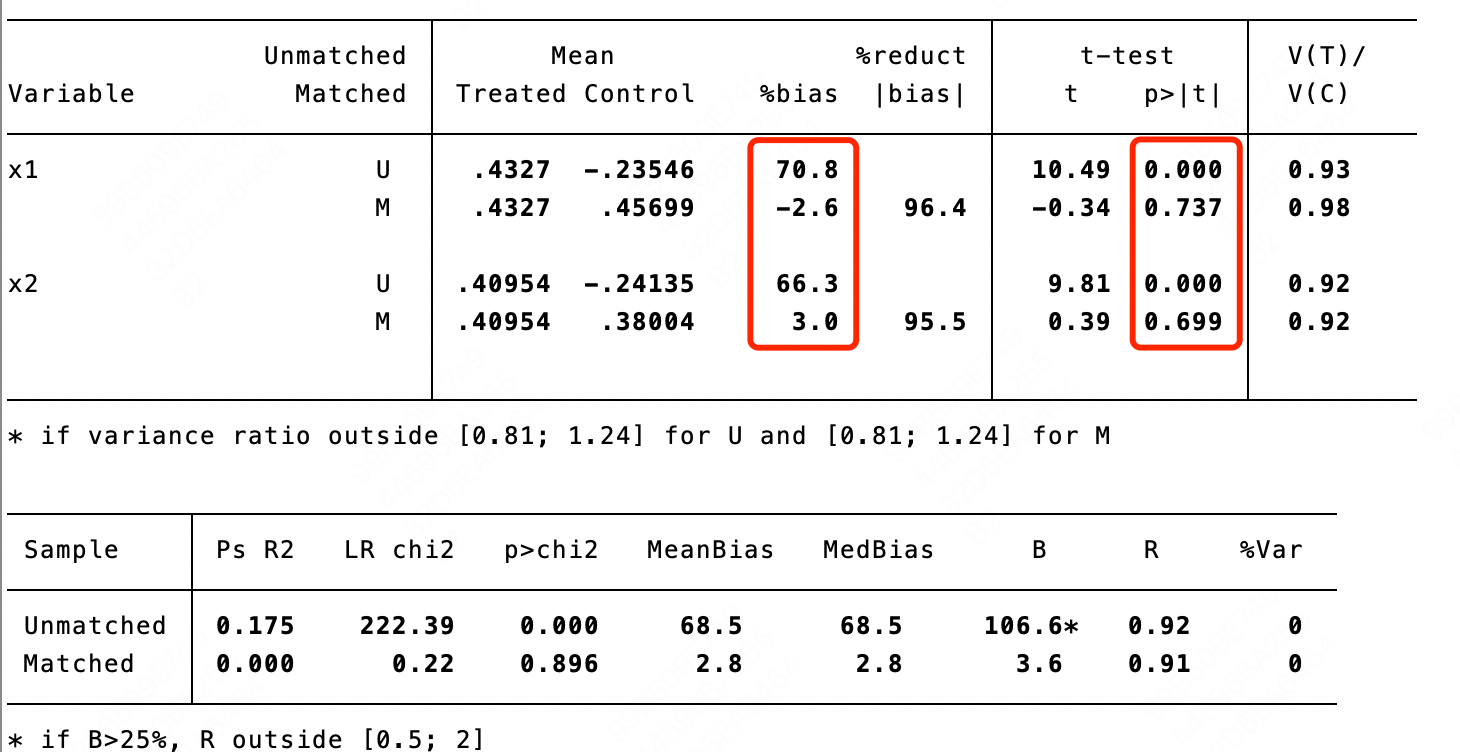
如果想在Stata中使用其他的匹配策略,可以参考下表,其中, k k k是要匹配的个体数, m m m是卡尺值。
| 匹配方法 | 含义 | Stata实现代码 |
|---|---|---|
| 近邻匹配 | 无策略变量组的样本中,倾向得分距离实验组样本最近的k个个体,作为对照组 | psmatch2 t x1 x2 y, outcome(y) n(k) |
| 带卡尺的近邻匹配 | 无策略变量组的样本中,在卡尺范围内的个体,倾向得分最近的k个,作为对照组 | psmatch2 t x1 x2, outcome(y) n(k) caliper(m) |
| 半径匹配 | 无策略变量组的样本中,卡尺范围内的所有个体,都作为对照组,求所有个体特征值的算数平均数 | psmatch2 t x1 x2, outcome(y) radius caliper(m) |
| 核匹配 | 无策略变量组的样本中,卡尺范围内的所有个体,都作为对照组,求所有个体特征值的加权平均数,加权依据是对照组和实验组倾向得分的差异值 | psmatch2 t x1 x2, outcome(y) kernel |
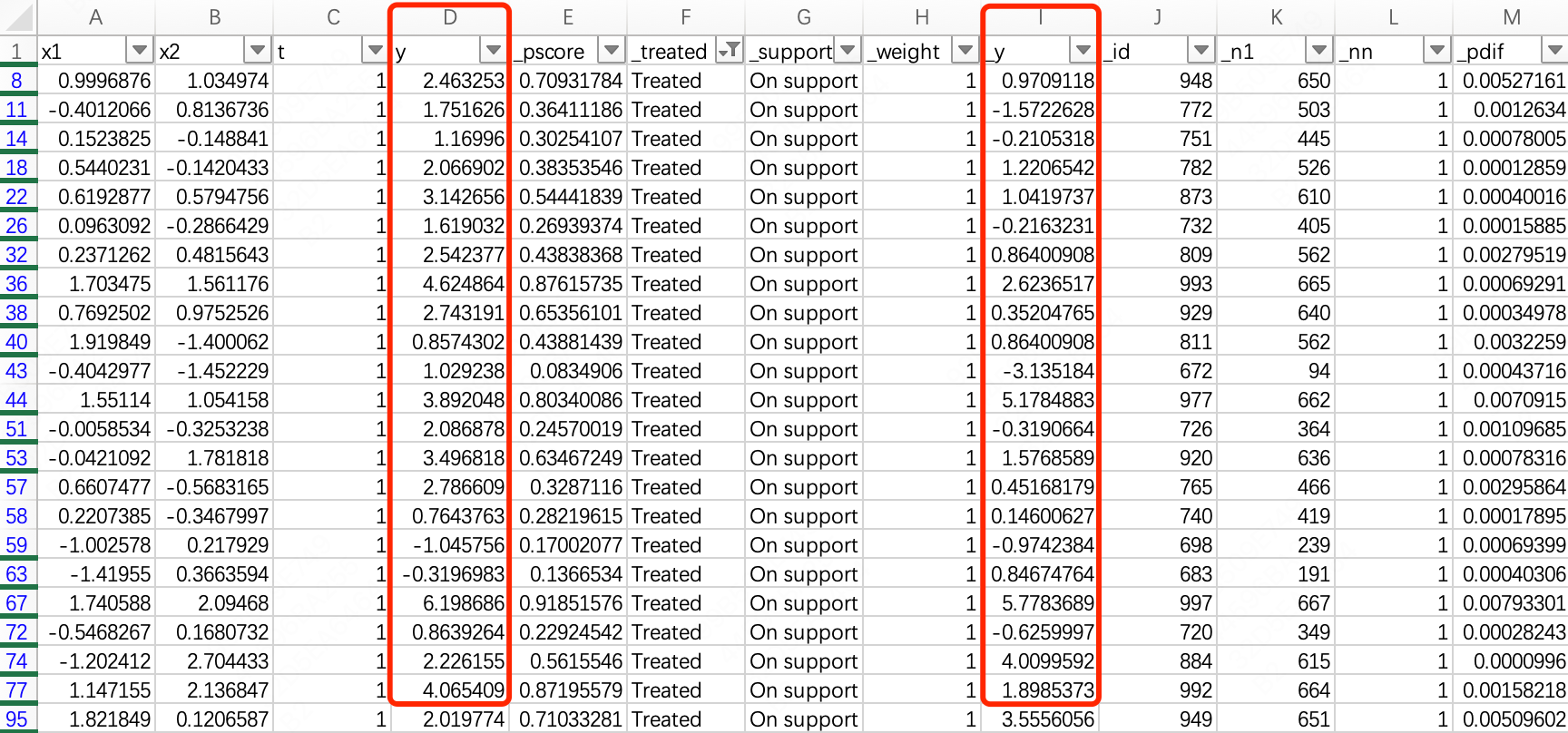
4.2.3 因果效应
把Stata中的数据拷贝到excel中,首先筛选出C列中标记为
1
1
1的所有数据,然后用D列的
y
y
y平均值减去I列的
_
y
\_y
_y平均值,即可得到实验组的因果效应值,为
0.9604
0.9604
0.9604,显然和Stata输出的结果也是相同的。
5 Python代码实现
作为一个算法同学,我使用Python的频率显著高于Stata,所以也需要知道如何在Python中实现PSM。
以下是具体的实现代码,主要包含以下5点内容:
(1) 获取数据样本。和Stata中使用的数据保持相同,协变量、策略变量和结果变量也都完全一致。
(2) 计算倾向得分。使用sklearn中的逻辑回归算法包实现。
(3) 根据倾向得分匹配样本。使用sklearn中的最近邻算法包实现。
(4) 计算因果效应值。根据匹配后的结果,直接计算结果变量的差值平均值作为 A T T ATT ATT。
(5) 评估因果效应值的准确性。使用评估DML算法时使用的AUUC指标进行评估。
import pandas as pd
from causalml.metrics import plot_gain, auuc_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import NearestNeighbors
if __name__ == '__main__':
data = pd.read_excel('psm_data.xlsx')
# 协变量和结果变量
features = ['x1', 'x2']
X = data[features]
y = data['t']
# 计算倾向得分
lr = LogisticRegression()
lr.fit(X, y)
data['propensity_score'] = lr.predict_proba(X)[:, 1]
print('coef_: {}, intercept_: {}'.format(lr.coef_, lr.intercept_))
# 使用最近邻方法进行匹配
treatment_data = data[data['t'] == 1]
control_data = data[data['t'] == 0]
nbrs = NearestNeighbors(n_neighbors=1).fit(control_data[['propensity_score']])
_, indices = nbrs.kneighbors(treatment_data[['propensity_score']])
control_matches = control_data.iloc[indices.flatten()]
matched_data = pd.concat([treatment_data.reset_index(), control_matches.reset_index()], axis=1)
matched_data.columns = ['treat_index', 'treat_x1', 'treat_x2', 'treat_t', 'treat_y', 'treat_propensity_score',
'control_index', 'control_x1', 'control_x2', 'control_t', 'control_y',
'control_propensity_score']
# 计算因果效应
matched_data['ATT'] = matched_data['treat_y'] - matched_data['control_y']
print('ATT = {}'.format(matched_data['ATT'].mean()))
# 计算AUUC值并绘制曲线
df = pd.DataFrame({
'y': pd.concat([matched_data['treat_y'], matched_data['control_y']]).reset_index(drop=True),
'x': pd.concat([matched_data['treat_t'], matched_data['control_t']]).reset_index(drop=True),
'psm': pd.concat([matched_data['ATT'], matched_data['ATT']]).reset_index(drop=True)
})
plot_gain(df, outcome_col='y', treatment_col='x', normalize=True, random_seed=10, n=100, figsize=(8, 8))
auuc = auuc_score(df, outcome_col='y', treatment_col='x', normalize=True, tmle=False)
print(auuc)
运行代码后,可以得到以下内容。对比Stata中的输出结果,无论是逻辑回归模型的参数还是 A T T ATT ATT值,都基本相同,即验证了代码的正确性。
coef_: [[0.89829989 0.80299241]], intercept_: [-0.85024718]
ATT = 0.991591266966967
psm 0.923152
Random 0.501969
dtype: float64
这里还有两点需要注意。
第一点是这段代码在得到匹配结果后就直接做差计算因果效应值了。更合理的方式可以是在匹配结果的基础上,再使用双重差分(DID)的逻辑计算因果效应值,也就是常见的PSM+DID组合。
第二点是我在这里使用了AUUC指标去评估PSM方法下因果效应值的有效性。从其他相关文档来看,几乎都没有使用AUUC指标,可能原因是PSM属于比较经典的方法,而AUUC是比较新的评估指标。但我是先学习的AUUC,再学习PSM,所以自然想用AUUC指标看看效果。
为了能获得 t = 0 t=0 t=0样本的因果效应值,我做了一个简单的假设:实验组样本和对应匹配样本的因果效应值相同,所以把他们组合到一起就可以计算AUUC了。如果想做的更细致些,可以先从实验组里给无策略变量组的每个样本做逐一匹配并计算因果效应值,然后再合并实验组样本。
不过,从已有的结果看,相比Random的 0.5 0.5 0.5,PSM的AUUC值达到了 0.92 0.92 0.92,已经证明了PSM方法下所得因果效应值的有效性。
6 总结
文章正文到此就结束了,本节总结一下三个比较重要的内容:
(1) 只要倾向得分相同,就可以去除选择偏差。
(2) 基于PSM的因果推断三个步骤:1-计算倾向得分;2-匹配样本;3-计算因果效应值。
(3) Stata和Python均可以实现基于PSM的因果推断。
7 相关阅读
PSM原理:https://academic.oup.com/biomet/article/70/1/41/240879?login=false
PSM学习视频:https://www.bilibili.com/video/BV168411W77c/?spm_id_from=333.788&vd_source=f416a5e7c4817e8efccf51f2c8a2c704
迭代期望定律:https://zhuanlan.zhihu.com/p/683927761#:~:text=%E8%BF%AD%E4%BB%A3%E6%9C%9F%E6%9C%9B%E5%AE%9A%E5%BE%8B%EF%BC%88l
DML文章:https://mp.weixin.qq.com/s?__biz=MzIyMzc3MjIyMw==&mid=2247485145&idx=1&sn=45257035c6431fb3eb7212a00d71048e&chksm=e8186d89df6fe49f897278bef5790de850b5c60402096700619c38894f92510cf3c6ed07d871&token=1313390928&lang=zh_CN#rd
潜在结果框架:https://mp.weixin.qq.com/s?__biz=MzIyMzc3MjIyMw==&mid=2247485117&idx=1&sn=65f5a43a00823ea564b6bea6f5eb4356&chksm=e8186deddf6fe4fbc0208208e93892f2f97bc9c0f0922537d89a3de925371241759a16262d0c&token=1685512830&lang=zh_CN#rd
逻辑回归模型:https://mp.weixin.qq.com/s?__biz=MzIyMzc3MjIyMw==&mid=2247484419&idx=1&sn=b03b5bdcb0af1acc0495e1ecb4ed0071&chksm=e8186f53df6fe645f06e4cebc89f46294dbcab8eaf2f105a36efff68bec0ff1d40197b3255ce&token=1544361017&lang=zh_CN#rd
























 2492
2492

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








