贝叶斯线性回归和多元线性回归构建工资预测模型

于 2022-12-05 16:55:35 发布
阅读量853 收藏 7
点赞数
文章标签： 线性回归 r语言 算法 回归 开发语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/tecdat/article/details/128196009
版权
本文介绍了如何使用贝叶斯线性回归和多元线性回归来构建工资预测模型，探讨了在劳动经济学领域的工资研究。通过R语言分析横断面数据，包括探索性数据分析、简单的线性回归、变量转换、贝叶斯模型平均和预测。重点讨论了教育程度和工作小时数对工资的影响，并展示了如何通过贝叶斯方法进行模型选择和预测。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

原文链接：http://tecdat.cn/?p=21641

在劳动经济学领域，收入和工资的研究为从性别歧视到高等教育等问题提供了见解（点击文末“阅读原文”获取完整代码数据）。

工资模型

在本文中，我们将分析横断面工资数据，以期在实践中使用贝叶斯方法，如BIC和贝叶斯模型来构建工资的预测模型。

相关视频

加载包

在本实验中，我们将使用dplyr包探索数据，并使用ggplot2包进行数据可视化。我们也可以在其中一个练习中使用MASS包来实现逐步线性回归。

我们将在实验室稍后使用此软件包中使用BAS.LM来实现贝叶斯模型。

数据

本实验室将使用的数据是在全国935名受访者中随机抽取的。

这是观察研究还是实验？

  • 观察研究

探索数据

与任何新数据集一样，标准的探索性数据分析是一个好的开始。我们将从工资变量开始，因为它是我们模型中的因变量。

  • 关于工资问题，下列哪种说法是错误的？

  • 7名受访者每周收入低于300元

summary(wage)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   115.0   669.0   905.0   957.9  1160.0  3078.0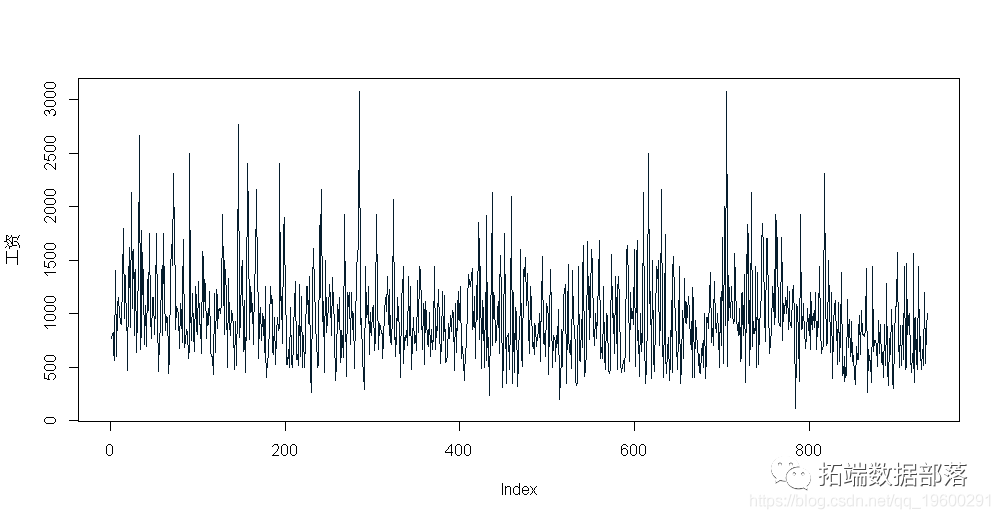

83a78ebbb701413d5ed08e56e697204f.png

61cc214624bd6fd1289c1972e1a22401.png

由于工资是我们的因变量，我们想探讨其他变量之间的关系作为预测。
练习：排除工资和工龄，选择另外两个你认为可以很好预测工资的变量。使用适当的图来形象化他们与工资的关系。

点击标题查阅往期内容

08a36555ce57b2251cffffe37513da93.jpeg

视频：R语言中的Stan概率编程MCMC采样的贝叶斯模型

outside_default.png

左右滑动查看更多

outside_default.png

01

b341819ef649edf1fe006b8aa344a397.png

02

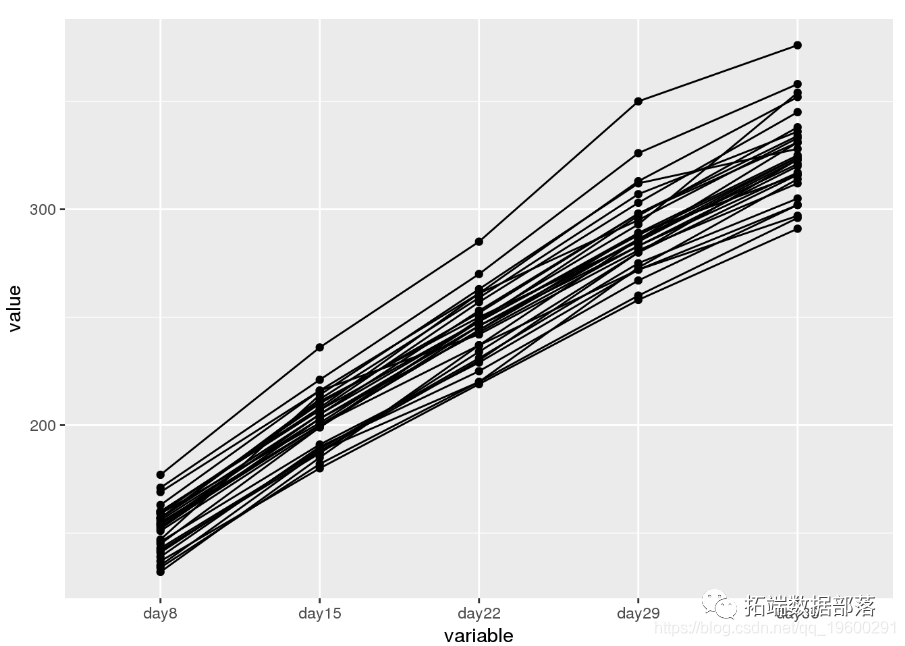
6414833e28c0b076ed84eda7f88be4d8.png

03

ef3bfd1271aa5650bc64086de009475b.png

04

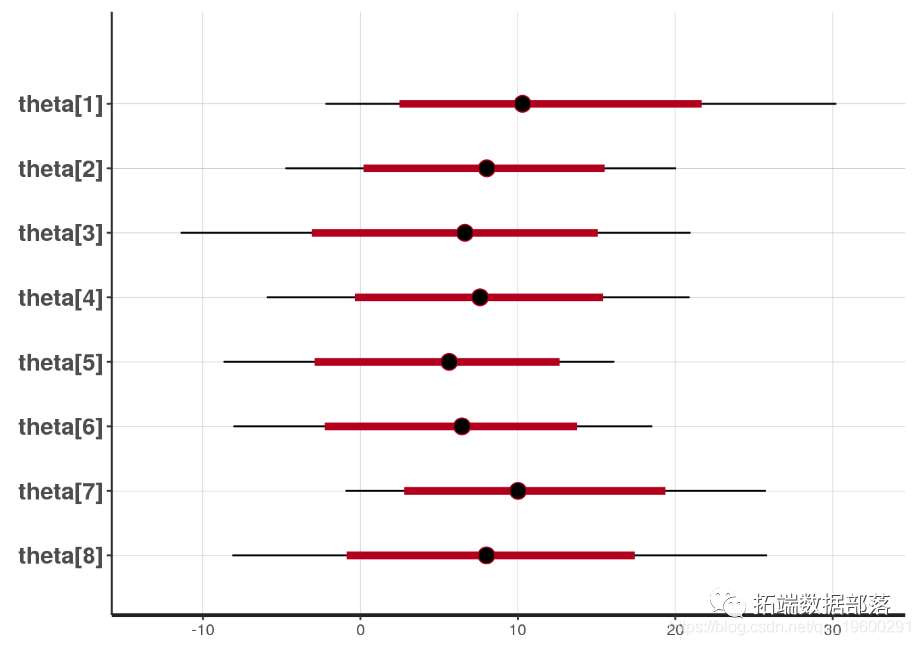
434638d340bfe3c110cffb6346afd884.png


受教育程度和工作小时数似乎是工人工资的良好预测因素。

ggplot(data = wage, aes(y=wage, x=exper))+geom_point()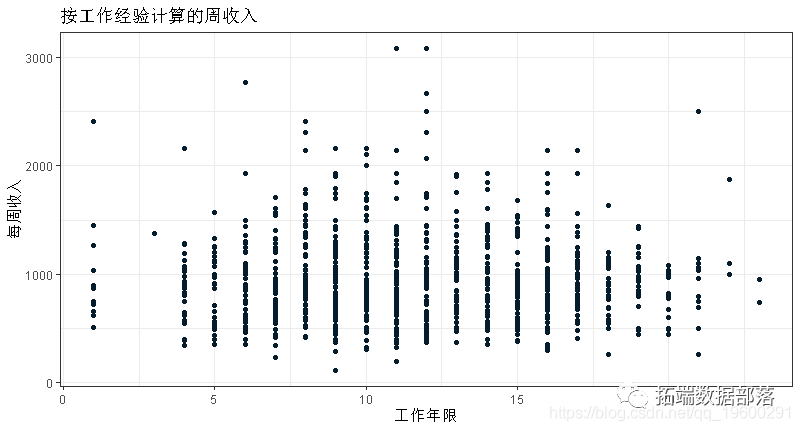

3523cccce40704eb16a45089c8ba1646.png

ggplot(data = wage, aes(y=wage, x=educ))+geom_point()

7bf52f33e5e629d8caf9acbc78e9fdf5.png

简单的线性回归

对于我们在数据中看到的工资差异，一个可能的解释是，更聪明的人赚更多的钱。下图显示了周工资和智商得分之间的散点图。

ggplot(data = wage, aes(x = iq, y = wage)) +
  geom_point()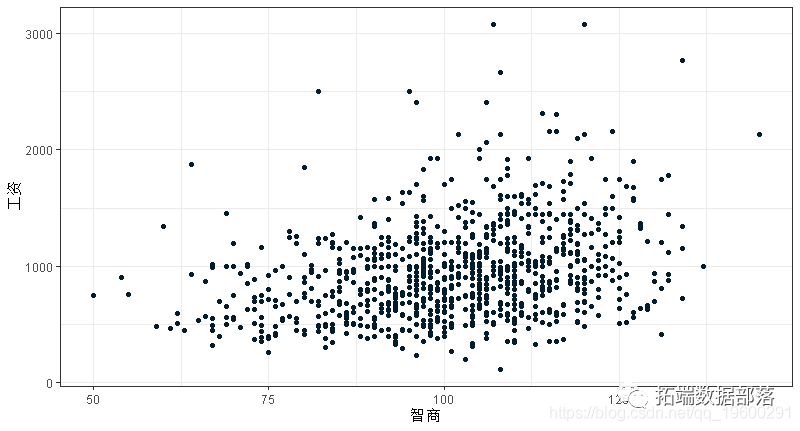

1688d7deb2c51488cbb8b89c1563760a.png

这个图是相当杂乱的。虽然智商分数和工资之间可能存在轻微的正线性关系，但智商充其量只是一个粗略的工资预测指标。我们可以通过拟合一个简单的线性回归来量化这一点。

m\_wage\_iq$coefficients
## (Intercept)          iq 
##  116.991565    8.303064
## \[1\] 384.7667

回想一下，在模型下

9013231db4cb830a5601b67b2ee7357e.png

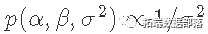如果使用 6e699982e633d7ba5530623899f80243.png 和参考先验 efcb49debb5590f85d905b33126c0a05.png   ，然后贝叶斯后验均值和标准差分别等于频数估计和标准差。

贝叶斯模型规范假设误差正态分布且方差为常数。与频率法一样，我们通过检查模型的残差分布来检验这一假设。如果残差是高度非正态或偏态的，则违反了假设，任何随后的推断都是无效的。

  • 检验m\_wage\_iq的残差。正态分布误差的假设有效吗?

  • 不，因为模型的残差分布是右偏的。

qqnorm(m\_wage\_iq$residuals)
qqline(m\_wage\_iq$residuals)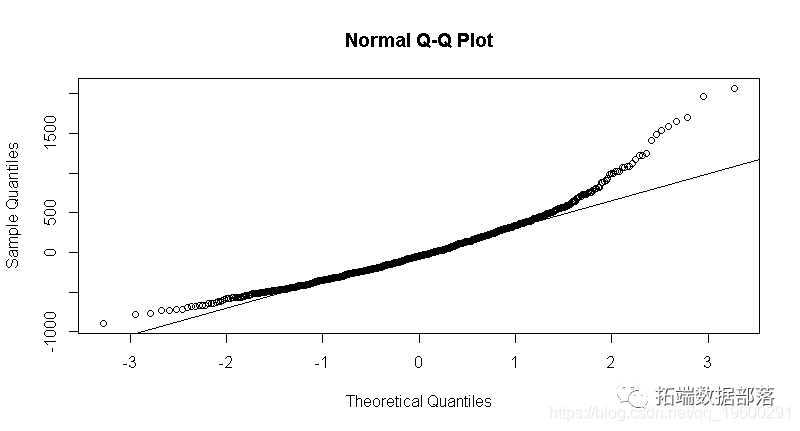

8d3df5646e549c2d18ab6f1af2c388cc.png

6e7253763bce05e8f1065a6828557900.png

练习：重新调整模型，这次使用educ（教育）作为自变量。你对上一个练习的回答有变化吗？

## (Intercept)        educ 
##   146.95244    60.21428
summary(m\_wage\_educ)$sigma
## \[1\] 382.3203

4bfea26e310e647936d02cb54c2ca6cf.png

69d009386c17e0a2229033ecf0f65db8.png

同样的结论是，该线性模型的残差与ϵi∼N（0，σ2）近似正态分布&#

最低0.47元/天 解锁文章
博客
2024年B2B外贸企业出海白皮书|附200+份报告PDF汇总下载
06-10 44
无论是东南亚市场的深度耕耘，还是跨境支付的技术赋能，其核心均指向对“效率”与“信任”的重构——这既是应对当下挑战的密钥，亦是赢得长期竞争的底层逻辑。B2B跨境电商凭借76%的物流占比，成为供应链整合的核心力量，电子家电、玩具母婴、纺织等品类占货物贸易出口前三，分别达18%、17%、17%。广东以23%的企业占比位居首位，浙江、江苏、上海紧随其后，构成沿海核心带。未来拓展中，美国（11%）、日韩（10%）、新加坡（8%）等市场与越南（8%）等新兴市场形成“双轨驱动”，反映企业对风险分散与利润增长的平衡考量。
博客
Python多层LSTM优化Seq2Seq序列模型预测社交网站用户签到时空轨迹数据
06-10 507
通过均方根误差（RMSE）和决定系数（R²）评估模型表现：Seq2Seq模型的RMSE最低（0.086），R²达0.354，显著优于LSTM（RMSE=0.104，R²=0.228）和Transformer（RMSE=0.113，R²=-0.208）。清洗后的数据保存为CSV格式，并通过散点图可视化对比：原始数据分布松散且包含大量离群点（图1），清洗后的数据则集中于目标区域，有效提升后续建模的可靠性（图2）。实践表明，Seq2Seq模型在数据稀疏场景下仍能保持稳定性能，尤其适用于签到频率中等的用户群体。
博客
PySpark、Plotly全球重大地震数据挖掘交互式分析及动态可视化研究
06-05 807
Yapeng Zhao 是一名具备专业素养的数据分析师，在数据处理与分析领域积累了扎实的技术能力，其在大数据框架应用、多维数据可视化及分布式计算优化方面的实践经验，为本研究的数据处理效率提升与分析模型构建提供了重要技术支持。项目以1965-2016年全球重大地震数据集（Global Major Earthquake Dataset）为研究对象，综合运用PySpark分布式计算框架、高德地图逆地理编码服务及Plotly动态图表工具，系统性挖掘地震活动的时空规律与能量特征。中国西部因板块构造活动成为地震热点；
博客
2025中国零售渠道演变趋势报告130+份汇总解读|附PDF下载
06-04 204
图注：左图为大卖场面积缩小至标超的TOP5省份占比（山西31%、天津29%、陕西26%、河南19%、广西12%），右图为停售成衣家电的TOP5省份占比（贵州55%、湖南35%、河南34%、山西31%、重庆20%），数据来源：尼尔森IQ零售核查。：会员店以“高质选品+场景体验”构建壁垒，山姆会员店新增“健康监测体验区”，带动保健品销售增长28%；：内容电商（+31%）、折扣电商（+35%）、会员店（+25%）成为增长三驾马车，而大卖场（-10%）、母婴店（-11%）等传统业态面临结构性调整压力。
博客
视频讲解|Python图神经网络GNN原理与应用探索交通数据预测
06-03 664
全文链接 ：tecdat.cn/?p=42421分析师： JiQuan Zhao，Jiaqi Teng在数据科学的浩瀚宇宙中，我们如同孜孜不倦的探索者，不断追寻着更高效、精准的数据分析方法。从数据科学家的视角看，数据不仅是一串串数字，更是蕴含着巨大价值的宝藏，等待我们用合适的工具去挖掘（点击文末“阅读原文”获取完整智能体、代码、数据、文档）。近年来，非欧式空间数据大量涌现，传统神经网络在处理这类数据时力不从心。图神经网络（GNN）凭借其独特的设计，如邻居节点聚合、消息传递机制等，成为处理非欧式数据的有力武器
博客
2025中国企业研发数字化转型白皮书200+份汇总解读|附PDF下载
06-03 39
原文链接：tecdat.cn/?p=42414当前，数字化浪潮正重塑企业研发体系。随着云计算、AI与大数据技术的深度渗透，研发管理从传统流程驱动向数据智能驱动跃迁（点击文末“阅读原文”获取专题报告合集PDF版本）。本报告汇总解读首先勾勒行业全景，揭示硬件与软件研发管理工具的市场分野；其次聚焦SaaS赛道，解析头部企业竞争逻辑；最后结合技术趋势与企业实践，提炼适配不同场景的转型方法论。值得关注的是，报告中所有数据均来源于公开行业调研与专家访谈，力求以客观视角呈现行业真实生态。本报告汇总解读聚焦中国企业研发数字
博客
2025中国汽车全球化战略白皮书450+份汇总解读|附PDF下载
05-30 113
出口结构呈现显著转型特征：燃油车占比从2023年的59%微降至2024年的59%，纯电动车占比从30%提升至35%，插电混动与非插电混动分别从3%、2%增至5%、5%，电动化车型成为增长新引擎。报告内容涵盖欧洲、东南亚、拉美、中东、中亚等核心市场的政策环境、竞争格局及本地化策略，解析电动化、智能化浪潮下中国车企的机遇与挑战，并结合典型企业的出海实践，提炼可复制的成功经验。营销层面，借势欧洲杯、南美杯等体育IP提升曝光，如比亚迪赞助2024年欧洲杯，品牌搜索量增长300%；
博客
视频讲解|Stata和R语言自助法Bootstrap原理结合GARCH对sp500收益率数据分析
05-30 863
该实现基于 Palm (1996) 的测试，该测试通过重新分类标准化残差而不是根据它们的值（如在标准测试中），而是根据它们的大小，计算在存在非独立同分布观察的情况下的测试，计算观察到小于标准化残差的值的概率，该残差应该是相同的标准均匀分布。例如，在研究人们查看Facebook个人资料的平均时间时（如视频所示，数据呈现右偏态，且仅有21个观测值，使用传统t程序存在顾虑），自助法通过对这21个观测值进行有放回的重抽样，来模拟从总体中抽取多个样本的过程，进而估计平均时间这一统计量的分布情况。
博客
2025人形机器人行业趋势报告110+份汇总解读|附PDF下载
05-29 237
本报告汇总解读聚焦人形机器人行业前沿动态，以数据驱动的专业分析框架，整合多份权威行业研究成果，深度解析技术演进、市场格局与产业机遇。：中国脑卒中患者2876万，康复治疗率不足40%，傅利叶智能上肢康复机器人已使30%患者手部功能恢复，市场规模年增55%。：依托汽车供应链优势，2024年Q4部署1000台工厂机器人，目标售价2万美元，单台年替代工时达2000小时。：普渡机器人全球市占率23%，其送餐机器人在全球5000家餐厅部署，单台日均服务150桌，故障率<0.3%。
博客
2025企业数字与人工智能AI就绪度报告570+份汇总解读|附PDF下载
05-29 225
本报告汇总解读基于《Thoughtworks：2025企业数字与人工智能就绪度报告》及文末570+份人工智能行业研究报告的数据，以数据驱动的专业分析框架，深度解析企业在数字与人工智能领域的就绪度现状与提升路径（2024年中国AI大模型产业发展与应用研究报告 报告2025-01-22AI时代的抉择-以“信”筑基-行稳“智”远 报告2025-01-21。报告通过对全球1000家企业的调研数据，揭示了技术战略、持续改进与投资回报之间的深层关联，为企业勾勒出从战略制定到执行落地的完整图谱。
博客
消费者网络购物意向分析：调优逻辑回归LR与决策树模型在电商用户购买预测中的应用及特征重要性优化
05-29 1018
通过相关性分析和VIF值计算，删除“管理页面数”“信息页面数”“产品相关页面数”“退出率”等相关性较高的特征，保留“管理页面停留时长”“信息页面停留时长”“产品相关页面停留时长”“跳出率”“页面价值”“特殊日期”“月份”“访客类型”等特征。目标变量“是否购买”的类别分布显示，购买人数占比13.9%，未购买人数占比86.1%，类别分布不均衡。对未购买的预测效果良好（精确率92%、召回率94%、F1分数93%），但对购买的预测效果较差（精确率59%、召回率53%、F1分数56%），漏判和误判情况较为严重。
博客
Python农产品产量预测数据分析：神经网络、PCA、随机森林、模型融合建模实践
05-26 1004
文中通过Python编程语言，综合运用Pandas、Matplotlib、Seaborn等工具，结合决策树（Decision Tree）、随机森林（Random Forest）、主成分分析（PCA）等算法，系统解析环境变量与产量的关联机制，并创新性提出"数据预处理-特征工程-多模型对比"的农业数据分析范式。对"作物病害状态"（crop_disease_status）字段进行缺失值处理与序数编码，将病害程度转化为数值型变量（无病害=0，轻度=1，中度=2，重度=3）。
博客
Python用Transformer、Prophet、RNN、LSTM、SARIMAX时间序列预测分析用电量、销售、交通事故数据
05-22 933
在数据驱动决策的时代，时间序列预测作为揭示数据时序规律的核心技术，已成为各行业解决预测需求的关键工具。本文基于某咨询项目的实际需求，通过对比分析五种主流预测模型（SARIMAX、RNN、LSTM、Prophet、Transformer）在多类数据集上的表现，探讨模型选择逻辑与参数调优策略，为行业应用提供可落地的解决方案。本研究通过多场景实证分析，揭示了时间序列预测模型的“数据-模型适配法则”：没有最优模型，只有最适合特定数据特征的方案。能源消耗数据的ADF检验p值>0.05，表明非平稳，需差分处理；
博客
2025人工智能AI创新中的可观测性研究报告550+份汇总解读|附PDF下载
05-22 99
然而，随着人工智能代理能力的不断增强，其潜在的风险也不容忽视。北美地区以88%的可观测性项目成熟度领先欧洲（47%），这种差异既源于技术投入的梯度，也与监管环境、数据战略密切相关——尽管欧盟推出AI法案，但北美企业更注重模型准确性（51% vs 欧洲32%）与合规落地的量化指标。报告显示，企业在数据质量、数据管道、AI/ML模型三大核心领域的可观测性投入呈现显著分化：76%的受访者已优化或实施数据质量与管道监控项目，而模型可观测性的“优化级”占比仅23%，凸显模型全生命周期管理的技术门槛。
博客
MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例
05-21 659
本方案已在某航空制造企业的发动机生产线部署，通过实时采集传感器数据并输入训练好的模型，可提前7天预测设备剩余寿命，将非计划停机时间减少35%，维护成本降低28%。结果显示，预测曲线与真实曲线在趋势与关键拐点上高度吻合，尤其在设备临近失效阶段（剩余寿命低于50时），模型能准确捕捉退化加速特征，为维护决策提供了可靠依据。其中，( N ) 为样本总数，( Y_i(t) ) 为第( i )个样本的真实剩余寿命序列，( \hat{Y}_i(t) ) 为预测序列。归一化可确保不同量纲的特征在模型训练中具有同等权重。
博客
Python谷歌商店APP评分预测：LASSO、多元线性回归、岭回归模型对比研究
05-20 911
在模型构建阶段，我们对比多元线性回归（MLR）、LASSO 回归、岭回归三种经典算法，通过严谨的模型评估指标 —— 均方误差（MSE）与决定系数（R2R2 Score），量化不同模型在 APP 评分预测中的表现差异。目前，完整的《谷歌商店 APP 评分预测项目文件》已上传至会员社群，扫码进群即可与 600 + 行业精英共同探讨技术细节，获取代码、数据集及可视化报告，一同解锁数据驱动的 APP 增长新策略。可以转换为int型。由输出结果可见，最少的评论是0条，最多的评论是7千多万条，平均数是40多万条。
博客
2025年医美行业报告60+份汇总解读|附PDF下载
05-20 227
本报告通过梳理政策监管、消费行为、机构竞争等维度，提炼关键数据指标，如华东地区居民人均可支配收入与医美机构数量的关联性、针剂正品率分布等，旨在帮助读者系统把握行业脉络，预判趋势并制定战略。报告结构上，先以 “市场全景” 勾勒行业轮廓，再以 “消费洞察” 解析需求端特征，继而从 “供给变革” 探讨机构与技术升级，最后以 “未来展望” 提出合规化与数字化解决方案。蛋壳研究院：医美能量源设备白皮书 报告2023-02-09 医疗美容行业白皮书：Z世代崛起、轻医美主导，行业正在换打法 报告2025-05-19。
博客
Python+AI提示词糖尿病预测融合模型：伯努利朴素贝叶斯、逻辑回归、决策树、随机森林、支持向量机SVM应用
05-16 1106
其中，(w_i)为特征权重，反映症状对患病风险的影响程度。原始SVM模型（线性核）准确率仅68%，经网格搜索优化（AI提示词：用RBF核和网格搜索提升SVM在医疗数据中的分类性能），选定C=100、gamma=0.1，准确率提升至97%，表明非线性核函数能有效挖掘特征间复杂关联（图10、图11）。研究团队基于真实医疗数据集，系统对比了逻辑回归（LR）、决策树（DT）、随机森林（RF）、支持向量机（SVM）和伯努利朴素贝叶斯（BNB）等算法的表现，并通过模型融合技术实现预测性能的跨越式提升。
博客
2025年全球人工智能AI信任、态度与应用研究报告530+份汇总解读|附PDF下载
05-15 355
数据显示，新兴经济体在AI使用率与信任度上显著领先：印度、尼日利亚等国的AI使用率超90%，而荷兰、日本等发达经济体仅为43%-50%。在工作场景中，58%员工定期使用AI工具，其中73%采用公共生成式AI（如ChatGPT），但仅40%企业制定了生成式AI使用政策。值得关注的是，尽管发达经济体对AI技术能力的信任度达65%，但对其安全与伦理的信任仅52%，反映出技术乐观与社会风险的认知割裂。然而，仅49%教育机构提供AI使用政策指导，20%明确禁止生成式AI，导致59%学生存在违规使用行为。
博客
Python与MySQL网站排名数据分析及多层感知机MLP、机器学习优化策略和地理可视化应用|附AI智能体数据代码
05-15 663
值得关注的是，项目中开发的「数据清洗-特征工程-模型训练-可视化反馈」闭环框架，已在实际应用中帮助客户提升关键词排名30%以上，验证了技术方案的有效性。通过关联分析热力图（图4）发现：「页面加载速度」与「移动端适配性」呈强正相关（相关系数0.82），而「关键词密度」与「用户跳出率」呈负相关（-0.65）。使用K-means算法，将网站分为「高流量高转化」「低流量高粘性」等4类，为差异化优化提供依据（AI提示词：利用K-means聚类分析网站流量特征，划分用户群体）。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值