CS61A fa2021 Composing Programs 2.8 Efficiency 效率

最新推荐文章于 2023-04-10 16:21:02 发布

theWooding

最新推荐文章于 2023-04-10 16:21:02 发布

阅读量497

点赞数

分类专栏： Composing Programs 第二章文章标签：开发语言 python

本文链接：https://blog.csdn.net/theWooding/article/details/126273532

版权

Composing Programs 第二章专栏收录该内容

12 篇文章 0 订阅

订阅专栏

如何抽象和处理数据，答案往往不是唯一的。我们倾向于在众多答案中选择最有效率的一个。效率取决于我们抽象今和处理数据所使用的计算机资源，例如完成一个函数计算或者声明一个实例需要花多少时间，多少内存等。在代码上下功夫可以极大的改变程序运行的效率。

2.8.1 效率度量（Measuring Efficiency）

一个程序运行起来耗时多长？占用多少内存？这样的问题想要得到一个标准化答案是十分困难的。因为它的结果受制于许多关于计算机配置的细节。不过我们可以退而求其次，不求具体的计算机资源，而是用某些操作，例如函数调用，进行的次数来描述程序的效率。

拿我们的老朋友，斐波那契数列来说吧。

>>> def fib(n):
        if n == 0:
            return 0
        if n == 1:
            return 1
        return fib(n-2) + fib(n-1)
>>> fib(5)
5

我们把程序的计算过程罗列在下方，为了计算fib(5)，我们需要计算fib(3)和fib(4)。而为了计算fib(3)，我们又得计算fib(1)和fib(2)。计算过程如树一般，每一个蓝点都表示为一次完整而又复杂的斐波那契数列计算。

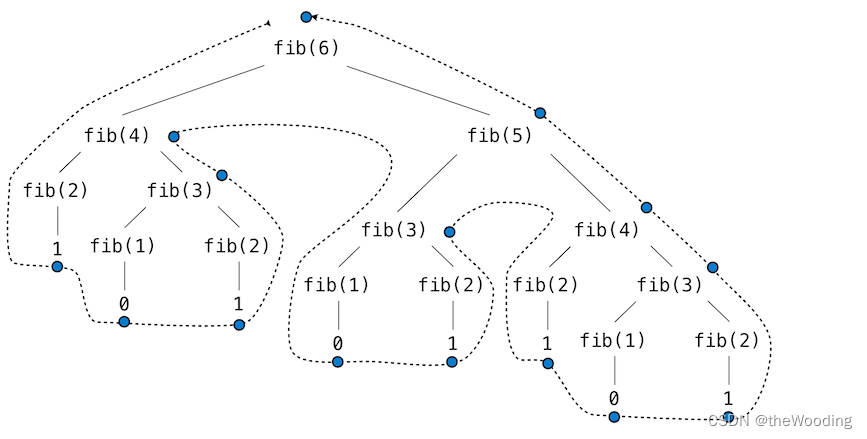
这个函数十分完美地给我们展现了递归的基本思想，具有教育意义。但是对于计算一个斐波那契数列而言，那就太糟糕了。因为他做了太多的重复计算。

我们定义一个高阶函数count，以一个函数为参数，并具有一个变量call_count用来存放函数的调用次数。以此，我们来试试fib函数到底被调用了多少次。

>>> def count(f):
        def counted(*args):
            counted.call_count += 1
            return f(*args)
        counted.call_count = 0
        return counted

通过累计fib函数的调用次数，我们发现随着要求的斐波那契数的增长，调用次数也将爆炸性的增长。这就是树递归的特性之一。

>>> fib = count(fib)
>>> fib(19)
4181
>>> fib.call_count
13529

使用空间（Space）

在讨论一个函数的使用空间之前，必须先给大家讲一讲内存在我们的函数式编程中是如何被使用、暂存与归还的。在计算一个表示式时，编译器会保存当前环境的所有活跃的框架和所有活跃的值。任何具有正在求值的表达式的环境皆为活跃的环境。当函数调用后产生的首个框架返回值后，环境转为非活跃状态。

在计算斐波那契数时，编译器会按图片所示的顺序计算每个斐波那契数的值。在计算每个节点时，计算机都会记住上一个节点的值。已经计算完成的分支，将不再占用内存，因为它们不会影响下一步的计算。通常，树递归所需内存与树的深度成正相关。

下图展示出了在计算fib(2)时环境内的框架。在计算fib(2)时，至return语句后的表达式，先计算fib(n-2)即fib(0)，结果为0。一旦fib(1)计算结束，就不再保存为了求fib(1)而调用fib时所创建的框架了。他不再是当前环境的一部分。因此，我们认为只有能归还那些不再需要的部分所占用的内存，才能称得上是良好的编译器。而后，再求fib(n-1)，即fib(1)。此时再调用一次fib函数，因此又将有新的框架被创建。待fib(n-2)与fib(n-1)均计算完成后，fib(2)的函数框架又将活跃起来，将之前两个结果相加，返回最后的结果。

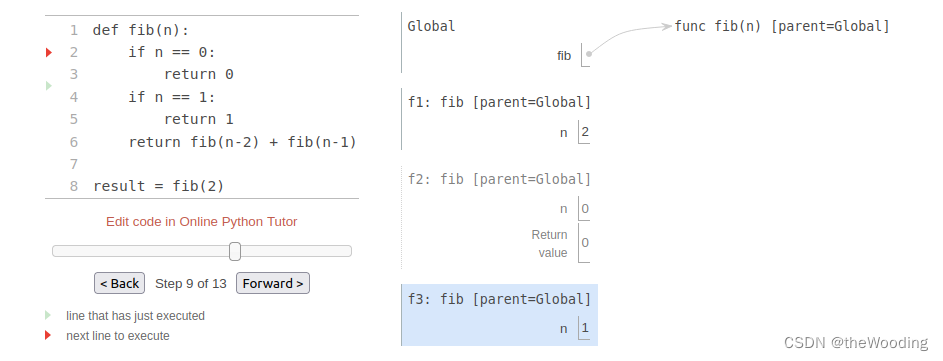
高阶函数count_frames用变量open_count来储存所有未返回的f函数所创建的框架数。max_count变量储存框架数的最高记录。

>>> def count_frames(f):
        def counted(*args):
            counted.open_count += 1
            counted.max_count = max(counted.max_count, counted.open_count)
            result = f(*args)
            counted.open_count -= 1
            return result
        counted.open_count = 0
        counted.max_count = 0
        return counted

>>> fib = count_frames(fib)
>>> fib(19)
4181
>>> fib.open_count
0
>>> fib.max_count
19
>>> fib(24)
46368
>>> fib.max_count
24

2.8.2 记忆化（Memoization）

记忆化能够改善一些递归函数重复计算的缺点，以此大大提高程序的效率。记忆化的函数在递归过程中，会记住对应的参数和计算结果。例如我们在斐波那契数列的递归过程中，第二次算到了fib(25)，便不会再去计算一次，而是沿用第一次计算fib(25)时得到的结果。

我们可以用高阶函数或者装饰器的手段来实现记忆化。下面定义的memo函数会把先前的计算结果暂存起来，并且可以通过对应的参数去检索他们。

>>> def memo(f):
        cache = {}
        def memoized(n):
            if n not in cache:
                cache[n] = f(n)
            return cache[n]
        return memoized

如果我们对fib函数调用memo，使fib函数记忆化，那么他的计算过程便会有些许变化。如下图所示。

在计算fib(5)时，我们需要计算fib(3)与fib(2)，这两个结果我们在fib(4)时已经计算过了，所以直接沿用已经保存的结果。记忆化让我们省了不少事。

再次使用count函数，我们发现计算记忆化的fib(19)时，fib函数的调用次数少了许多许多。

>>> counted_fib = count(fib)
>>> fib  = memo(counted_fib)
>>> fib(19)
4181
>>> counted_fib.call_count
20
>>> fib(34)
5702887
>>> counted_fib.call_count
35

2.8.3 增长量级（Orders of Growth）

从之前的例子我们可以发现，一个程序在运行时间与占用内存上可以具有很大的波动。但想要真正决定一个程序的运行时间与占用内存是一件十分困难的事，它们由诸多因素决定，但并非无路可循。我们可以把某些具有相同特点的程序集中起来分析。相同特点是什么？这里引入新的概念——增长量级。他指随着输入参数的增长，函数计算所消耗资源的增长情况。

为了了结增长极，我们下面引入一个函数count_factors，他用于计算能被形参n整除的整数个数。这个函数会尝试用n除于从0到n平方根之间的所有整数（包括平方根）。这个思路的原理在于如果存在整数k能被n整除，且k＜√n，则必定存在整数j=n/k，且j>√n。这种思路的极限情况就在√n上。

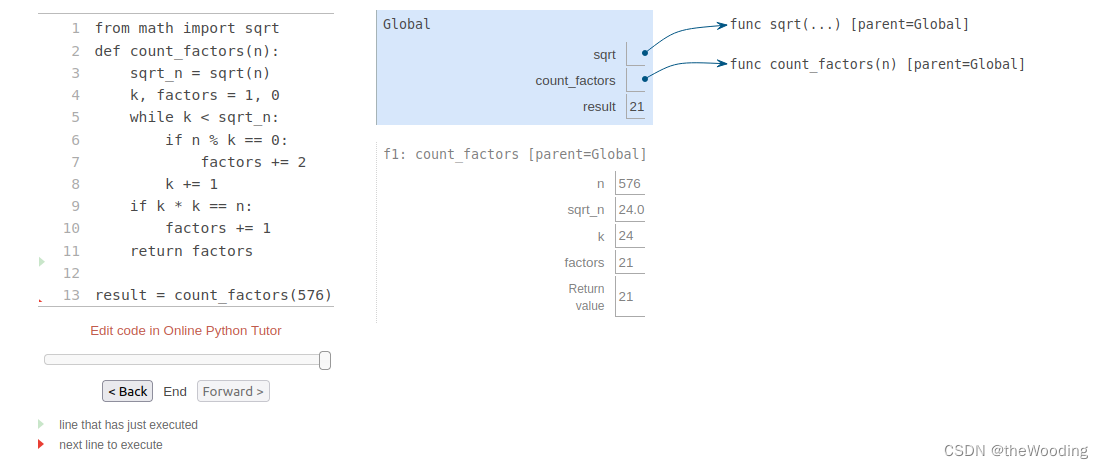
那么对于这个程序而言，怎么去测量他的运行时间呢？诚然，在不同的机器上会有不同的答案，所以很难得到一个标准答案。不如我们把目光放到计算步骤上？我们不难发现，执行while语句的次数等于小于√n的最大整数。在while语句段前后的语句，实际上都只执行过一次。我们设while语句内的语句数为w，while语句外的语句数为v，则总共执行的语句数为w⋅√n+v。虽然看起来可能有些理想化了，但这确实是衡量程序运行时间的一种手段。不过，常数w和常数v有时并无法代表问题的基本情况。在上述例子中，对变量factors的赋值语句有时执行，有时不执行。增长级解决了这个问题，与其考虑这些具体的细节，他在更概括性的层面上考虑问题。与其去定下一个确定的时间，不如去圈定一个时间范围。他认为计算count_factors(n)所需要的时间必定在某个范围之内，这个范围内的每个元素都是某个常数与√n的积。

θ符号(Theta Notation).

n是衡量输入参数尺寸的一个参数，并且这个尺寸有最小值m。R(n)是该参数下，计算机运行改程序所需的资源。在之间的例子中，n便是输入函数的参数本身，但情况并非都如此。如果我们的目的是计算一个数的平方根，那么用该数字的位数而不是数字本身来作为衡量输入参数的标准会更好。R(n)代表着程序需要的内存，或者要执行的简单步骤总数等等。在计算机中，固定的时间内只能执行固定数量的操作。因此，运行时间便与操作数成比例。若是存在与n(n>m)无关的常数k1与k2，使得：

$k_1\cdot f(n)\leqslant R(n) \leqslant k_2\cdot f(n)$

我们说R(n)的增长量级为Θ(f(n))，写作R(n)=Θ(f(n))。换句话说，不论多大的n， R(n)总是介于两个与f(n)成比例的值之间：

一个下限 k1⋅f(n) 与
一个上限 k2⋅f(n)

回到count_factors函数，我们仔细观察函数体就能发现，对于不同n的具体计算步骤数，他的增量级为Θ(√n)。

首先，如果k1 = 1，m = 0。所以count_factors函数的增量级下限为1⋅√n(n>0)。在while语句外有四行代。码，while语句体包括while语句自己共计两行代码，每一行代码都至少可以拆解为一个步骤。while语句体至少执行√n−1步。该程序合计至少需要计算4+3⋅(√n−1)步，大于增量下限1⋅√n。

然后，我们再证明存在一个上限。我们假设每行代码最多能包括p步计算，这是个理想性的假设。虽然这放到编程中不一定合适，但是放在我们这个问题中足够了。然后我们可以得到计算count_factors(n)最多需要p⋅(5+4√n)步。因为while循环内有4行代码，循环外有5行代码，假设每次布尔语境都能的到真值，便能得到上述结果。到此，令k2 = 5p，那么该程序执行的步数必将小于k2√n。

2.8.4 范例：求幂（Example: Exponentiation）

对给定的指数p与底数b，要求幂。递归是一种不错的方法

$\begin{align*} b^n &= b \cdot b^{n-1} \\ b^0 &= 1 \end{align*}$

把它写成函数如下：

>>> def exp(b, n):
        if n == 0:
            return 1
        return b * exp(b, n-1)

不难看出，这是个线性递归，且他的增量级为Θ(n)。和阶乘很像，我们可以很简单的将写递归写成迭代。

>>> def exp_iter(b, n):
        result = 1
        for _ in range(n):
            result = result * b
        return result

加上点小技巧——连续平方，可以大大减小求幂过程中的计算量。比如我们如果老老实实地计算 $b^8$ ：

$\begin{equation*} b \cdot (b \cdot (b \cdot (b \cdot (b \cdot (b \cdot (b \cdot b)))))) \end{equation*}$

不如把他拆成，三次平方计算。

$\begin{align*} b^2 &= b \cdot b \\ b^4 &= b^2 \cdot b^2 \\ b^8 &= b^4 \cdot b^4 \end{align*}$

这种方法在指数为偶数时能用，若指数为奇数，只需要拓展一下也不是难事：

$\begin{equation*} b^n = \begin{cases} (b^{\frac{1}{2} n})^2 & \text{if $n$ is even} \\ b \cdot b^{n-1} & \text{if $n$ is odd} \end{cases} \end{equation*}$

我们把它写成递归函数：

>>> def square(x):
        return x*x
>>> def fast_exp(b, n):
        if n == 0:
            return 1
        if n % 2 == 0:
            return square(fast_exp(b, n//2))
        else:
            return b * fast_exp(b, n-1)
>>> fast_exp(2, 100)
1267650600228229401496703205376

我们不难发现fast_exp函数的增长级为n的对数形式。正如我们发现计算 $b^{2n}$ 实际上只比计算 $b^n$ 多了一步，因此该对数的底为2，增长级为 $\Theta(\log n)$ （在算法中log或者lg默认底数为2）。当n越来越大时， $\Theta(\log n)$ 与 $\Theta(n)$ 的差距会变得十分惊人。当输入的指数n为1000时，fast_exp函数操作只有14步，但递归或者迭代函数exp却有1000步。

2.8.5 量级分类（Growth Categories）

增长量级用于方便度量程序的效率，或者比较不同的计算方法。许多不同的程序有着相同的增长量级。对于一个计算机科学家来说，了解各种增长量级以及区分程序的量级是一项基本技能。

常量级（Constants）.

$\Theta(n)$ 与 $\Theta(500 \cdot n)$ 是一个量级，这是Θ表达式的特性。说白了都是与n成正比。这是最基本也是最容易被人们忽略的一个量级。

对数量级（Logarithms）.

$\log_2 n$ 与 $\log_{10} n$ 时同一个量级的，对数的底并不影响量级本身。切换对数的底和切换常量级的常数一样。

嵌套（Nesting）.

若在外部计算中嵌套一个内部计算，那么整个程序的执行步数为内外步数的乘积（有些像复合函数的求导）。

举个例子，下面的overlap函数，它统计同时出现在列表a和列表b的元素数量。

>>> def overlap(a, b):
        count = 0
        for item in a:
            if item in b:
                count += 1
        return count
>>> overlap([1, 3, 2, 2, 5, 1], [5, 4, 2])
3

设列表b的长度为n，in操作符的增长量级为Θ(n)。而列表a的for循环增长量级为Θ(m)（m为列表a的长度）。这整个程序的增长级为Θ(m⋅n)。

低级项（Lower-order terms）.

在输入参数的增长过程中，计算流程中增长量级最大的一部分决定了整个程序对计算机资源的消耗。这也是增长量级的一个特点。在考量整程序时，舍弃除了最大量级的部分将不会影响最终的增长量级。

举例来说，下面的one_more函数统计列表a中加一后的结果也于列表a中的元素数量。在列表 [3, 14, 15, 9]中，14加一为15，也在原列表中，则返回1.

>>> def one_more(a):
        return overlap([x-1 for x in a], a)
>>> one_more([3, 14, 15, 9])
1

这儿的计算可以分为两部分，列表推导和调用overlap函数。对于一个长度为n的列表，列表推导的增长量级为Θ(n)，而overlap函数的增长量级为Θ( $n^2$ )。总量级为Θ( $n+n^2$ ) ，但这还不是最终结果。

Θ( $n^2+k\cdot n$ ) 和 Θ( $n^2$ ) 是一个量级，因为 $n^2$ 比任何常数k都具有决定性。为了简便，低级项在Θ表达式中总是被忽略。

常用量级（Common categories）.

按增长速度由慢至快，将一些常用的增长量级列在了下方。

当然存在其他量级，诸如count_factors函数的Θ(√n)。

指数量级比较独特，更改它的底数b也会影响它的量级。树递归的fib函数，他就是典型的指数量级。一般第n个斐波那契数可以通过下列公式近似计算：

$\LARGE \begin{equation*} \frac{\phi^{n-2}}{\sqrt{5}} \end{equation*}$

ϕ为黄金分割比：

$\large \begin{equation*} \phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180 \end{equation*}$

对增长量级的描述可以不限于输入，还可以用输出的结果来定义一个量级。所以以上树递归函数的增长量级就是 $\large \Theta(\phi^n)$ 。

theWooding

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
CS61A fa2021 Composing Programs 2.8 Efficiency 效率

CS61A fa2021 Composing Programs 2.8 Efficiency 效率
复制链接

扫一扫

专栏目录