CS61A fa2021 Composing Programs 2.9 Recursive Objects 递归对象

2.9   递归对象

若一个对象的某个属性值为所属同一个类的某个对象，则称其为递归对象。

问题：这个属性对象可以是自己吗？还是必须得是其他对象呢？

答：可以是自己，但这就是无限递归了。

2.9.1   链表（Linked List Class）

正如之间所介绍的，链表由两部分组成，第一部分是一个元素，第二部分是一个子链表。子链表又由两个部分组成……这就很有递归的味道了。直到empty，递归结束。

想讨论链表的递归，总得有链表供我们使用吧。链表满足序列的基本特性——有限长度与元素检索。下面我们通过代码来创建链表类与实现它的基本功能。

>>> class Link:
        """A linked list with a first element and the rest."""
        empty = ()
        def __init__(self, first, rest=empty):
            assert rest is Link.empty or isinstance(rest, Link)
            self.first = first
            self.rest = rest
        def __getitem__(self, i):
            if i == 0:
                return self.first
            else:
                return self.rest[i-1]
        def __len__(self):
            return 1 + len(self.rest)

>>> s = Link(3, Link(4, Link(5)))
>>> len(s)
3
>>> s[1]
4

链表类或许还不够完善，当创建完一个链表后我们只有检索单个元素的操作，却很难再整体观察该链表的每个元素。需要做一些改进，加一个新的方法。

>>> def link_expression(s):
        """Return a string that would evaluate to s."""
        if s.rest is Link.empty:
            rest = ''
        else:
            rest = ', ' + link_expression(s.rest)
        return 'Link({0}{1})'.format(s.first, rest)

>>> link_expression(s)
'Link(3, Link(4, Link(5)))'

这是个好函数，方便实用。如果把它与Link类的__repr__方法绑定起来就更方便啦。

>>> Link.__repr__ = link_expression
>>> s
Link(3, Link(4, Link(5)))

到此我们就基本 完成了Link类的实现。

一个函数里面可以定义另一个函数（闭包），列表里面可以有列表。链表也具有闭包的特性，即链表的第一个元素可以也是链表。

>>> s_first = Link(s, Link(6))
>>> s_first
Link(Link(3, Link(4, Link(5))), Link(6))

>>> len(s_first)
2
>>> len(s_first[0])
3
>>> s_first[0][2]
5

由此看来关于链表递归的深度还是值得讨论的，不过先放一放，暂时把目光放在一些更简单问题上。

递归和递归对象简直是天作之合。我们可以用递归实现很对关于链表的操作。其实，在创建链表类时就已经用到了递归，不过我们的脚步并不止于此。对于链表，我想写一个和list一样的extend函数，用于把两个链表连接起来。

最简单的思路是，把前一个链表的empty改为要加上去的链表。不过目前我们没有直接抵达empty的方法。可以重新从递归的角度思考一下，这个函数该怎么写。

>>> def extend_link(s, t):
        if s is Link.empty:
            return t
        else:
            return Link(s.first, extend_link(s.rest, t))

>>> extend_link(s, s)
Link(3, Link(4, Link(5, Link(3, Link(4, Link(5))))))
>>> Link.__add__ = extend_link
>>> s + s
Link(3, Link(4, Link(5, Link(3, Link(4, Link(5))))))

至此，我们已经发现了链表其实和列表特别像。他们都是有限长度，可以进行元素检索，可以extend。自然，我们也能对列表的map函数和filter函数进行复刻，来做两个属于链表的函数。

那么该怎么写这样的函数呢？递归似乎是万能之法。

>>> def map_link(f, s):
        if s is Link.empty:
            return s
        else:
            return Link(f(s.first), map_link(f, s.rest))

>>> map_link(square, s)
Link(9, Link(16, Link(25)))

map函数完成了，对每个可操作元素调用f，而后产生一个新的链表，完美。那么filter函数呢？

>>> def filter_link(f, s)
        if s is Link.empty:
            return s
        else:
            if f(f.first):
                return Link(s.fisrt, filter(f, s.rest))
            else:
                return filter(f, s.rest)

>>> odd = lambda x: x % 2 == 1
>>> map_link(square, filter_link(odd, s))
Link(9, Link(25))
>>> [square(x) for x in [3, 4, 5] if odd(x)]
[9, 25]

搞定。诶，开始有点感觉了，递归和递归对象。不要停下来，再思考一个问题，列表中join函数由如何复刻呢？暂时先别看答案哦。

>>> def join_link(s, sep):
        if s is Link.empty:
            return ''
        elif s.rest is Link.empty:
            return str(s.first)
        else:
            return str(s.fisrt) +  sep + join_link(s.rest, sep)

>>> join_link(s, ", ")
'3, 4, 5'

递归构建(Recursive Construction)

好了，几个例子下来我们对递归对象有了一定的感性的认识。我们大体知道了该如何去对递归对象写一个递归函数，但具体该如何去描述每一步还是不太清楚。

不用着急，回想一下我们在第一章写的函数count_partitions，用于计算一个整数n，若是分为若干块，每一块最大不超过m共有几种分法。当时我们用树递归计算了结果。不过今天同样的问题，我们来点不一样的。

虽说不一样，其实只是多加入了链表元素罢了。所以第一步基本的递归分析是一样的，即count_partitions(n,m)可以分为两部分：

1. 包含最大分区m的部分：对n-m进行最大整数m的分区，即partition(n-m, m)
2. 不包含最大分区m的部分：对n进行最大整数m-1的分区，即partition(n, m-1)

太熟悉了，太熟悉了，太熟悉了。这简直就是为链表而生的呀！两步计算恰好对应链表的first和rest。

分析完了后，确定基本情况，递归什么时候停下？经过观察发现递归过程中，两个形参都会发生变化，所以两个形参都要找到基本情况。显然形参n是突变的，不断地减去m，当n等于0时，不论用什么分都只有一种分法，即0本身。当然n可能会小于等于0，而我们又无法对这样的n进行分区。同样的，形参m是渐变的，m可能会到达0的位置，而用0是分不动其他数的。好了，我们知道了什么时候递归该停下，这是确定基本情况的第一步。第二步，每个基本情况改返回些什么。为了弄明白这个问题，我们就该知道如何用链表来表示函数的结果。对于这个问题，自然每个人都有不同的看法。这是没有必要统一的，我反而鼓励大家要有自己的想法。在这里我提出自己想法，然而这并不是标准答案。之前我们提到，链表的fisrt也可以是链表。那么我可以想象一个“二维”的链表（这里的“二维”只是一种描述性的说法，并非严谨的专业用词，如果你愿意甚至可以叫它“烤羊肉串”链表），横向的每一个节点都“挂”着一种分区方法。不多废话，上图。

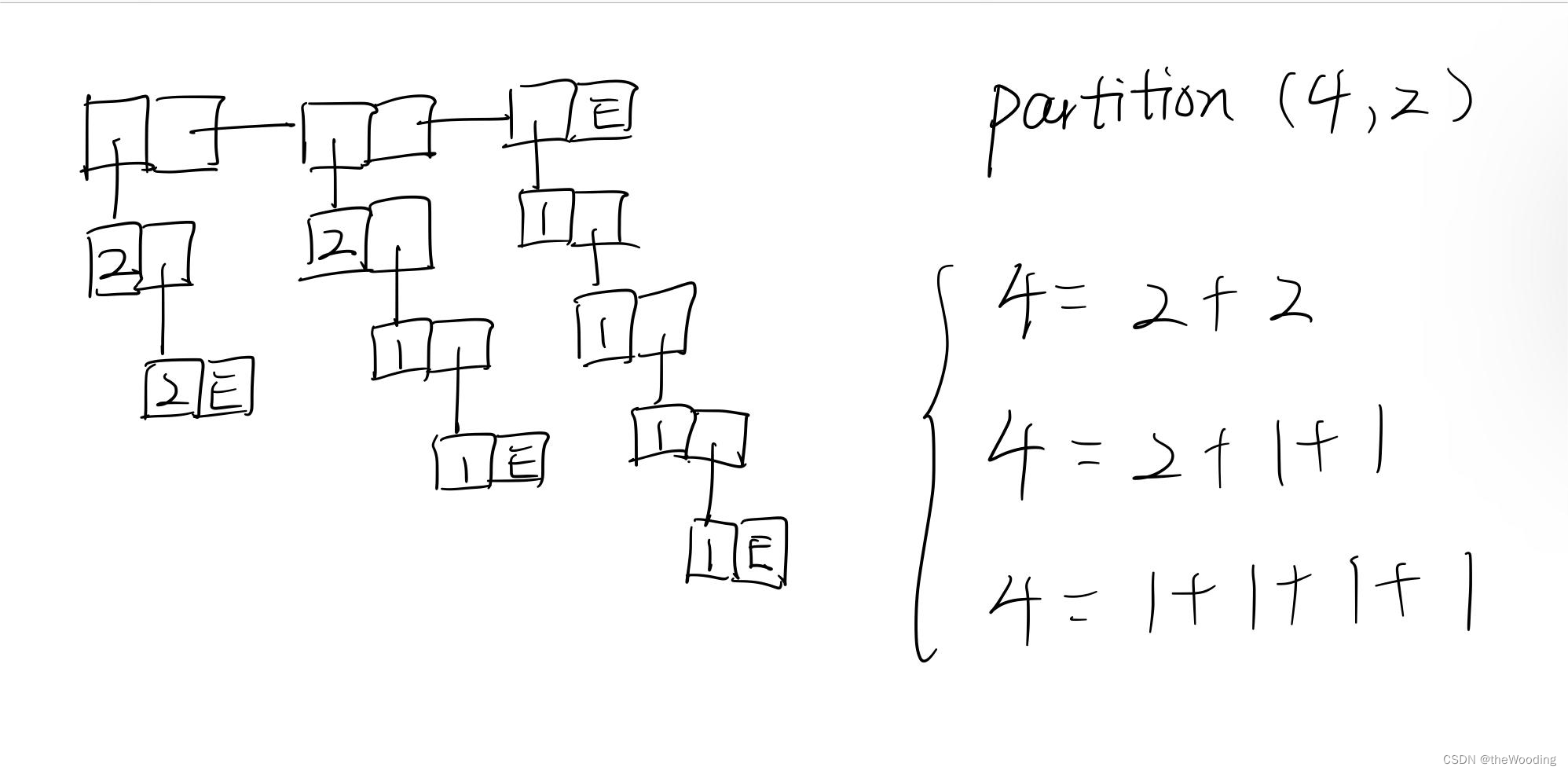
 图中两个方块为一组，左边为first，右边为rest，一组表示一个链表。E是Empty的缩写。这样我们就能很明显的看到如何用链表表示我们的分区结果了。

回到基本情况的问题中，回忆上述的三个递归终点，n<0,n=0与m=0。这三种情况我们应该怎么返回什么呢？大家可以先停一停自己思考一下。

定性考虑，n = 0只有一种分法，就是0本身。不过由于0的特殊性，我们一般不予显示。否则分出100个0也是0，难道我们100个0都要写出来吗？同时，m = 0或者n < 0时在任何时候都是分不动，没法分的。

因此n = 0是返回一个“二维”链表，这个链表上有一个“挂点”（一种分法），但是不“挂”东西（不予显示）。当m = 0或者n < 0时，返回一个没有挂点的“二维”链表。 

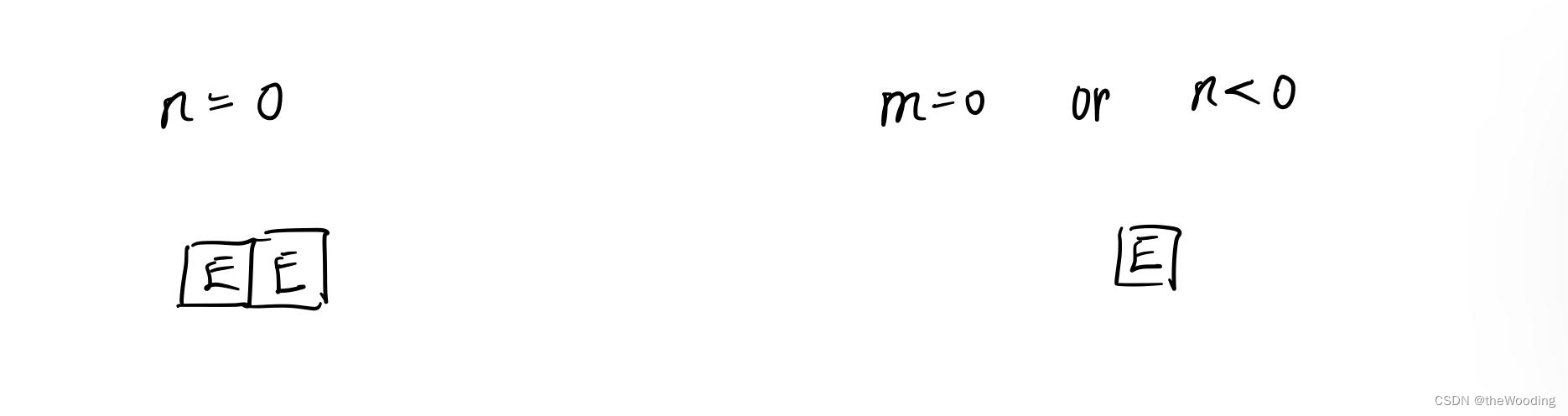
在考虑基本情况后，我们还需根据递归思路完善一下具体细节。在这个例子中，rest等于partition(n,m-1)即partition(4,1)刚好等于最后一个“挂件”，即上面图中“1+1+1”那条竖向链表（此时横向虽然只有一个节点，但我们还是把它看作“二维”链表）。但first，或者说partition(n-m, m)即partition(2, 2)是否等于上面图中前两条竖向链表呢？只要画出他的“二维”链表就能清楚的看到，答案是否定的。自然我们要对partition(n-m, m)即partition(2, 2)做一个简单的处理来满足成为first的要求。具体该怎么做呢？答案不唯一，各位可以自己思考一下。

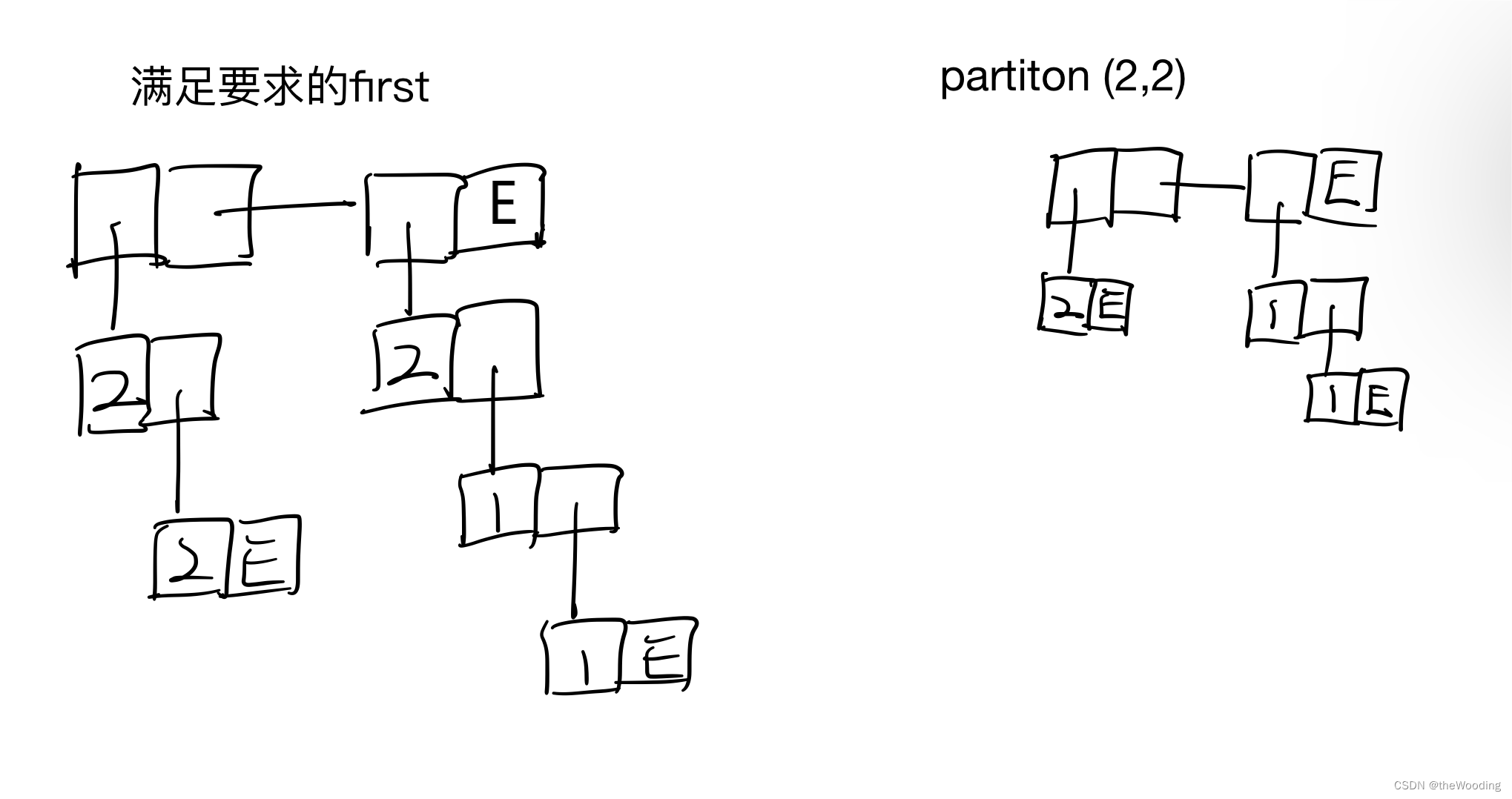
终于，递归细节和基本情况都搞清楚了。我们可以把这个函数的代码写出来了。

>>> def partitions(n, m):
        """Return a linked list of partitions of n using parts of up to m.
        Each partition is represented as a linked list.
        """
        if n == 0:
            return Link(Link.empty) # A list containing the empty partition
        elif n < 0 or m == 0:
            return Link.empty
        else:
            using_m = partitions(n-m, m)
            with_m = map_link(lambda s: Link(m, s), using_m)
            without_m = partitions(n, m-1)
            return with_m + without_m

我们已经清楚的理解了“二维”链表表示分区的方式，同样的，可以创建一个函数专门把这些分区法列举出来。“二维”本质上是一个嵌套链表，我用几何的方式展现出来是为了便于理解。不难看出，链表的每个first都是一个分区法，而first本身是一个子链表，子链表是分区法中所用到的具体分区数。为了便与阅读，我们一行打印一个分区法，每个分区数之间用+号连接起来。当然，得用道之前写的join_link函数。

>>> print_partiton(n, m):
        list = partition(n, m)
        string = map_link(lamba link:join_link(link, '+'), list)
        print(join_link(string, '/n'))

>>> print_partitions(6, 4)
4 + 2
4 + 1 + 1
3 + 3
3 + 2 + 1
3 + 1 + 1 + 1
2 + 2 + 2
2 + 2 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1

2.9.2   树（Tree Class）

树也属于一个递归对象，我们可以同上面一样创建一个树类。

依据我们对树这种结构的了解，很轻易的就能创建一个树类。

>>> class Tree:
        def __init__(self, label, branches=()):
            self.label = label
            for branch in branches:
                assert isinstance(branch, Tree)
            self.branches = branches
        def __repr__(self):
            if self.branches:
                return 'Tree({0}, {1})'.format(self.label, repr(self.branches))
            else:
                return 'Tree({0})'.format(repr(self.label))
        def is_leaf(self):
            return not self.branches

创建完了自然要使用它。一样是我们的老朋友斐波那契数列，一样是一个递归函数，一样是要来点不一样的，一样是不一样只在于引入了我们新创建的Tree类。

>>> def fib_tree(n):
        if n == 1:
            return Tree(0)
        if n == 2:
            return Tree(1)
        left = fib_tree(n-1)
        right = fib_tree(n-2)
        return Tree(left + right, (left, right))

>>> fib_tree(5)
Tree(3, (Tree(1, (Tree(0), Tree(1))), Tree(2, (Tree(1), Tree(1, (Tree(0), Tree(1)))))))

很简单，或许来个其他的？对所有树节点求和？

>>> def sum_tree(t):
        return t.label + sum([sum_tree(_) for _ in t.branches])

>>> sum_labels(fib_tree(5))
10

用到了列表推到式，不过依旧很简单。

还记得我们在讲到“效率”那一节创建的memo函数吗？他大大减少了计算斐波那契数列所需的时间与运行内存。

>>> fib_tree = memo(fib_tree)
>>> big_fib_tree = fib_tree(35)
>>> big_fib_tree.label
5702887
>>> big_fib_tree.branches[0] is big_fib_tree.branches[1].branches[1]
True
>>> sum_labels = memo(sum_labels)
>>> sum_labels(big_fib_tree)
142587180

看不懂吗？没关系，你只需要知道在使用memo之前我们为了计算fib_tree(35)创建了18,454,929个实例，用了memo之后，我们实际上只创建了35个。

2.9.3   集合（Sets）

除了元组，字典和列表之外，python还有另外一种表示一系列元素的方法——集合。不错，这个集合和数学上的那个集合差不多。无序，不重复。

>>> s = {3, 2, 1, 4, 4}
>>> s
{1, 2, 3, 4}

python中的集合能进行很多操作，比如检测元素是否属于，求长度，求交集(intersection方法)并集(union方法)等。

>>> 3 in s
True
>>> len(s)
4
>>> s.union({1, 5})
{1, 2, 3, 4, 5}
>>> s.intersection({6, 5, 4, 3})
{3, 4}

当然远不止这些，还可以检测是否有交集，包含还是包含于（运用isdisjoint, issubset,和issuperset函数）。集合的内容是可以更改的，用 add, remove, discard或者 pop方法。更多的细节就不多加赘述。

实现集合（Implementing sets）

尽管集合属于内置的数据类型，但我们还是可哟通过一定手段去实现一个属于自己的集合。接下来我们会用三种方法实现集合，并且通过分析增长量级来比较不同实现方法的效率。哦！我们会用到上文已经创建的Tree类和Link类，就地取材。主要是因为他们是递归对象，总要再讲讲递归的吧，点题！

无序集合(Sets as unordered sequences)

首先，我们在实现时不考虑元素顺序。选用链表（可以按索引检索元素）来保存集合中的每一个元素。

下一个问题是如何做到不重复呢？必然得有一个检测某元素是否属于该集合的函数。

>>> def set_contains(set, value):
        if set.first = value
            return True
        return set_contains(set.rest, value)

写到这发现我们还差一个基本情况，即什么时候返回False？我们的递归思路是检测第一个元素是否等于value，如果不是，则检测value是否属于去除第一个元素后的子集。这样一个一个求子集后的终点必然是空集。即每一个元素都历遍了，但还是没有找到等于value的元素，这时候就该返回False了。

因此还得先定义一个判断集合是否为空集的函数。首先，确定空集的表示方法。空集，首先从链表的角度思考，它没有第一个元素，也不存在对第二个元素的指向。一个empty还是两个empty？自然是一个empty表示。

>>> def is_empty(set):
        return set is Link.empty        

继续我们的set_contains函数。

>>> def set_contains(set, value):
        if set.first = value:
            return True
        elif is_empty(set):
            return False
        return set_contains(set.rest, value)

大功告成。

>>> u = Link(1, Link(4, Link(5)))
>>> set_contains(u, 0)
False
>>> set_contains(u, 4)
True

到这其实已经基本实现了集合，然后从效率的角度对这种实现方法进行定量分析。

如果设集合的长度为n，那么函数set_contains的增长量级就是θ(n)。

我们已经知道计算流程中增长量级最大的一部分决定了整个程序对计算机资源的消耗，所以我写一个函数，用于把一个元素加入到一个集合中。

>>> def adjoin_set(set, value):
        if set_contains(set, value):
            return set
        else:
            return Link(value, set)

>>> t = adjoin_set(s, 2)
>>> t
Link(2, Link(4, Link(1, Link(5))))

虽然这个函数真正进行连接的工作在最后一步，但他大部分的时间都在检测是否有元素重复。自然，他的增长量级也是θ(n)。

为了让我们的"效率分析"更有说服力，自然是得多加几个实验对象的。再写一个求交集的函数。

>>> def intersect_set(set1, set2):
        if is_empty(set1):
            return Link.empty
        if set_contains(set2, set1.first):
            return Link(set1.first, intersect_set(set1.rest, set2))
        else:
            return intersect_set(set1.rest, set2)

简单分析便可看出，集合1中每个值都要调用一次set_contains函数，调用一次的增长量级为θ(n)。若集合1中有n个值，则调用n次，所以求交集函数的增长量级为。 

有交集自然少不了求并集。该怎么写求并集的函数？各位可以思考一下的出自己的答案。

>>> def union_set(set1, set2):
        if is_empty(set1):
            return set2
        set = union_set(set1.rest, set2)
        if set_contains(set2, set1.first):
            return set
        else:
            return Link(set1.first, set) 
    

不难看出来，union_set函数的增长量级也是。

关于不考虑顺序的集合实现就分析到此。接下来看看考虑顺序的集合实现方法。

有序集合（Sets as ordered sequences）

 有些人就要问了，"集合不是不分顺序吗？"。没错没错，我把一个集合展现给你时会特别告诉你，这几个元素完全是随机顺序陈列出来的。嘿嘿随机随机，计算机怎么做决定我不是我程序猿说了算？不论你输入{1，2，3，4}或者{2，1，3，4}，我都会让计算机告诉你"集合是不讲顺序的，他们是一个东西。"，但是当你想看到这两个集合的具体面貌时，我依旧会让计算机把第二个集合{2，1，3，4}整理（随机陈列）一下，变成{1，2，3，4}给你。这时候你就说"嘿！这不是我输入的集合！"。这时我会让计算机告诉你"都说了集合是不讲顺序的啦，这么较真干嘛呀，他们都是一个东西啦。"

既然如此，我认为应该在我们的表达方式中加一个顺序，从小到大从大到小或者其他什么都可以。我选就从小到大好了。不过具体怎么实现就不细述了，我们就默认这样的顺序已经实现完成了。

然后再一一改写我们上述提到的函数。首先是set_contains函数。既然我们知道了集合中的元素是按从小到大排列的，就不用傻呼呼一个一个来检测是否重复了，那么该改成什么样子呢？

>>> def set_contains(set, value):
        if value < set.first or is_empty(set):
            return False
        elif set.first = value:
            return True
        else:
            return set_contains(set.rest, value)
        

现在来考虑他的增长量级，最坏的情况下，我们依旧要对set中的每一个元素进行检测，增长量级依旧是θ(n)。这么看似乎我们没什么进步，但是增长量级是一个为了追求普遍性而牺牲了细节的概念，哪怕是θ(n)与θ(n)之间也存在着很大的不同。我们在这里讨论的问题正好涉及了细节，增长量级已经不满足我们的需求了。从具体情况出发不难发现，当我们为集合加了一个潜在的排列顺序，就多了一条可利用的规则。这样的规则有时候能更早的告诉我们答案，即什么时候该停止。这在有序集合的set_contains函数中完美体现，我们可以不需要知道"是否相等"，而是知道"小于最小的元素"，就能排除剩下的所有待检测元素。

很快我们就能发现"细节的堆叠成就普遍性"。接下来再试着考虑如何改写intersect_set函数？之前我们在求交集时对两个集合的每个元素都进行了比较，现在我们加了一条规则，是否有更加简便的方法呢？

当我们知道了集合有着从小到大的潜在顺序，那么对于set1中的某个元素来说，就不需要与set2中的每个元素比较，当遇到任何比他大的元素，就可以停止脚步了。这条规矩对set2也成立。所以我们可以双管齐下。 

>>> def intersect_set(set1, set2):
        if is_empty(set1) or is_empty(set2):
            return Link.empty
        element1 = set1.first
        element2 = set2.fisrt
        if element1 == element2:
            return Link(element1, intersect(set1.rest, set2.rest))
        elif element1 < element2:
            return intersect_set(set1.rest, set2))
        else: # element1 > element2
            return intersect_set(set1, set2.rest)
            

接着分析一下这个函数的增长量级。我们很容易因为"有两个集合参与这场演出"就得出答案是。但是只有n*n才会等于，n+n只会得到2n。如果我们考虑最坏的情况，比如求{1，3，5，7}和{2，4，6，8}的交集（看起来很傻）。我们只是同时历遍了两个链表罢了，最终的操作数是两个链表的长度和而不是长度积。所以，增长量级为θ(n)。芜湖！这可是个大进步啊！

adjoin_set函数和union_set函数又有什么样的改变呢？这就留给大家自己思考了。

二叉树实现集合（Sets as binary search trees）

只是加了"从小到大"一条简单规则，就能让我们的函数优化这么多。如果我们把这条规则变得更加严谨优化效果会不会更上一层楼呢？

如果用树来实现集合，我们便能提出一个新规则：左边的分支树是比节点元素小的元素组成的集合，右边则反之。

比如集合{1，3，5，7，9，11}就由以下几种表达方式。

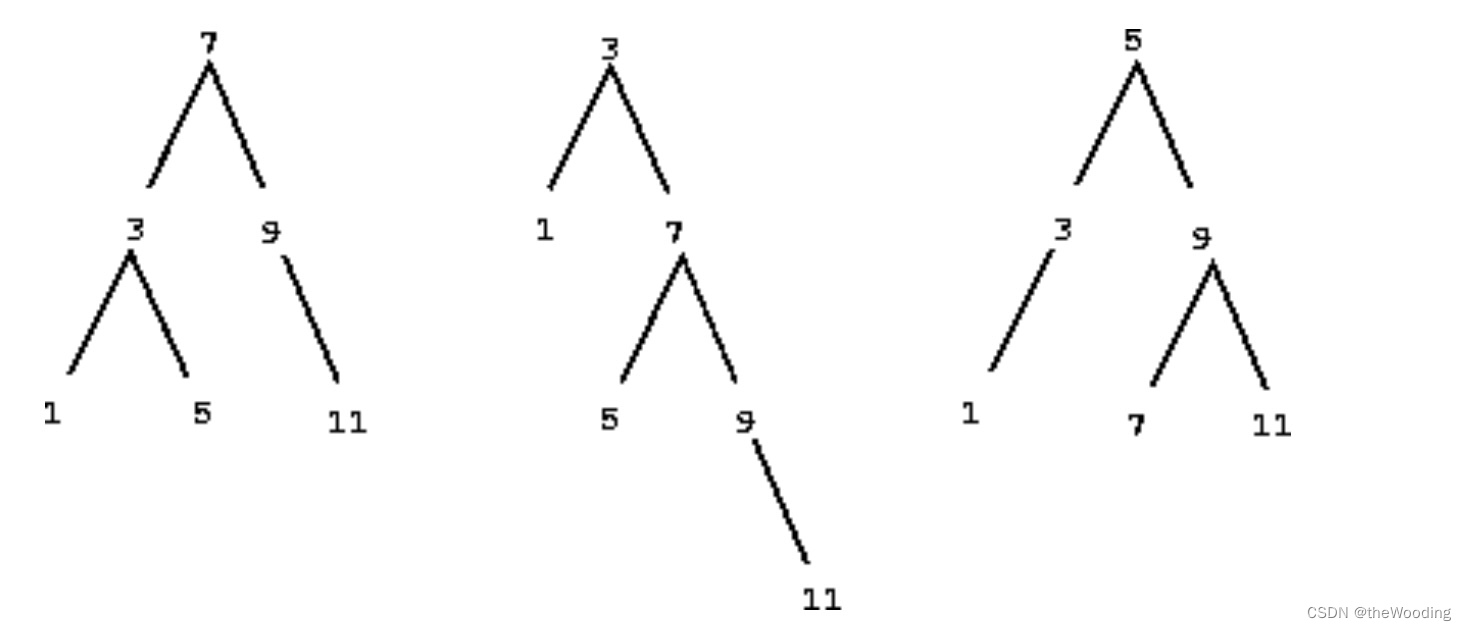
 现在考虑一个问题，如何重写set_contains函数呢？

>>> def set_contains(set, value):
        if is_empty(set):
            return False
        elif value = set.label:
            return True
        elif value < set.label:
            return set_contains(set.branches[0], value)
        else: # value > set.label:
            return set_contains(set.branches[1], value)

嚯嚯，简直是太妙啦！让我们来看看这个函数吧。我们打破抽象壁垒去思考的话，发现每检测一次value与set节点值的关系，就能排除掉一个分支上的所有元素！如果这个集合树是对称的，那么每次就可以排除掉一半！这样的效率和前面的比起来简直太恐怖了！

让我们分析一下他的增长量级。假设集合set的长度为n，最坏的情况自然是走到树叶。即n  /2 /2 /2 /2 /2 /2 /2一直除2直到得到0（整除），即最坏情况下，第一次递归待检测集合长度为n，第二次为n/2，第三次为n/4（如果有第三次的话）……直到最后一次待检测集合为空集，总共走了lg n（算法中，lg的默认底数不是10，而是2）次递归。 所以这个函数的增长量级为。女士们先生们，这效率是多么的惊人（和之前相比）！

不要停下脚步，让我们继续写adjoin_set函数看看。

>>> def adjoin_set(set, value):
        if set is None:
            return Tree(value)
        elif value > set.entry:
            return Tree(set.entry, set.left, adjoin_set(set.right, value))
        elif value < set.entry:
            return Tree(set.entry, adjoin_set(set.left, value), set.right)
        else: #value = set.entry
            return set

显然，这个函数的增长量级也是​​​​​​​。因为我们的每次递归都会把待操作集合缩小一半，只要我们的集合是对称的。

但我们如何保证这个集合是对称的呢？就算我们在定义上下功夫，保证每个集合都必须定义成对称的，但每当调用一次adjoin_set函数时，我们都会给一个集合加上新的元素，这必然会破坏一个集合树的对称性。或许我们需要一个函数，专门用于把一个随机形式的集合树转变为对称的集合树。

集合树的交集和并集如何求？可以考虑把树转换成有序的链表进行求交集或者并集，或许还有其他方法？谁知道呢，教给大家自己思考好了。

python集合的实现（Python set implementation）

在python中，内置集合类型的实现并不依靠以上所述的方法。在使用python内置集合，我们调用的类似"set_contains"与"adjoin_set"函数是所耗费的计算机资源是固定的。他是用了一种名为"哈希（hashing）"的技术，这是另一门课的内容。在python的内置集合中，不能有任何可变数据类型，就是说集合里不能有列表，不能有字典，不能有集合等等。不过python中有一个内置frozenset类，为了嵌套定义集合而生。frozenset可以进行关于set类除了修改之外的任意操作。