拉格朗日乘子法

最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值(因为最小值与最大值可以很容易转化，即最大值问题可以转化成最小值问题)

一、无约束条件

                               
这是最简单的情况，解决方法是函数对变量求导，令求导函数等于0的点可能是极值点。将结果带回原函数进行验证。

二、等式约束条件

设目标函数为f(x)，约束条件为h_k(x)，形如:

　　s.t. 表示subject to ，“受限于”的意思，l表示有l个约束条件。

　　　　　　　　

则解决方法是消元法或者拉格朗日法。这里主要讲拉格朗日法，后面提到的KKT条件是对拉格朗日乘子法的一种泛化

例一：
 例如给定椭球：

                         

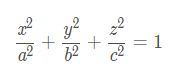
在下 ，求f(x,y,z)=8xyz的最大值。

当然这个问题实际可以先根据条件消去 z (消元法)，然后带入转化为无条件极值问题来处理。但是有时候这样做很困难，甚至是做不到的，这时候就需要用拉格朗日乘数法了。 首先定义拉格朗日函数F(x)：

     （其中λ k \lambda kλk是各个约束条件的待定系数。）
然后解变量的偏导方程：

                                                        

 如果有i个约束条件，就应该有i+1个方程。求出的方程组的解就可能是最优化值（高等数学中提到的极值），将结果带回原方程验证就可得到解。

回到上面的题目，通过拉格朗日乘数法将问题转化为：

 

 对F(x,y,z,λ)求偏导得：

 联立前面三个方程得到b x = a y 和az=cx,带入第四个方程解之
 

 

 带入解最大体积为：

 再举一个便于理解的例子

例二：

求此方程的最大值：

 

s.t

因为只有一个未知数的限制条件，我们只需要用一个乘数λ.

将所有L方程的偏微分设为零，得到一个方程组，最大值是以下方程组的解中的一个：

 

 

由上面三个条件可以知道，取到最优解时，必然满足等式约束。

解得             

 实际上这边没必要对求偏导，求了也就是原来的等式约束。

 

三、不等式约束条件

设目标函数f(x)，不等式约束为g(x)，有的教程还会添加上等式约束条件h(x)。此时的约束优化问题描述如下：

                                             

则我们定义不等式约束下的拉格朗日函数L，则L表达式为:   

其中f(x)是原目标函数，hj(x)是第j个等式约束条件，λj是对应的约束系数，gk是不等式约束，uk是对应的约束系数。
 常用的方法是KKT条件，同样地，把所有的不等式约束、等式约束和目标函数全部写为一个式子L(a, b, x)= f(x) + ag(x)+bh(x)

KKT条件是说最优值必须满足以下条件：

L(a, b, x)对x求导为零；
h(x) =0;
a*g(x) = 0;
 求取这些等式之后就能得到候选最优值
该方法适用于约束条件下求极值的问题。对于没有约束的极值问题，显然，如果某一点是极值的必要条件是该点的各方向的偏导数皆为零，也就是说，如果偏导数不全为零，那么就不可能是极值。