基于Graham扫描线算法的更加强大的凸包算法——Melkman算法

大家好，这里是蒟蒻霞客，thewalker88
今天我来给大家讲解一种OI中很少有人使用，然而在我看来比常用的Graham扫描线算法更为强大的算法——Mlekman算法
为了学习这个新算法，你需要如下前置技能：
1），会计算几何基础，尤其是叉积
2），掌握Graham扫描线算法求凸包
如果你不会如上前置技能，网上各路神犇的关于此的讲解很多，如果能够先点亮这些前置技能，理解这篇博客无疑会更加轻松

那么，如果现在你们已经点亮了上述前置技能…
我们开始吧！！！
对于点集求凸包，Graham扫描线是可以在O（nlogn）的时间内完美解决的，而且很容易可以知道点集求凸包的时间复杂度下界是O（nlogn）。
但是，如果是求简单多边形的凸包呢？

简单多边形：没有自交边的多边形即为简单多边形（凸多边形，凹多边形皆可）

问题：
平面上有一个简单多边形，沿着多边形的边，按照逆时针的顺序给出多边形的顶点的坐标，要求你求出此多边形的凸包。

如果你还记得对于点集的凸包我们是如何解决的的话，我们先是将点按照某种顺序排序（水平序或极角序），再从某个一定在凸包上的点上的开始扫描。
但是我们注意到，对于按顺序给出的简单多边形上的点，***他们本身就带着一个序！！！***（感性理解一下）
因此，我们求简单多边形的凸包，只需要从某个必在凸包上的点开始用Graham扫描线计算一圈，就可以求出此多边形的凸包了。。。。。
看起来是这样，其实并不是
因为Graham 无法处理如下图的简单多边形！

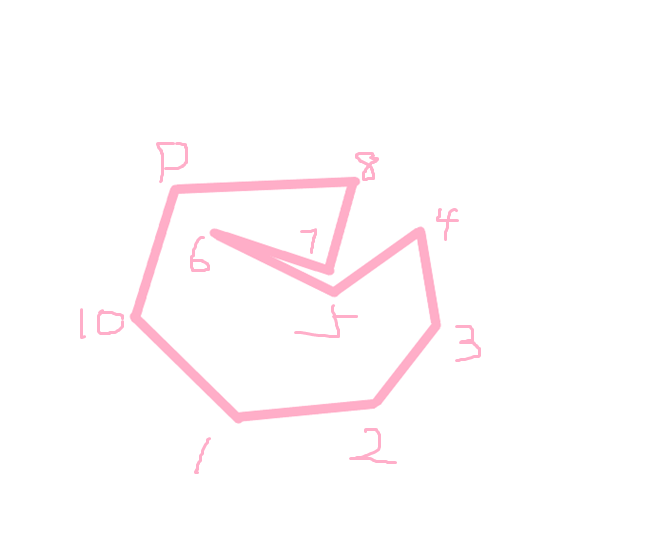
对于这个多边形，我们从一号顶点开始扫描，从1一直到6都是没有问题的，此时栈里面从底到顶的顶点编号是1、2、3、4、6
此时考虑点7，我们惊讶的发现，***线段46到线段67是逆时针旋转的，这意味着点7不会造成弹栈 ***，最后，我们求出的凸包将是，下图中的红色部分

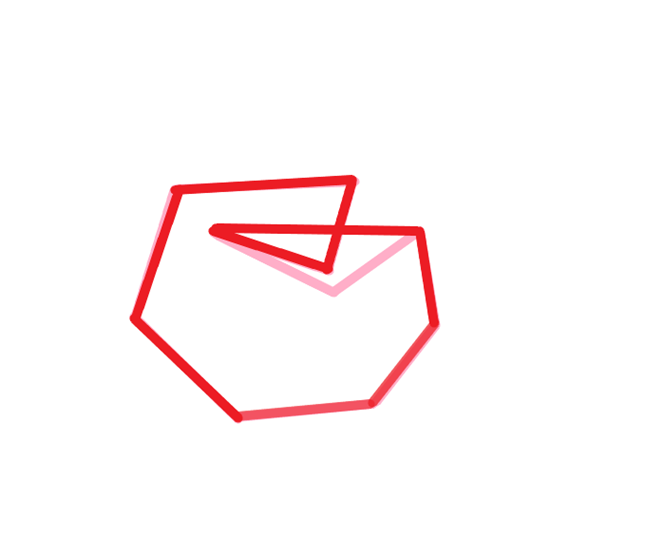
可见，Graham对于此类多边形求得的凸包将是一个复杂多边形，显然错误
因此，我们只能将其像处理点集一样，先排序再搞。
然而，这样不仅没利用上简单多边形自带的序，而且复杂度还是O（nlogn）的，很不好

因此，我现在来介绍一种***由Melkman在1987年发明的，可以在O（n）的时间复杂度下求出正确的，简单多边形的凸包的Melkman算法***

这个算法是**基于Graham扫描线算法的***，他们的大体思路相同，但是不同之处在于，Graham使用一个栈来维护凸包，而Melkman使用一个双头队列来维护凸包，每次不仅仅维护队列头的凸性，也维护队列尾的凸性，因此，它得到每时每刻都包含当前考虑过的所有的点的凸包
下面我们模拟一下
对于一个n个点的多边形，我们开一个大小为2n的deque（即双头队列），设bot为队列尾，top为队列头，bot初始值为n-1，top初始值为n
我们把点1从前插入队列，同时top++，接下来，由于队列里只有一个点1，我们可以直接把2从队列头插入和把2从队列尾插入***注意，从现在起每时每刻，队列头和队列尾的点总是同一个，也就是当前凸包里的最后考虑的点***
接下来我们插入点3
我们说过，要在队列头和队列尾都维护凸性，如果队列头不是凸的，在队列头弹栈（top–），如果队列尾不是凸的，我们在队列尾弹栈（bot++），我们写程序的时候，在队列头维护一下，然后入栈，之后在队列尾维护一下，然后入栈，所以最后，我们的队列会是3 1 2 3或者3 2 1 3
这是头三个点
我们现在来考虑点4，我们看，队列头和队列正数第二个点所连成的直线，队列尾和队列倒数第二个点所连成的直线，以及剩下的凸包上的边们，会把平面分为5个部分，看图

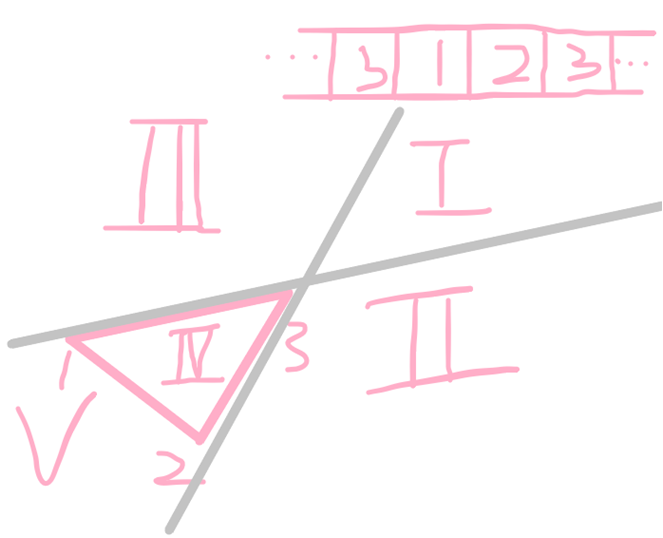
如果第四个点落在区域II，说明对列头不合法了，在队列头弹栈，如果在区域III，我们要在队列尾进行维护，如果在区域I，我们要把队列的头和尾一起进行维护，如果在区域IV说明这个点是当前所求得的凸包内部的点，明显对答案没有贡献，我们此时直接忽略这个点去看第五个点（上次用Graham跑凸包时的错误可被此情况排除）
那么，如果点落在区域V呢？？？
并不会落在区域V！
因为我们是个简单多边形，如果在区域V有点，则必然产生自交边，这是违背简单多边形的定义的。
如此进行下去，直到我们将所有的点考虑一遍，此时bot+1到top-1就是凸包上的点
时间复杂度很明显是线性的，因为每个点最多进栈出栈一次
而且此算法还是个在线算法，可以随时接收新的点，并且我最开始塞入队列中的点不必非得在凸包上，相比之下，这个算法比Graham妙得多
来看一下蒟蒻丑到不行的代码

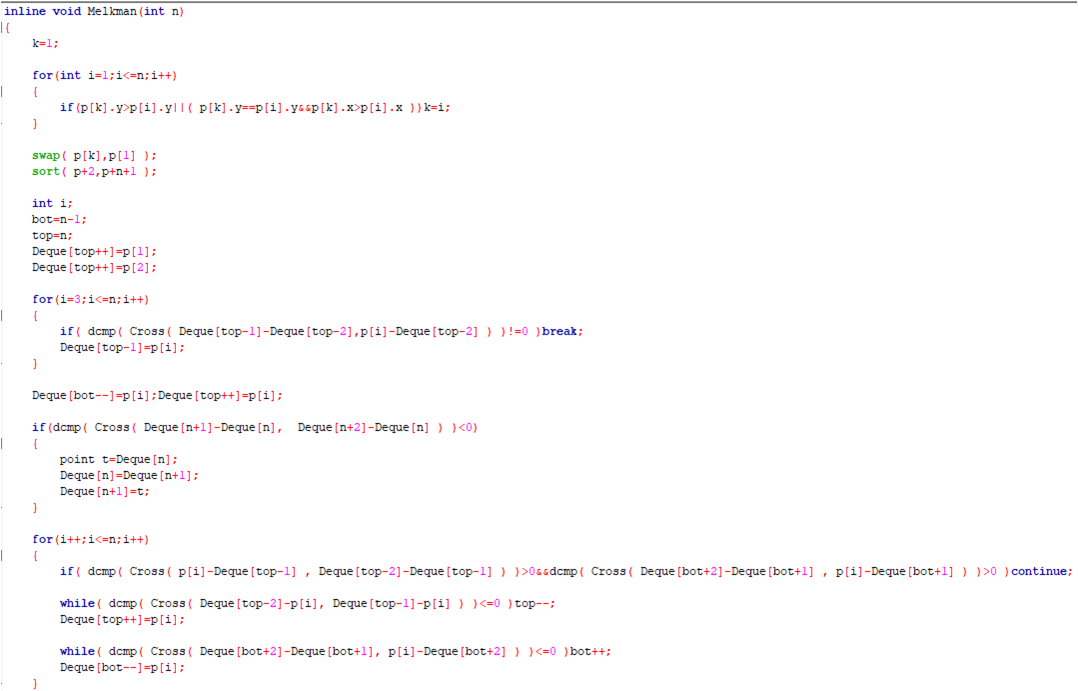
实现细节：判断在什么区域时，只需要先排除IV区，接着队列头队列尾分别判断即可，无需细究究竟是什么区域
希望您有收获
我的QQ号是1145101354 ，欢迎大家加我来讨论问题（请注明来自CSDN）

注：本文中贴出的代码与文中的代码实现并不是完全一样
此代码是先将点1，2入队，如果1，2，3时逆时针的，则直接入3（结束后队列为：”3，1，2，3“），否则将1，2调换位置，然后入3（结束后队列为：”3，2，1，3“）
然而18.03.09晚在我正在给东北的众神犇口胡的时候，神犇Camouflager 提出，2也如同之后的点一样前后都加入队列，然后再慢慢弹栈，这样对正确性没有影响，而且代码似乎能好写点，经过思考觉得神犇就是神犇，说的话挺有道理，因此本文中对算法描述的时候采用了Camouflager的想法。这是与原论文不一样的地方