概率图模型(06): 概率图双重对偶视角 || 马尔可夫网 & 条件随机场及应用

　　本博客中 PGM 系列笔记以 Stanford 教授 Daphne Koller 的公开课 Probabilistic Graphical Model 为主线，并参阅 Koller著作及其翻译版对笔记加以补充。博文的章节编号与课程视频编号一致。
　　博文持续更新（点击这里见系列笔记目录页），文中提到的资源以及更多见 PGM 资源分享和课程简介。

　　本文围绕马尔可夫网（MNs），讨论三方面内容：

　　1）MNs 的模型：成对马尔可夫网，吉布斯分布，条件随机场，对数线性（Log-Linear）模型，伊辛（Ising）模型，度量马尔可夫随机场。作为模板的共同特征提取。
　　2）MNs 的结构：独立关系，因子分解，以及两者等价性。BNs 和 MNs 的相互转化，概率图统一的双重对偶视角，I-map，P-map 的存在唯一性，通过图完美捕捉分布中的所有独立性。
　　3）MNs 的应用：详解 CRFs 应用的建模思路和方法分析：图像去噪，图像分割，三维重建，自然语言处理。

---

1 成对马尔可夫网

1.1 形式化表示

• 成对马尔可夫网 ( Pairwise Markov Networks ) : 一个以随机变量 $X_i$ 为节点无向图网络，每一条边代表一个因子 $\phi_{ij}(X_i,X_j)$.

  它是马尔可夫网中最简单的一种，是因子定义在成对变量上的分布。

1.2 简单例子

  右下图表示了一个由四个随机变量 $A,B,C,D$ 组成的成对马尔可夫网。网络中的因子均定义在只由两个成对随机变量组成的变量集上，即 $D_1=\{A,B\}, D_2=\{B,C\}, D_3=\{C,D\}, D_4=\{D,A\}.$

1.2.1 联合分布

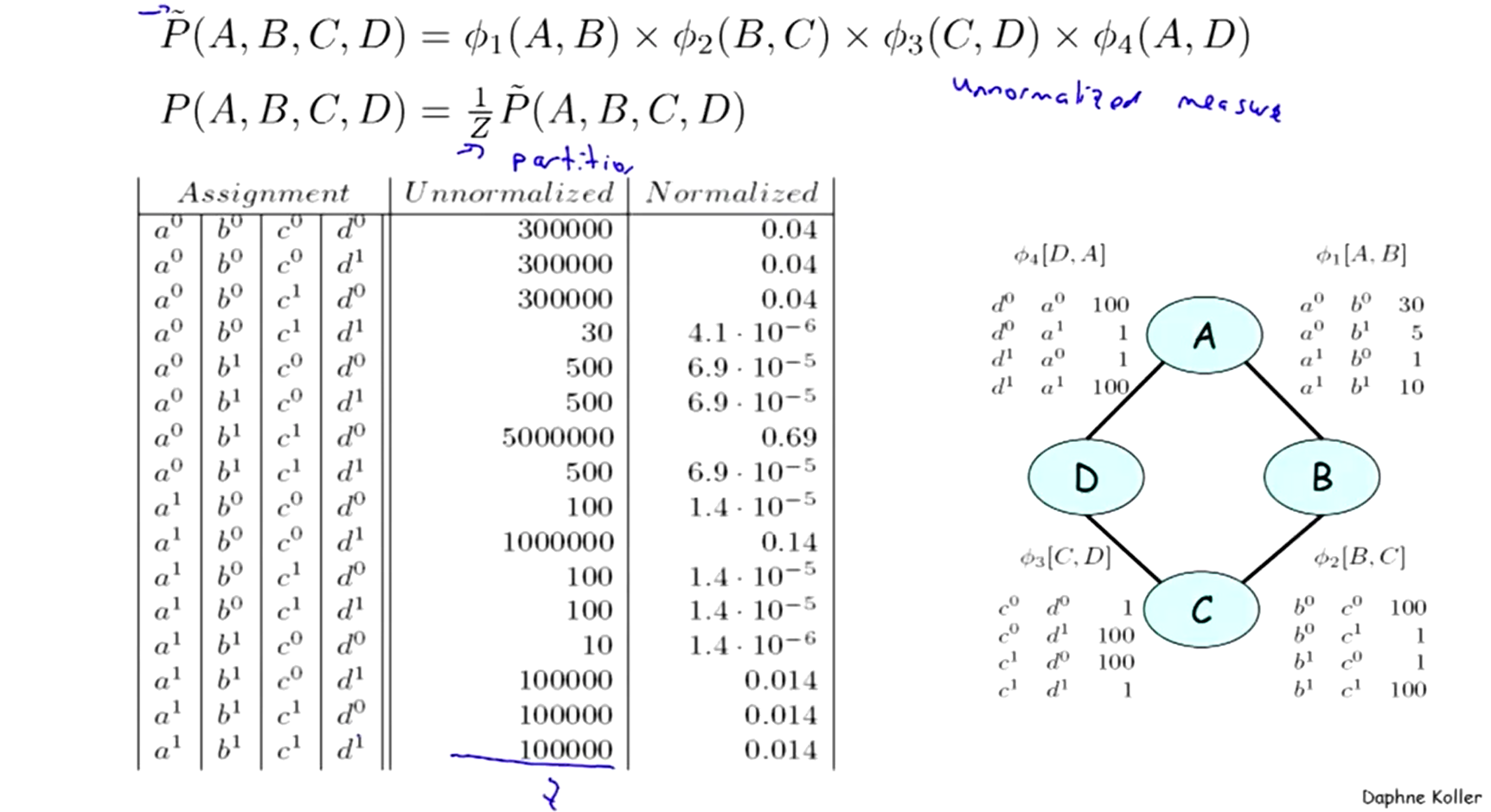
  左上图是由所有（四个）因子相乘计算得到的右上图例子的联合分布表。表中“unnormalized”列的因子积是未经过归一化的，所以这些值只是因子积，还不算是严格意义上的一个分布表示。

1.2.2 配分函数

   为了进行归一化，计算上图例子中的配分函数（partition function）$Z =\sum\limits_{A,B,C,D}\widetilde P_Φ(A,B,C,D)$，即“unnormalized”这一列因子积值的加和。得到了“normalized”列即为该网络的联合分布表。

1.3 如何理解因子

1.3.1 因子和什么有关

　　在成对马尔可夫网中，从因子能否看出其分布的独立性？能否尝试将因子理解为变量在其辖域上的边缘分布？
　　如果这样，我们通过观察任何一个因子，都有可能相信由马尔可夫网定义的整体联合分布与因子定义的分布有相似的特性（比如某两变量间边上的因子很小，那么这两个变量倾向于边缘独立）。
　　然而答案是否定的：

  答案是和以上三个都无关，所以因子的特殊含义就是本文马尔可夫网要讲的内容。

1.3.2 从因子到联合分布

　　下面我们继续上文的例子，来解释：为何难以将边缘独立性和因子关联起来？

• 边缘分布：划掉某些因子后考虑剩余因子上的联合分布，即为剩余因子的边缘分布，如左下表1。

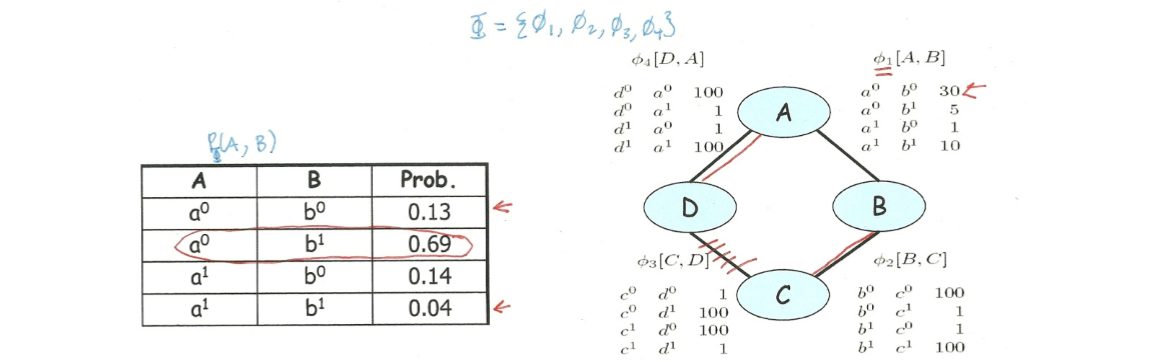
　　如上左图为计算得 $A,B$ 的边缘分布，而其中概率最小的 $(a^0,b^0)$ 在因子 $\phi_1(A,B)$ 中却是概率最大。即我们观察到，某个特定因子所传达的变量间关系，呈现在联合分布中时，可能会被其他更强的因子淹没掉。即从因子到最终推得联合分布的过程中，每个个体因子的部分信息被淹没了，而留下来的是网络作为整体的信息。
　　通过这个例子需要明确，一个因子仅仅是影响联合分布的一个因素，而作为网络整体的联合分布必需将所有因子的影响考虑进去。网络的联合分布是所有因子共同作用产生的结果。

1.4 更大的网络例子

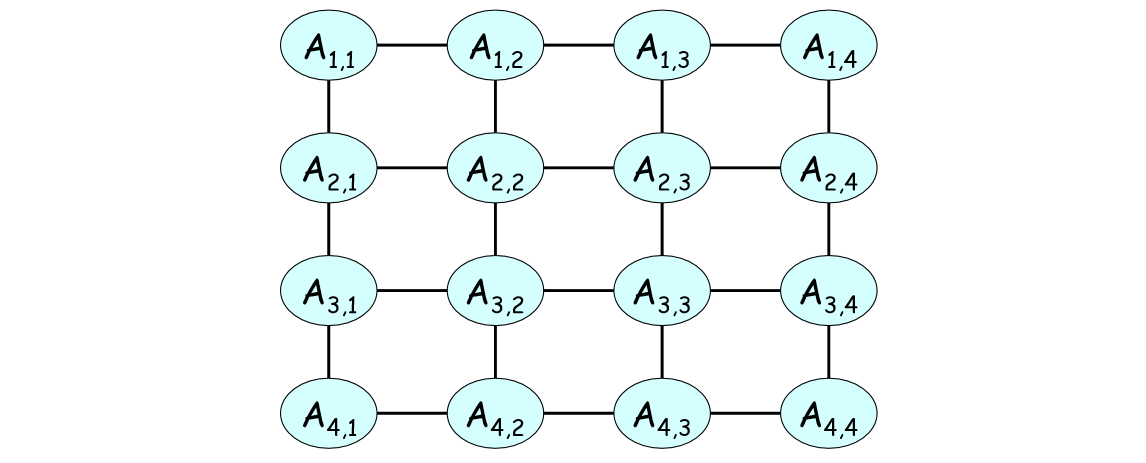
　　值得一提的是，是否是成对马尔可夫网由因子的选取决定。比如下图，只要我们将因子选取在成对变量上，它就是一个更大的成对马尔可夫网例子。

2 吉布斯分布

2.1 成对马尔可夫网的局限

　　成对马尔可夫网不能表示变量的所有组合：表示一个 $n$ 个节点，每个节点有 $d$ 个属性取值的马尔可夫网所需的变量个数为 $O(n^2d^2)$。但如果节点任意搭配所需使用的变量个数是 $O(d^n)$，远大于前者。即成对马尔可夫网的所能表达的分布个数远小于实际网络可能的分布个数。

　　所以不是每一个分布都可以表示为成对马尔可夫网。

2.2 形式化表示

　　这里给出马尔可夫网的形式化描述，可以先不详细看。对于一个以随机变量 $X_i$ 为节点无向图网络，定义：

• 变量集：网络中的随机变量被划分为多个变量集，记作 $D_k=\{X_{k_{1}},...,X_{k_{l_k}}\}$.
• 因子 ( factor )：因子 $\phi$ 是定义在随机变量集合 $D$ 上值域为实数的函数，通常我们关心非负因子；
• 辖域 ( Scope )：变量集 $D$ 称为因子 $\phi$ 的辖域。记作 $Scope[\phi]$；
• 因子乘积: 将两个有公变量的变量集按其公共变量的统一属性对应的因子做乘积，如 $\psi(X,Y,Z)=\phi_{X,Y}(X,Y)\phi_{Y,Z}(Y,Z)$.
• 因子的联合分布：因子的联合分布由其辖域上的因决定，即 $\phi _k(D_k)=\prod\limits_{l=1}^{l_k}\phi _{l}(X_{l})$.
• 网络的联合分布：马尔可夫网的联合分布由其所有因子的联合分布 $\phi _k(D_k)$ 之积决定，即 $P_{\Phi}(X_1,...,X_n)=\prod\limits_{k=1}^m\phi _k(D_k)$.

   可以看到，上述我们得到的网络联合分布概率的表示，在严格意义上还不是一个分布，因为这个概率之和不一定为 1，所以这里需要对网络进行归一化。我们定义

• 配分函数 ( partition function )：用于联合分布表示中的归一化参数，即 $Z =\sum\limits_{X_1,...X_n}\widetilde P_{\Phi}(X_1,...X_n)$

  现在我们可以给出上述马尔可夫的网联合分布一个严格表示

$$式 (1) :P_{\Phi}(X_1,...X_n)=\frac{1}{Z}\widetilde P_{\Phi}(X_1,...X_n).$$

2.3 吉布斯分布

  式 (1) 所表示的分布被称作一个被因子集 $\Phi ={\phi_1(D_1),...,\phi_K(D_K)}$参数化的吉布斯分布，记作 $P_{\Phi}$.

与成对马尔可夫网这种因子定义在成对变量上的马尔可夫网相比，可以将吉布斯分布直观理解为

• 吉布斯分布 ：是马尔可夫网中因子定义在变量集的分布。

  并且吉布斯分布将分布表示为了因子的乘积，提出了一种对于分布的分解表示方式。

2.4 由因子导出图

　　既然网络联合分布由因子决定，而吉布斯分布是因子定义在变量集上的分布。那么，是否可以由吉布斯分布的因子来推出其相应图的结构呢？
　　如图，给出两个因子，其导出的马尔可夫网络（Induced Markov Network）如右图。

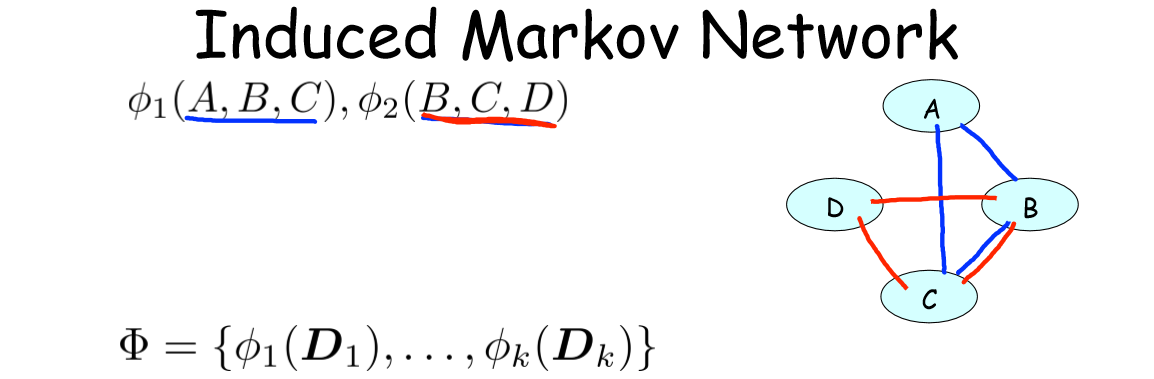
　　一般地，给出如上因子集，和其对应的一组随机变量 $X_i$，当存在辖域 $D_k$ 满足 $X_i, X_j\in D_k$ 时，导出的马尔可夫网 $\mathcal H_{\Phi}$ 中有 $X_i-X_j$ 这条边。即属于同一辖域的变量两两之间有边连接（Induced MN has an edge $X_i-X_j$ whenever they appear together in the same scope）。

2.5 因子分解

  对于给定的一个分布 $P$，是否可以用吉布斯分布来表示它呢？

• 因子分解：如果存在一个因子集 $\Phi ={\phi_1(D_1),...,\phi_K(D_K)}$ 使得 $P_{\Phi}=P$，则称分布 $P$ 可以由马尔可夫网 $\cal H$ 因子分解。

  2.6 从图到因子分解

  　　现在反过来考虑，给定一个吉布斯分布对应的图，是否可以推出其因子集（因子分解）？
  
  　　答案是“All of above”，即从图读不出因子分解，即马尔科夫网的结构不能完全地刻画（fully specify）出分布的特性。

  　　我们看到，不同的吉布斯分布（和其对应的因子分解）可能导出相同马尔可夫网络（Induced MN）图，且这些图性质无差别。即吉布斯分布的表达能力（expressive power）要强于图结构的表达能力。
  　　这很好理解，前文 2.1 部分已经阐述了成对马尔可夫网的所能表达的分布个数远小于实际网络可能的分布个数，而这里的成对马尔可夫网实际上和导出图的结构一一对应（成对 MN 的因子与导出图的边一一对应）。

  　　注：“图的结构”怎么理解？由于马尔可夫网是无向图，所以图的结构就完全有图中的边来决定。两个节点相同的图（随机变量一定），边一一对应则两图结构相同。

  2.7 影响的流动 ( Flow of Influence )

  　　同贝叶斯网一样，马尔可夫网中也存在节点间影响的流动，而且这里的 Flow 似乎更自由。
  　　由于是无向图，故当所有节点均未被观测时，影响的流动与节点类型无关（即不区分有向图中的父子节点），只要两节点间存在路径（迹），影响就可以流动。当有部分节点被观测时，只要两个节点间某一条迹上节点均未被观测，该迹上仍可以有影响力流动，并称该迹是激活（active）的。

  • 若节点均未被观测，影响可以在任何迹中流动。
  • 若有节点被观测了，影响可在激活的迹中流动。

    即马尔可夫网中影响沿着任何无向迹流动，仅当我们对迹中某些节点取条件时，流动才会受到阻碍。

  2.8 重点总结

  • 吉布斯分布将分布表示为了因子的乘积；
  • 由因子导出的马尔可夫网中，属于同一辖域的变量两两之间有边连接；
  • 马尔可夫网的结构不能完全地刻画出分布的特性；
  • 马尔可夫网中影响沿着任何无向迹流动，仅当我们对迹中某些节点取条件时，流动才会受到阻碍。

  3 条件随机场

  　　条件随机场（CRF, Conditional Random Fields）与马尔可夫网（MN, Markov Network）结构类似，但目的不同，它采取与吉布斯分布不同的配分函数去归一化分布。

  3.1 朴素贝叶斯网的不足

    当一个问题的 features 为 $X,Y$，且 $X$ 已知（Obeserved），$Y$ 未知（Target）。朴素贝叶斯（NB）的求解是假设 $X$ 这组特征