算法学习【7】常见排序算法

        部分内容参考：http://blog.csdn.net/whuslei/article/details/6442755

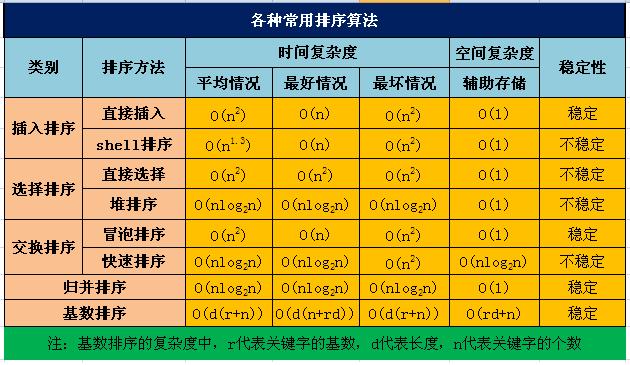
        常见排序算法的时间复杂度：

        注：图片来源http://blog.chinaunix.net/uid-21457204-id-3060260.html

        在平均时间复杂度为O(nlogn)的排序算法中，归并排序是唯一稳定的。

        在平均时间复杂度为O(n*n)的排序算法中，选择排序是唯一不稳定的。

        最好时间复杂度为O(n)的排序算法：插入排序、希尔排序、冒泡排序。

        时间复杂度和数据的初始排列无关：堆排序、归并排序、选择排序。

        快速排序、基数排序需要额外空间。

        1、冒泡排序

        每次遍历比较相邻元素大小，通过交换相邻元素将最大元素后移。

	public static void myBubbleSort(int[] arr, int len){
		for(int i=0;i<len-1;i++){
			boolean flag = true;
			for(int j=0;j<len-1-i;j++){
				if(arr[j]>arr[j+1]){
					swap(arr, j, j+1);
					flag = false;
				}
			}
			if(flag)
				return;
		}
	}

        相邻元素相等时不交换。在第一次遍历中加上标志位flag，才能使最好情况达到O(n)。

        2、选择排序

        每次遍历直接找出最小元素然后与首位置元素交换。

	public static void mySelectSort(int[] arr, int len){
		for(int i=0;i<len-1;i++){
			int minNo = i;
			for(int j=i+1;j<len;j++){
				if(arr[j]<arr[minNo]){
					minNo = j;
				}
			}
			swap(arr, minNo, i);
		}
	}

        3、插入排序

        前n个元素已排序，现将第n+1个元素插入到前n个元素中，因此从后向前依次与前一位元素比较。若前一位小于等于元素n则停止，否则将前一位元素后移。为了避免交换相邻元素带来的额外开销，可将待插入元素暂存于temp，若前一元素大于元素n，直接赋值arr[n]=arr[n-1]，覆盖原来待插入元素即可。

	public static void myInsertSort(int[] arr, int len){
		for(int i=1;i<len;i++){
			int temp = arr[i];
			int j=i-1;
			for(;j>=0;j--){
				if(arr[j]<=temp){
					break;
				}else{
					arr[j+1]=arr[j];
				}
			}
			arr[j+1]=temp;
		}
	}

        4、快速排序

        选取一个数(通常取第一个数)，将数组分成两部分，一部分小于等于该数，一部分大于该数，然后采用递归思想，再对这两部分分别拆分，当拆分后数组长度小于2时递归停止。

	public static void myQuickSort(int[] arr, int left, int right){
		if(right-left<=0){
			return;
		}
		int pivot = arr[left];
		int i = left;
		int j = right;
		while(i<j){
			while(arr[j]>pivot&&i<j)
				j--;
			while(arr[i]<=pivot&&i<j)
				i++;
			swap(arr,i,j);
		}
		swap(arr,left,i);
		myQuickSort(arr,left,i-1);
		myQuickSort(arr,i+1,right);
	}

        5、希尔排序

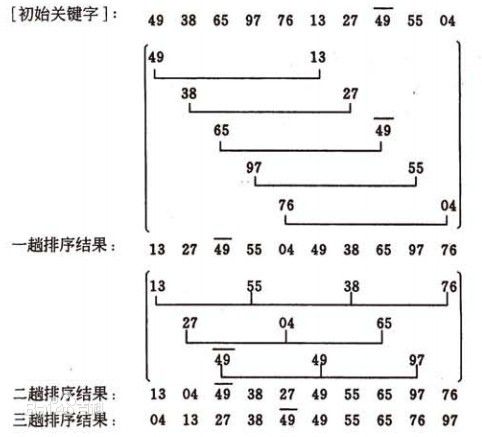
        希尔排序是插入排序的一种改进。它将记录按下标的一定增量分组（例，选择步长d=3，则将arr[0]、arr[3]、arr[6]作为一组，arr[1]、arr[4]、arr[7]作为一组，...），然后对每组进行直接插入排序。然后将步长逐步减少，每组元素个数越来越多，当步长减至1时，整个数组合成一组，排序结束。希尔排序的时间复杂度与所选步长有关，一般取初始步长d = n/2，然后逐步减半。

        示例如下，图片来自百度百科。

	public static void myShellSort(int[] arr, int len){
		int d = len/2;
		while(d>0){
			for(int i=d;i<len;i++){
				int temp = arr[i];
				int j=i-d;
				for(;j>=0;j=j-d){
					if(arr[j]<=temp){
						break;
					}else{
						arr[j+d]=arr[j];
					}
				}
				arr[j+d]=temp;
			}
			d = d/2;
		}
	}

        6、归并排序

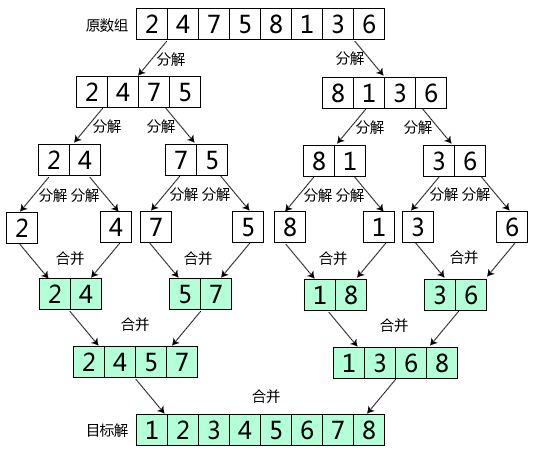
       归并排序先将数组拆成一个一个数，每个数认为是一个有序表，然后将相邻两个有序表合并成一个有序表，依次两两合并直到只剩一个有序表。一般采用递归形式编写。两个有序表合并成一个有序表的过程中一般需要使用额外空间，因此空间复杂度为O(n)，因此上表这处有误。

        图片来源http://www.cnblogs.com/horizonice/p/4102553.html

	public static void myMergeSort(int[] arr, int st, int fh){
		if(st>=fh){
			return;//已经拆成一个数字
		}else{
			int mid = (st+fh)/2;
			myMergeSort(arr, st, mid);
			myMergeSort(arr, mid+1, fh);
			Merge(arr, st, mid, fh);//将两个有序表arr[st:mid]和arr[mid+1:fh]合并成一个
		}
	}

	static int[] temp = new int[arr.length];
	public static void Merge(int[] arr, int st, int mid, int fh){
		int i = st;    //两个指针指向两个子有序表的开头
		int j = mid+1;
		int k = 0;
		while(i<=mid&&j<=fh){
			if(arr[i]<=arr[j]){
				temp[k] = arr[i];
				i++;
				k++;
			}else{
				temp[k] = arr[j];
				j++;
				k++;
			}
		}

		while(i<=mid){
			temp[k] = arr[i];
			i++;
			k++;
		}
		while(j<=fh){
			temp[k] = arr[j];
			j++;
			k++;
		}

		for(int n=0;n<k;n++){
			arr[st+n] = temp[n];
		}
	}

        7、堆排序

        堆排序是利用堆这种数据结构进行排序的算法。堆这种数据结构是一种特殊的完全二叉树，最大堆要求每个节点的值都不大于其父节点的值；反之，最小堆要求每个节点的值都不小于其父节点的值。

        堆排序详细内容见：http://www.cnblogs.com/mengdd/archive/2012/11/30/2796845.html，讲的很好。

public class HeapSort{
	private static int[] sort=new int[]{1,0,10,20,3,5,6,4,9,8,12,17,34,11};

	public static void main(String[] args){
		buildMaxHeapify(sort);
		heapSort(sort);
		print(sort);
	}

	private static void buildMaxHeapify(int[] data){
		//没有子节点的才需要创建最大堆，从最后一个的父节点开始
		int startIndex=getParentIndex(data.length-1);
		//从尾端开始创建最大堆，每次都是正确的堆
		for(int i=startIndex;i>=0;i--){
			maxHeapify(data,data.length,i);
		}
	}

	/**
	*创建最大堆
	*
	*@paramdata
	*@paramheapSize需要创建最大堆的大小，一般在sort的时候用到，因为最多值放在末尾，末尾就不再归入最大堆了
	*@paramindex当前需要创建最大堆的位置
	*/
	private static void maxHeapify(int[] data,int heapSize,int index){
		//当前点与左右子节点比较
		int left=getChildLeftIndex(index);
		int right=getChildRightIndex(index);

		int largest=index;
		if(left<heapSize&&data[index]<data[left]){
			largest=left;
		}
		if(right<heapSize&&data[largest]<data[right]){
			largest=right;
		}
		//得到最大值后可能需要交换，如果交换了，其子节点可能就不是最大堆了，需要重新调整
		if(largest!=index){
			int temp=data[index];
			data[index]=data[largest];
			data[largest]=temp;
			maxHeapify(data,heapSize,largest);
		}
	}

	/**
	*排序，最大值放在末尾，data虽然是最大堆，在排序后就成了递增的
	*
	*@paramdata
	*/
	private static void heapSort(int[] data){
		//末尾与头交换，交换后调整最大堆
		for(int i=data.length-1;i>0;i--){
			int temp=data[0];
			data[0]=data[i];
			data[i]=temp;
			maxHeapify(data,i,0);
		}
	}

	/**
	*父节点位置
	*
	*@paramcurrent
	*@return
	*/
	private static int getParentIndex(int current){
		return(current-1)>>1;
	}

	/**
	*左子节点position注意括号，加法优先级更高
	*
	*@paramcurrent
	*@return
	*/
	private static int getChildLeftIndex(int current){
		return(current<<1)+1;
	}

	/**
	*右子节点position
	*
	*@paramcurrent
	*@return
	*/
	private static int getChildRightIndex(int current){
		return(current<<1)+2;
	}

	private static void print(int[] data){
		int pre=-2;
		for(int i=0;i<data.length;i++){
			if(pre<(int)getLog(i+1)){
				pre=(int)getLog(i+1);
				System.out.println();
			}
			System.out.print(data[i]+"|");
		}
	}

	/**
	*以2为底的对数
	*
	*@paramparam
	*@return
	*/
	private static double getLog(double param){
		return Math.log(param)/Math.log(2);
	}
}