-
堆中某个节点的值总是不大于或不小于其父节点的值;
-
堆总是一棵完全树。
支持的基本操作
-
build:建立一个空堆;
-
insert:向堆中插入一个新元素;
-
update:将新元素提升使其符合堆的性质;
-
get:获取当前堆顶元素的值;
-
delete:删除堆顶元素;
-
heapify:使删除堆顶元素的堆再次成为堆。
算法思想
#include <iostream>
using namespace std;
template<class T>
class MinHeap
{
private:
T *heap; //元素数组,0号位置也储存元素
int CurrentSize; //目前元素个数
int MaxSize; //可容纳的最多元素个数
void FilterDown(const int start,const int end); //自上往下调整,使关键字小的节点在上
void FilterUp(int start); //自下往上调整
public:
MinHeap(int n=1000);
~MinHeap();
bool Insert(const T &x); //插入元素
T RemoveMin(); //删除最小元素
T GetMin(); //取最小元素
bool IsEmpty() const;
bool IsFull() const;
void Clear();
};
template<class T>
MinHeap<T>::MinHeap(int n)
{
MaxSize=n;
heap=new T[MaxSize];
CurrentSize=0;
}
template<class T>
MinHeap<T>::~MinHeap()
{
delete []heap;
}
template<class T>
void MinHeap<T>::FilterUp(int start) //自下往上调整
{
int j=start,i=(j-1)/2; //i指向j的双亲节点
T temp=heap[j];
while(j>0)
{
if(heap[i]<=temp)
break;
else
{
heap[j]=heap[i];
j=i;
i=(i-1)/2;
}
}
heap[j]=temp;
}
template<class T>
void MinHeap<T>::FilterDown(const int start,const int end) //自上往下调整,使关键字小的节点在上
{
int i=start,j=2*i+1;
T temp=heap[i];
while(j<=end)
{
if( (j<end) && (heap[j]>heap[j+1]) )
j++;
if(temp<=heap[j])
break;
else
{
heap[i]=heap[j];
i=j;
j=2*j+1;
}
}
heap[i]=temp;
}
template<class T>
bool MinHeap<T>::Insert(const T &x)
{
if(CurrentSize==MaxSize)
return false;
heap[CurrentSize]=x;
FilterUp(CurrentSize);
CurrentSize++;
return true;
}
template<class T>
T MinHeap<T>::RemoveMin( )
{
T x=heap[0];
heap[0]=heap[CurrentSize-1];
CurrentSize--;
FilterDown(0,CurrentSize-1); //调整新的根节点
return x;
}
template<class T>
T MinHeap<T>::GetMin()
{
return heap[0];
}
template<class T>
bool MinHeap<T>::IsEmpty() const
{
return CurrentSize==0;
}
template<class T>
bool MinHeap<T>::IsFull() const
{
return CurrentSize==MaxSize;
}
template<class T>
void MinHeap<T>::Clear()
{
CurrentSize=0;
}
//最小堆:根结点的键值是所有堆结点键值中最小者。
int main ()
{
int k,n=11,a[11]={0,5,2,4,9,7,3,1,10,8,6};
MinHeap<int> test(11);
for(k=0; k<n; k++)
test.Insert(a[k]);
cout<<test.IsFull()<<endl;
for(k=0;k<n;k++)
cout<<test.RemoveMin()<<ends;
cout<<endl;
return 0;
}#include <stdio.h>
#include <math.h>
inline void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// array是待调整的堆数组,i是待调整的数组元素的位置,nlength是数组的长度
//本函数功能是:根据数组array构建大根堆
void MaxHeapFixdown(int array[], int i, int nLength)
{
int temp = array[i];
// 子结点的位置=2*(父结点位置)+ 1
int j = 2 * i + 1;
while ( j < nLength ) {
// 得到子结点中较大的结点
if ( j < nLength - 1 && array[j] < array[j + 1]) {
++ j;
}
// 否则退出循环
if (temp > array[j]) {
break;
}
// 如果较大的子结点大于父结点那么把较大的子结点往上移动,替换它的父结点
array[i] = array[j];
i = j;
// 子结点的位置=2*(父结点位置)+ 1
j = 2 * i + 1;
}
// 最后把需要调整的元素值放到合适的位置
array[i] = temp;
}
//array是待调整的堆数组,i是待调整的数组元素的位置,nlength是数组的长度
//从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
//本函数功能是:根据数组array构建小根堆
void MinHeapFixdown(int a[], int i, int n)
{
int temp = a[i];
int j = 2 * i + 1;
while (j < n) {
//在左右孩子中找最小的
if (j < n - 1 && a[j + 1] < a[j]) {
++ j;
}
if (a[j] >= temp) {
break;
}
//把较小的子结点往上移动,替换它的父结点
a[i] = a[j];
i = j;
j = 2 * i + 1;
}
a[i] = temp;
}
// 堆排序算法
void HeapSort(int array[],int length)
{
int i;
// 调整序列的前半部分元素,调整完之后第一个元素是序列的最大的元素
//length/2-1是第一个非叶节点,此处"/"为整除
for ( i = length / 2 - 1; i >= 0; -- i) {
MaxHeapFixdown(array, i, length);
}
// 从最后一个元素开始对序列进行调整,不断的缩小调整的范围直到第一个元素
for ( i = length - 1; i > 0; -- i) {
// 把第一个元素和当前的最后一个元素交换,
// 保证当前的最后一个位置的元素都是在现在的这个序列之中最大的
swap(&array[0], &array[i]);
// 不断缩小调整heap的范围,每一次调整完毕保证第一个元素是当前序列的最大值
MaxHeapFixdown(array, 0, i);
}
}
double Sqrt(double number)
{
if(number<=0)return 0;
//设置初始值i,i值越接近sqrt(number),所需循环次数越少
double i = 1; //一个快速算法是:int exp;double i=ldexp(frexp(number,&exp),(exp>>1));
double j = number/i;
while((i<j?j-i:i-j) > 1e-9)//随着循环次数的增加,i与j将非常接近
{
i = (i+j)/2;
j = number/i ;
}
return i;
}
int main()
{
/*
int a[] = {10,1,3,5,111,7,9,0,8,6,4,2,100,11};
const int len = sizeof (a) / sizeof(int);
HeapSort(a, len);
for (int i = 0 ; i < len; ++ i)
{
printf("%d ", a[i]);
}
*/
const double N = 144;
printf ("sqrt(%f) = %f\n",N ,Sqrt(N));
return 0;
}
二叉堆的定义
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:
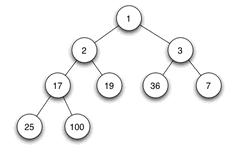
由于其它几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就简称为堆。
堆的存储
一般都用数组来表示堆,i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

堆的操作——插入删除
下面先给出《数据结构C++语言描述》中最小堆的建立插入删除的图解,再给出本人的实现代码,最好是先看明白图后再去看代码。
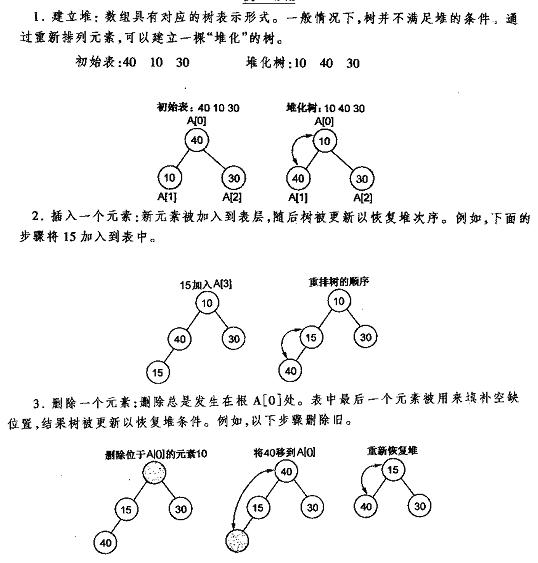
堆的插入
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列,现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中,对照《白话经典算法系列之二 直接插入排序的三种实现》不难写出插入一个新数据时堆的调整代码:
- // 新加入i结点 其父结点为(i - 1) / 2
- void MinHeapFixup(int a[], int i)
- {
- int j, temp;
- temp = a[i];
- j = (i - 1) / 2; //父结点
- while (j >= 0 && i != 0)
- {
- if (a[j] <= temp)
- break;
- a[i] = a[j]; //把较大的子结点往下移动,替换它的子结点
- i = j;
- j = (i - 1) / 2;
- }
- a[i] = temp;
- }
更简短的表达为:
- void MinHeapFixup(int a[], int i)
- {
- for (int j = (i - 1) / 2; (j >= 0 && i != 0)&& a[i] > a[j]; i = j, j = (i - 1) / 2)
- Swap(a[i], a[j]);
- }
插入时:
- //在最小堆中加入新的数据nNum
- void MinHeapAddNumber(int a[], int n, int nNum)
- {
- a[n] = nNum;
- MinHeapFixup(a, n);
- }
堆的删除
按定义,堆中每次都只能删除第0个数据。为了便于重建堆,实际的操作是将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码:
- // 从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
- void MinHeapFixdown(int a[], int i, int n)
- {
- int j, temp;
- temp = a[i];
- j = 2 * i + 1;
- while (j < n)
- {
- if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
- j++;
- if (a[j] >= temp)
- break;
- a[i] = a[j]; //把较小的子结点往上移动,替换它的父结点
- i = j;
- j = 2 * i + 1;
- }
- a[i] = temp;
- }
- //在最小堆中删除数
- void MinHeapDeleteNumber(int a[], int n)
- {
- Swap(a[0], a[n - 1]);
- MinHeapFixdown(a, 0, n - 1);
- }
堆化数组
有了堆的插入和删除后,再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧,不用!先看一个数组,如下图:
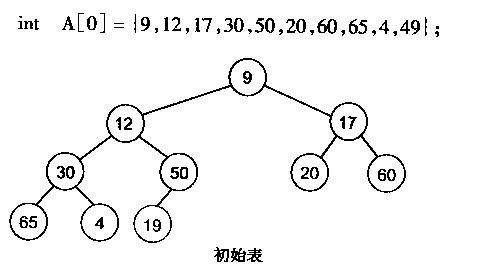
很明显,对叶子结点来说,可以认为它已经是一个合法的堆了即20,60, 65, 4, 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30,A[2] = 17,A[1] = 12,A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤:
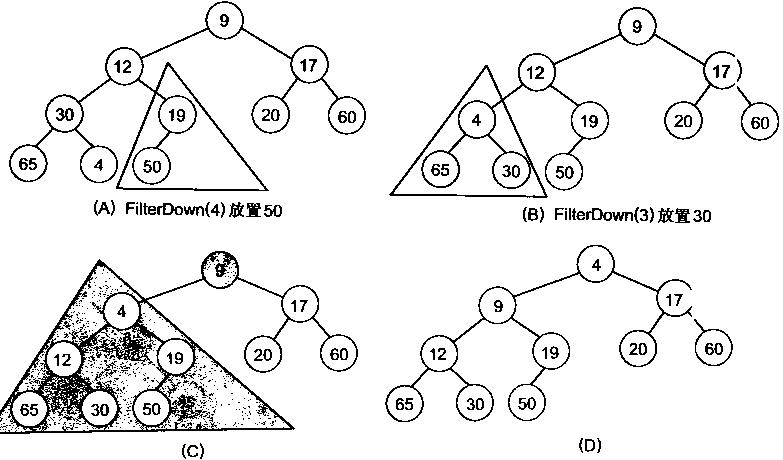
写出堆化数组的代码:
- //建立最小堆
- void MakeMinHeap(int a[], int n)
- {
- for (int i = n / 2 - 1; i >= 0; i--)
- MinHeapFixdown(a, i, n);
- }
至此,堆的操作就全部完成了(注1),再来看下如何用堆这种数据结构来进行排序。
堆排序
首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据,重复上述步骤直至堆中只有一个数据时就直接取出这个数据。
由于堆也是用数组模拟的,故堆化数组后,第一次将A[0]与A[n - 1]交换,再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换,再对A[0…n - 3]重新恢复堆,重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间,故操作完成后整个数组就有序了。有点类似于直接选择排序。
- void MinheapsortTodescendarray(int a[], int n)
- {
- for (int i = n - 1; i >= 1; i--)
- {
- Swap(a[i], a[0]);
- MinHeapFixdown(a, 0, i);
- }
- }
注意使用最小堆排序后是递减数组,要得到递增数组,可以使用最大堆。
由于每次重新恢复堆的时间复杂度为O(logN),共N - 1次重新恢复堆操作,再加上前面建立堆时N / 2次向下调整,每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。STL也实现了堆的相关函数,可以参阅《STL系列之四 heap 堆》。
注1 作为一个数据结构,最好用类将其数据和方法封装起来,这样即便于操作,也便于理解。此外,除了堆排序要使用堆,另外还有很多场合可以使用堆来方便和高效的处理数据,以后会一一介绍。
上文补充部分摘自:http://blog.csdn.net/morewindows/article/details/6709644






















 24万+
24万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








