AC算法是Alfred V.Aho(《编译原理》(龙书)的作者),和Margaret J.Corasick于1974年提出(与KMP算法同年)的一个经典的多模式匹配算法,可以保证对于给定的长度为n的文本,和模式集合P{p1,p2,...pm},在O(n)时间复杂度内,找到文本中的所有目标模式,而与模式集合的规模m无关。正如KMP算法在单模式匹配方面的突出贡献一样,AC算法对于多模式匹配算法后续的发展也产生了深远的影响,而且更为重要的是,两者都是在对同一问题——模式串前缀的自包含问题的研究中,产生出来的,AC算法从某种程度上可以说是KMP算法在多模式环境下的扩展。在我的《KMP算法详解》一文中,我在最后已经提到,如果要用KMP算法匹配长度为n的文本中的m个模式,则需要为每一个模式维护一个next跳转表,在执行对文本的匹配过程中,我们需要关注所有这些next表的状态转移情况,这使得时间复杂度增长为O(mn),对于较大的模式集合来说,这样的时间增长可能是无法接受的。AC算法解决了这一问题,通过对模式集合P的预处理,去除了模式集合的规模对匹配算法速度的影响。
要理解AC算法,仍然需要对KMP算法的透彻理解。这里我们还是以KMP算法中的老例子来说明前缀自包含如何在AC算法中发挥作用。对于模式串"abcabcacab",我们知道非前缀子串abc(abca)cab是模式串的一个前缀(abca)bcacab,而非前缀子串ab(cabca)cab不是模式串abcabcacab的前缀,根据此点,我们构造了next结构,实现在匹配失败时的跳转。而对于多模式环境,这个情况会发生一定的变化。这里以AC论文中的例子加以说明,对于模式集合P{he,she,his,hers},模式s(he)的非前缀子串he,实际上却是模式(he),(he)rs的前缀。如果目标串target[i...i+2]与模式she匹配,同时也意味着target[i+1...i+2]与he,hers这两个模式的头两个字符匹配,所以此时对于target[i+3],我们不需要回溯目标串的当前位置,而直接将其与he,hers两个模式的第3个字符对齐,然后直接向后继续执行匹配操作。
经典的AC算法由三部分构成,goto表,fail表和output表,goto表是由模式集合P中的所有模式构成的状态转移自动机,以上面的集合为例,其对应的goto结果如下,其中圆圈对应自动机的各个状态,边对应当前状态输入的字符。
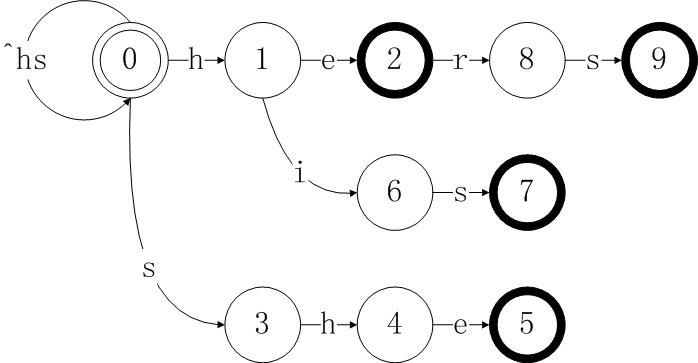
对于给定的集合P{p1,p2,...pm},构建goto表的步骤是,对于P中的每一个模式pi[1...j](1<=i<m+1),按照其包含的字母从前到后依次输入自动机,起始状态D[0],如果自动机的当前状态D[p],对于pi中的当前字母pi[k](1<=k<=j),没有可用的转移,则将状态机的总状态数smax+1,并将当前状态输入pi[k]后的转移位置,置为D[p][pi[k]] = smax,如果存在可用的转移方案D[p][pi[k]]=q,则转移到状态D[q],同时取出模式串的下一个字母pi[k+1],继续进行上面的判断过程。这里我们所说的没有可用的转移方案,等同于转移到状态机D的初始状态D[0],即对于自动机状态D[p],输入字符pi[k],有D[p][pi[k]]=0。理论介绍很繁琐,让我们以之前的模式集合P{he,she,his,hers}说明一下goto表的构建过程。
第一步,将模式he加入goto表:
![]()
第二步,将模式she加入goto表:

第三步,将模式his加入goto表:
第四步,将模式hers加入goto表:
对于第一和第二步而言,两个模式没有重叠的前缀部分,所以每输入一个字符,都对应一个新状态。第三步时,我们发现,D[0][p3[1]]=D[0]['h']=1,所以对于新模式p3的首字母'h',我们不需要新增加一个状态,而只需将D的当前状态转移到D[1]即可。而对于模式p4其前两个字符he使状态机转移至状态D[2],所以其第三字符对应的状态D[8]就紧跟在D[2]之后。
goto表构建完成之后,我们就要构建fail表,所谓的fail表就是当我们处在状态机的某个状态D[p]时,此时的输入字符c使得D[p][c]=0,那么我们应该转移到状态机的哪个位置来继续进行呢。以输入文本"shers"为例,当输入到字母e时,我们会发现匹配模式(she)rs,对应与状态机的状态D[5],然后输入字母r,此时我们发现D[6]['r']=0,对于字母r D[6]不存在有意义的跳转。此时我们不能跳转回状态D[0],这样就会丢掉可能的匹配s(hers)。我们发现s(he)的后缀he是模式(he)rs的一个前缀,所以当匹配模式she时,实际也已经匹配了模式hers的前缀he,此时我们可以将状态D[6]转移到hers中的前缀he在goto表中的对应状态D[2]处,再向后执行跳转匹配。这一跳转,就是AC算法中的fail跳转,要实现正确的fail跳转,还需要满足一系列条件,下面会逐一说明。
对于模式串she,其在字母e之后发生了匹配失败,此时其对应的模式串(回溯到状态D[0])就是she。对于she来说,它有两个包含后缀(除字符串自身外的所有后缀),he和e,对于后缀he,将其输入自动机D,从状态D[0]可以转移到状态D[2],对于后缀e,没有可行的状态转移方案。所以对于状态D[5],如果对于新输入的字符c没有可行的转移方案,我们可以跳转到状态D[2],考察D[2][c]是否等于0.
AC两人在论文中举出的例子,并不能涵盖在构建fail时遇到的所有情况,这里特别说明一下。前面我们说过,对于she的包含后缀e,没有可行的转移方案,此时如果模式串中还包含一个模式era,那么D[5]可不可以转移到状态D[10]去呢,实际上这是不行的,我们需要找到的是当前所有包含后缀中最长的满足条件者(拗口),如果D[5]对于失败的输入c优先转移到D[10],那么对于文本串shers,很显然会漏掉可能匹配hers,那么什么时机才应该转移到D[10]呢,当我们处理模式串hers时,处理到D[2]时对于之前的输入he,其最长的包含后缀是e,将e输入自动机,可以转移到D[10],所以在D[2]处发生匹配失败的时候才应该转移到D[10]。所以当我们在D[5]处匹配失败时,要先跳转到D[2]如果再没有可用的转移,再跳转到D[10]。

这个例子同时说明,对于模式集合P的所有模式pi,我们需要处理的不仅是pi的所有包含后缀,而是pi的所有非前缀子串。以模式hers为例,其在2,8,9三个状态都可能发生匹配失败,所以我们要提取出hers的所有非前缀子串(e,er,r,ers,rs,s),然后按照这些子串的末尾字符所对应的自动机状态分组(上例就可以分组为{e}对应状态2,{er,r}对应状态8,{ers,rs,s}对应状态9),然后分别将这些组中的子串从D[0]开始执行状态转移,直到没有可行的转移方案,或者整个序列使状态机最终转移到一个合法状态为止。如果一组中的所有子串都不能使状态机转移到一个合法状态,则这组子串所对应的状态的fail值为0,如果存在可行的状态转移方案,则选择其中最长的子串经过转移后的最终状态,令其对应的组的状态的fail值与其相等。
举例说明,当我们要处理模式串hers的fail表,假设已经构建好的goto表如前图所示,首先我们需要考察状态2,此时hers的输入字符是he,其所有包含后缀只有e,我们让e从D[0]开始转移,发现成功转移到D[10],所以fail[2]=10。然后我们考察状态8,此时hers的输入字符是her,所有包含后缀为er,r,因为我们要找到可以实现转移的最大包含后缀,所以我们先让er从D[0]开始转移,发现成功转移到D[11],所以fail[8]=11,这是虽然后缀e也可以成功转移到D[10],但是不是当前包含后缀分组中的子串所能实现的最长跳转,放弃。然后我们考察9,此时hers的输入字符串是hers,所有包含后缀为ers,rs,s,我们依次让其执行状态转换,发现s是可以实现转移的最长子串,转移到D[3],所以fail[9]=3。
我在《KMP算法详解》一文中讲到过一个找当前位置最大包含前缀的笨方法,现在我们构建fail表的方法,就是那一方法在多模式环境下的重新演绎。对于长度为n的模式串p而言,其所有非前缀子串的总数有(n^2-n)/2个,如果将这些子串都要经过状态机执行状态转移,时间复杂度为O(n^3),所以用这种方法,计算包含m个模式的模式集合P的fail表的时间复杂度为O(mn^3),如果包含10000个模式,模式的平均长度为10,计算fail表的运算就是千万级别,严重影响AC算法的实用价值。不过还好Aho,Corasick在自己的论文中同时给出了一个与模式串总长度相关的线性时间算法,可以参考我的这篇文章,但是这个方法的正确性不那么显而易见。不过这并非就意味着蛮力法就没有什么价值了,蛮力法一方面容易理解,可以为我们探索更高效的算法提供灵感,另一方面也可以帮助我们验证高效算法的正确性。
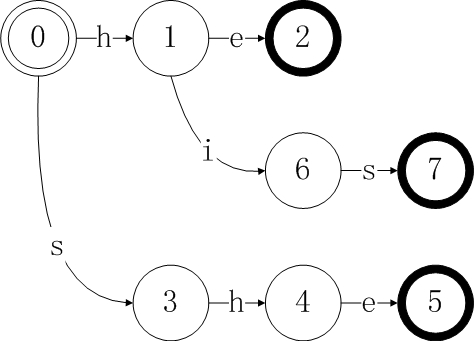
最后我们来说一下AC算法中的output表,在构建goto表的过程中,我们知道,状态2,5,7,9是输入的4个模式串的末尾部分,所以如果在执行匹配过程中,达到了如下四个状态,我们就知道对应的模式串被发现了。对于状态机D的某些状态,对应某个完整的模式串已经被发现,我们就用output表来记录这一信息。完成goto表的构建后,D中各状态对应的output表的情况如下:
2 he
5 she
7 his
9 hers
但是这并不是我们最终的output表。下面以构建状态5的fail表为例,说明一下fail表的构建是如何影响output表的。首先根据之前我们的介绍,当我们开始计算D[5]的fail值时,我们要将模式she的所有包含后缀提取出来,包括he,e。这里我们需要注意,在output表中,状态5是一个输出状态。当我们用he在状态机中执行转移时,我们会成功转移到2,这里output[2]也是一个输出状态,这就意味着在发现模式串she的同时,实际上也发现了模式串he,所以如果通过某种转换,我们到达了状态5,则意味着我们发现了she和he两个模式,此时fail[5]=2,所以我们需要将output[2]所包含的输出字符串加入到output[5]中。完成goto和fail表构建后,我们所得到的最终output表为:
2 he
5 she,he
7 his
9 hers
这实际上是一个后缀包含问题,也就是模式p1实际上是模式p2的后缀,所以当发现模式p2时,p1自然也被发现了。
AC算法对文本进行匹配的具体步骤是。一开始,将i指向文本text[1...j]的起始位置,然后用text[i]从goto表的状态D[0]开始执行状态跳转。如果存在可行的跳转方案D[0][text[i]]=p,p!=0,则将i增加1,同时转移到状态D[p]。如果不存在可行的转移方案,则考察状态D[p]的fail值,如果fail[p]不等于0,则转移到D[fail[p]],再次查看D[fail[p]][text[i]]是否等于0,直到发现不为0的状态转移方案或者对于所有经历过的fail状态,对于当前输入text[i]都没有非0的转移方案为止,如果确实不存在非0的转移方案,则将i增加1,同时转移到D[0]继续执行跳转。在每次跳转到一个状态D[p]时(fail跳转不算),都需要查看一下output[p]是否指向可输出的模式串,如果有,说明当前位置匹配了某些模式串,将这些模式串输出。
下面就是一个AC算法的简单示例,由于是示例程序,重在演示实现,所以做了一些简化,这里假设输入字符只包含小写英文字母(26个)。我用了一个二维数组来保存goto表信息,这样可以实现比较直接的跳转,缺点是浪费大量的内存空间。AC算法中goto表状态的数量,可以参考模式中所有的字符数,所以对于上万模式的应用场景,内存空间的占用会很惊人,如何既能存储如此多的状态,又能实现低成本的状态跳转,是一个需要研究的问题,后续我还会专门撰文介绍。
首先是程序中用到的goto,fail,output表结构和几个宏定义。
- #define ALPHABET_SIZE 26
- #define MAXIUM_STATES 100
- int _goto[MAXIUM_STATES][ALPHABET_SIZE];
- int _fail[MAXIUM_STATES];
- set<string> _out[MAXIUM_STATES];//使用set是因为在生成fail表,同时更新out表过程中,有可能向同一位置多次插入同一个模式串
然后是计算goto表的算法。
- inline void BuildGoto(const vector<string>& patterns)
- {
- unsigned int used_states;
- unsigned int t;
- vector<string>::const_iterator vit;
- string::const_iterator sit;
- for(vit = patterns.begin(), used_states = 0; vit != patterns.end(); ++vit)
- {
- for(sit = vit->begin(), t = 0; sit != vit->end(); ++sit)
- {
- if(_goto[t][(*sit)-'a'] == 0)
- {
- _goto[t][(*sit)-'a'] = ++used_states;
- t = used_states;
- }
- else
- {
- t = _goto[t][(*sit)-'a'];
- }
- }
- _out[t].insert(*vit);
- }
- }
然后是计算fail表的算法。
- inline void BuildFail(const vector<string>& patterns)
- {
- unsigned int t, m, last_state;
- unsigned int s[20];
- vector<string>::const_iterator vit;
- string::const_iterator sit1, sit2, sit3;
- for(vit = patterns.begin(); vit != patterns.end(); ++vit)
- {
- //先要找到输入的单词的各字母对应的状态转移表的状态号,由于状态转移表没有
- //记录各状态的前驱状态信息,该步暂时无法掠过
- t = 0;
- m = 0;
- sit1 = vit->begin();
- while(sit1 != vit->end() && _goto[t][*sit1 - 'a'] != 0)
- {
- t = _goto[t][*sit1 - 'a'];
- ++sit1;
- s[m++] = t;
- }
- for(sit1 = vit->begin() + 1; sit1 != vit->end(); ++sit1)
- {
- //此时的[sit2, sit1+1)就是当前模式的一个非前缀子串
- for(sit2 = vit->begin() + 1; sit2 != sit1 + 1; ++sit2)
- {
- t = 0;
- sit3 = sit2;
- //对该子串在goto表中执行状态转移
- while(sit3 != sit1 + 1 && _goto[t][*sit3 - 'a'] != 0)
- {
- t = _goto[t][*sit3 - 'a'];
- ++sit3;
- }
- //当前子串可以使goto表转移到一个非0位置
- if(sit3 == sit1 + 1)
- {
- //求出输入当前子串在goto表中所转移到的位置
- last_state = s[sit3-vit->begin() - 1];
- //更新该位置的fail值,如果改为值得fail值为0,则用t值替换,因为对于sit1而言,是按照以其为末尾元素的非前缀
- //子串的由长到短的顺寻在goto表中寻找非0状态转移的,而满足条件的t是这里免得最长子串
- if(_fail[last_state] == 0)
- {
- _fail[last_state] = t;
- }
- //如果两者都标识完整的模式串
- if(_out[last_state].size() > 0 && _out[t].size() > 0)
- {
- //将out[t]内的模式串全部加入out[last_state]中
- for(set<string>::const_iterator cit = _out[t].begin(); cit != _out[t].end(); ++cit)
- {
- _out[last_state].insert(*cit);
- }
- }
- }
- }
- }
- }
- }
然后是执行多模式匹配的AC算法。
- void AC(const string& text, const vector<string>& patterns)
- {
- unsigned int t = 0;
- string::const_iterator sit = text.begin();
- BuildGoto(patterns);
- BuildFail(patterns);
- //每次循环中,t都是*sit的前置状态
- while(sit != text.end())
- {
- //检查是否发现了匹配模式,如果有,将匹配输出
- if(_out[t].size() > 0)
- {
- cout << (sit - text.begin() - 1) << ": ";
- for(set<string>::const_iterator cit = _out[t].begin(); cit != _out[t].end(); ++cit)
- {
- cout << (*cit) << ", ";
- }
- cout << '\n';
- }
- if(_goto[t][*sit - 'a'] == 0)
- {
- t = _fail[t];
- //找到可以实现非0跳转的fail状态转移
- while(t != 0 && _goto[t][*sit - 'a'] == 0)
- {
- t = _fail[t];
- }
- if(t == 0)
- {
- //跳过那些在初始状态不能实现非0状态跳转的字母输入
- if(_goto[0][*sit - 'a'] == 0)
- {
- ++sit;
- }
- continue;
- }
- }
- t = _goto[t][*sit - 'a'];
- ++sit;
- }
- }
后记:
- KMP算法依然是解读AC算法的重要线索,前缀,子串,后缀永远和模式匹配纠缠在一起。
- AC状态机实际上更适合用Trie结构来存储。
- 可以将算法中使用到的goto,fail,output三张表以离线的方式计算出来保存在一个文件中,当AC算法启动时,直接从文件中读取三个表的内容,这样可以有效减少每次AC算法启动时都需要构建三个表所花费的时间。
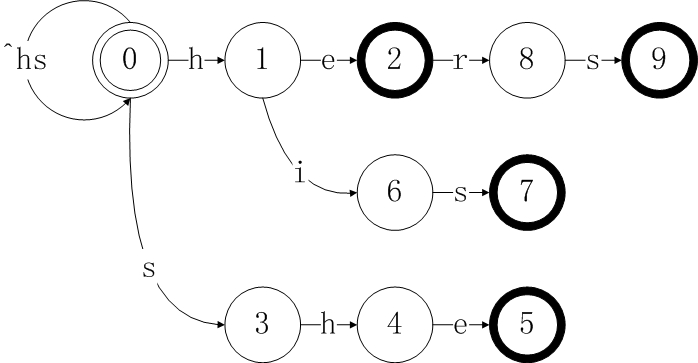
补充:上述一个很大的疏漏,那就是用蛮力法计算自动机的fail跳转表,这实际上是一个极度低效的方法。在Aho,Corasick两人的论文中,给出的是逐层求fail表的方法,两人证明了这个方法可以在O(n)(其中n为所有模式串的总长度和)时间复杂度内计算出模式集合P的fail跳转表,下面,我就来补完这一算法的执行步骤。还是以之前的模式集合P{he,she,his,hers,era}为例来说明,其构建的goto表如下图所示。这里为了描述方便,我们将该图简记为g,令g(a,b)为图中的一个转换a代表当前状态,b代表当前状态下的一个合法输入。例如g(1,e)=2表示节点1在输入字符e的情况下转换到节点2。

我们利用如下方法来求出g中所有节点的fail值。首先,令第1层节点的fail值都为0。然后,将第1层的节点依次加入队列queue尾部。然后,从队列queue的头部依次取出节点。对于取出的节点m,及其与子节点的状态转移g(m,i)=n,fail[n]的计算方法为,我们令fail[m]=p,如果p!=0且g(p,i)=0,我们令p=fail[p],直到p=0,或者g(p,i)!=0为止,此时fail[n]=g(p,i)。对于状态n,如果output[p]包含匹配的模式串,则将output[p]中的匹配的模式,全部加入output[n]中。如果节点n仍有子节点,则将节点n加入队列queue的尾部,直到队列queue中的所有节点处理完毕为止,我们就得到了除状态0之外的所有节点的fail值。下面举上图的三个例子说明。
1. fail[2]=g(fail[1],e)=g(0,e)=10,fail[6]=g(fail[1],i)=g(0,i)=0,这里对于第1层节点1,3,10,我们有fail[1]=0,fail[3]=0,fail[10]=0。
2. 对于fail[5],有g(4,e)=5,g(fail[4],e)=g(1,e)=2!=0,所以fail[5]=2,因为output[2]包含模式串he,所以我们要将output[2]中的内容添加到output[5]中,此时output[5]={she,he}。
3. 对于fail[9],我们有g(8,s)=9,g(fail[8],s)=g(11,s)=0,但是此时p=fail[8]!=0,所以我们接着考察fail[p]=fail[fail[8]]=fail[11]=0,此时fail[11]=0,g(fail[11],s)=g(0,s)=3,所以fail[9]的最终结果是3。由于节点3的output值为空,无需新增output[9]的内容。






















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








