Java面试宝典之二叉树的实现

最新推荐文章于 2023-07-08 00:00:00 发布
最新推荐文章于 2023-07-08 00:00:00 发布
阅读量698 收藏 1
点赞数
分类专栏： java 文章标签： Java 面试题 数据结构 二叉树

我们接着上一篇数据结构继续讲解。本章系数据结构之树与二叉树，从这章开始，我们就要介绍非线性结构了，这些内容理解起来比线性表稍难一些，我尽量写的通俗一些，如果读的过程中有任何问题，请按上述方式联系我！

一、树

树形结构是一类重要的非线性结构。树形结构是结点之间有分支，并具有层次关系的结构。它非常类似于自然界中的树。树结构在客观世界中是大量存在的，例如家谱、行政组织机构都可用树形象地表示。树在计算机领域中也有着广泛的应用，例如在编译程序中，用树来表示源程序的语法结构；在数据库系统中，可用树来组织信息；在分析算法的行为时，可用树来描述其执行过程。本章重点讨论二叉树的存储表示及其各种运算，并研究一般树和森林与二叉树的转换关系，最后介绍树的应用实例。

二、二叉树

二叉树(BinaryTree)是n(n≥0)个结点的有限集，它或者是空集(n=0)，或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。关于更多概念，请大家自己上网查询，我们这里将用代码实现常见的算法。更多的概念，请访问：http://student.zjzk.cn/course_ware/data_structure/web/SHU/shu6.2.3.1.htm 。

1、二叉树的建立

首先，我们采用广义表建立二叉树（关于广义表的概念，请查看百科的介绍：http://baike.baidu.com/view/203611.htm）

我们建立一个字符串类型的广义表作为输入：

String  expression = "A(B(D(,G)),C(E,F))";与该广义表对应的二叉树为：


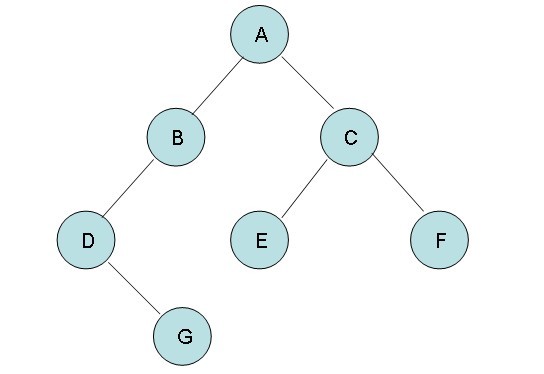
写代码前，我们通过观察二叉树和广义表，先得出一些结论：

  • 每当遇到字母，将要创建节点
  • 每当遇到“（”，表面要创建左孩子节点
  • 每当遇到“，”，表明要创建又孩子节点
  • 每当遇到“）”，表明要返回上一层节点
  • 广义表中“（”的数量正好是二叉树的层数

根据这些结论，我们基本就可以开始写代码了。首先建议一个节点类（这也属于一种自定义的数据结构）。

[java] view plain copy print ?
  1. package com.xtfggef.algo.tree;  
  2.   
  3. public class Node {  
  4.   
  5.     private char data;  
  6.     private Node lchild;  
  7.     private Node rchild;  
  8.   
  9.     public Node(){  
  10.           
  11.     }  
  12.     public char getData() {  
  13.         return data;  
  14.     }  
  15.   
  16.     public void setData(char data) {  
  17.         this.data = data;  
  18.     }  
  19.   
  20.     public Node getRchild() {  
  21.         return rchild;  
  22.     }  
  23.   
  24.     public void setRchild(Node rchild) {  
  25.         this.rchild = rchild;  
  26.     }  
  27.   
  28.     public Node getLchild() {  
  29.         return lchild;  
  30.     }  
  31.   
  32.     public void setLchild(Node lchild) {  
  33.         this.lchild = lchild;  
  34.     }  
  35.   
  36.     public Node(char ch, Node rchild, Node lchild) {  
  37.         this.data = ch;  
  38.         this.rchild = rchild;  
  39.         this.lchild = lchild;  
  40.     }  
  41.   
  42.     public String toString() {  
  43.         return "" + getData();  
  44.     }  
  45. }  
package com.xtfggef.algo.tree;

public class Node {

	private char data;
	private Node lchild;
	private Node rchild;

	public Node(){
		
	}
	public char getData() {
		return data;
	}

	public void setData(char data) {
		this.data = data;
	}

	public Node getRchild() {
		return rchild;
	}

	public void setRchild(Node rchild) {
		this.rchild = rchild;
	}

	public Node getLchild() {
		return lchild;
	}

	public void setLchild(Node lchild) {
		this.lchild = lchild;
	}

	public Node(char ch, Node rchild, Node lchild) {
		this.data = ch;
		this.rchild = rchild;
		this.lchild = lchild;
	}

	public String toString() {
		return "" + getData();
	}
}
根据广义表创建二叉树的代码如下：

[java] view plain copy print ?
  1. public Node createTree(String exp) {  
  2.         Node[] nodes = new Node[3];  
  3.         Node b, p = null;  
  4.         int top = -1, k = 0, j = 0;  
  5.         char[] exps = exp.toCharArray();  
  6.         char data = exps[j];  
  7.         b = null;  
  8.         while (j < exps.length - 1) {  
  9.             switch (data) {  
  10.             case '(':  
  11.                 top++;  
  12.                 nodes[top] = p;  
  13.                 k = 1;  
  14.                 break;  
  15.             case ')':  
  16.                 top--;  
  17.                 break;  
  18.             case ',':  
  19.                 k = 2;  
  20.                 break;  
  21.             default:  
  22.                 p = new Node(data, null, null);  
  23.                 if (b == null) {  
  24.                     b = p;  
  25.                 } else {  
  26.                     switch (k) {  
  27.                     case 1:  
  28.                         nodes[top].setLchild(p);  
  29.                         break;  
  30.                     case 2:  
  31.                         nodes[top].setRchild(p);  
  32.                         break;  
  33.                     }  
  34.                 }  
  35.             }  
  36.             j++;  
  37.             data = exps[j];  
  38.         }  
  39.         return b;  
  40.     }  
public Node createTree(String exp) {
		Node[] nodes = new Node[3];
		Node b, p = null;
		int top = -1, k = 0, j = 0;
		char[] exps = exp.toCharArray();
		char data = exps[j];
		b = null;
		while (j < exps.length - 1) {
			switch (data) {
			case '(':
				top++;
				nodes[top] = p;
				k = 1;
				break;
			case ')':
				top--;
				break;
			case ',':
				k = 2;
				break;
			default:
				p = new Node(data, null, null);
				if (b == null) {
					b = p;
				} else {
					switch (k) {
					case 1:
						nodes[top].setLchild(p);
						break;
					case 2:
						nodes[top].setRchild(p);
						break;
					}
				}
			}
			j++;
			data = exps[j];
		}
		return b;
	}
思路不难，结合上述的理论，自己断点走一遍程序就懂了！

2、二叉树的递归遍历

二叉树的遍历有三种：先序、中序、后序，每种又分递归和非递归。递归程序理解起来有一定的难度，但是实现起来比较简单。对于上述二叉树，其：

    a 先序遍历

            A B D G C E F

    b 中序遍历

           D G B A E C F 

    c 后序遍历

           G D B E F C A

先、中、后序递归遍历如下：

[java] view plain copy print ?
  1. /** 
  2.      * pre order recursive 
  3.      *  
  4.      * @param node 
  5.      */  
  6.     public void PreOrder(Node node) {  
  7.         if (node == null) {  
  8.             return;  
  9.         } else {  
  10.             System.out.print(node.getData() + " ");  
  11.             PreOrder(node.getLchild());  
  12.             PreOrder(node.getRchild());  
  13.   
  14.         }  
  15.     }  
  16.   
  17.     /** 
  18.      * in order recursive 
  19.      *  
  20.      * @param node 
  21.      */  
  22.     public void InOrder(Node node) {  
  23.         if (node == null) {  
  24.             return;  
  25.         } else {  
  26.             InOrder(node.getLchild());  
  27.             System.out.print(node.getData() + " ");  
  28.             InOrder(node.getRchild());  
  29.         }  
  30.     }  
  31.   
  32.     /** 
  33.      * post order recursive 
  34.      *  
  35.      * @param node 
  36.      */  
  37.     public void PostOrder(Node node) {  
  38.         if (node == null) {  
  39.             return;  
  40.         } else {  
  41.             PostOrder(node.getLchild());  
  42.             PostOrder(node.getRchild());  
  43.             System.out.print(node.getData() + " ");  
  44.         }  
  45.     }  
/**
	 * pre order recursive
	 * 
	 * @param node
	 */
	public void PreOrder(Node node) {
		if (node == null) {
			return;
		} else {
			System.out.print(node.getData() + " ");
			PreOrder(node.getLchild());
			PreOrder(node.getRchild());

		}
	}

	/**
	 * in order recursive
	 * 
	 * @param node
	 */
	public void InOrder(Node node) {
		if (node == null) {
			return;
		} else {
			InOrder(node.getLchild());
			System.out.print(node.getData() + " ");
			InOrder(node.getRchild());
		}
	}

	/**
	 * post order recursive
	 * 
	 * @param node
	 */
	public void PostOrder(Node node) {
		if (node == null) {
			return;
		} else {
			PostOrder(node.getLchild());
			PostOrder(node.getRchild());
			System.out.print(node.getData() + " ");
		}
	}
二叉树的递归遍历实现起来很简单，关键是非递归遍历有些难度，请看下面的代码：

3、二叉树的非递归遍历

先序非递归遍历：

[java] view plain copy print ?
  1. public void PreOrderNoRecursive(Node node) {  
  2.         Node nodes[] = new Node[CAPACITY];  
  3.         Node p = null;  
  4.         int top = -1;  
  5.         if (node != null) {  
  6.             top++;  
  7.             nodes[top] = node;  
  8.             while (top > -1) {  
  9.                 p = nodes[top];  
  10.                 top--;  
  11.                 System.out.print(p.getData() + " ");  
  12.                 if (p.getRchild() != null) {  
  13.                     top++;  
  14.                     nodes[top] = p.getRchild();  
  15.                 }  
  16.                 if (p.getLchild() != null) {  
  17.                     top++;  
  18.                     nodes[top] = p.getLchild();  
  19.                 }  
  20.             }  
  21.         }  
  22.     }  
public void PreOrderNoRecursive(Node node) {
		Node nodes[] = new Node[CAPACITY];
		Node p = null;
		int top = -1;
		if (node != null) {
			top++;
			nodes[top] = node;
			while (top > -1) {
				p = nodes[top];
				top--;
				System.out.print(p.getData() + " ");
				if (p.getRchild() != null) {
					top++;
					nodes[top] = p.getRchild();
				}
				if (p.getLchild() != null) {
					top++;
					nodes[top] = p.getLchild();
				}
			}
		}
	}
原理：利用一个栈，先序遍历即为根先遍历，先将根入栈，然后出栈，凡是出栈的元素都打印值，入栈之前top++，出栈之后top--，利用栈后进先出的原理，右节点先于左节点进栈，根出栈后，开始处理左子树，然后是右子树，读者朋友们可以自己走一遍程序看看，也不算难理解！

中序非递归遍历：

[java] view plain copy print ?
  1. public void InOrderNoRecursive(Node node) {  
  2.         Node nodes[] = new Node[CAPACITY];  
  3.         Node p = null;  
  4.         int top = -1;  
  5.         if (node != null)  
  6.             p = node;  
  7.         while (p != null || top > -1) {  
  8.             while (p != null) {  
  9.                 top++;  
  10.                 nodes[top] = p;  
  11.                 p = p.getLchild();  
  12.             }  
  13.             if (top > -1) {  
  14.                 p = nodes[top];  
  15.                 top--;  
  16.                 System.out.print(p.getData() + " ");  
  17.                 p = p.getRchild();  
  18.             }  
  19.         }  
  20.     }  
public void InOrderNoRecursive(Node node) {
		Node nodes[] = new Node[CAPACITY];
		Node p = null;
		int top = -1;
		if (node != null)
			p = node;
		while (p != null || top > -1) {
			while (p != null) {
				top++;
				nodes[top] = p;
				p = p.getLchild();
			}
			if (top > -1) {
				p = nodes[top];
				top--;
				System.out.print(p.getData() + " ");
				p = p.getRchild();
			}
		}
	}
原理省略。

后续非递归遍历：

[java] view plain copy print ?
  1. public void PostOrderNoRecursive(Node node) {  
  2.         Node[] nodes = new Node[CAPACITY];  
  3.         Node p = null;  
  4.         int flag = 0, top = -1;  
  5.         if (node != null) {  
  6.             do {  
  7.                 while (node != null) {  
  8.                     top++;  
  9.                     nodes[top] = node;  
  10.                     node = node.getLchild();  
  11.                 }  
  12.                 p = null;  
  13.                 flag = 1;  
  14.                 while (top != -1 && flag != 0) {  
  15.                     node = nodes[top];  
  16.                     if (node.getRchild() == p) {  
  17.                         System.out.print(node.getData() + " ");  
  18.                         top--;  
  19.                         p = node;  
  20.                     } else {  
  21.                         node = node.getRchild();  
  22.                         flag = 0;  
  23.                     }  
  24.                 }  
  25.             } while (top != -1);  
  26.         }  
  27.     }  
public void PostOrderNoRecursive(Node node) {
		Node[] nodes = new Node[CAPACITY];
		Node p = null;
		int flag = 0, top = -1;
		if (node != null) {
			do {
				while (node != null) {
					top++;
					nodes[top] = node;
					node = node.getLchild();
				}
				p = null;
				flag = 1;
				while (top != -1 && flag != 0) {
					node = nodes[top];
					if (node.getRchild() == p) {
						System.out.print(node.getData() + " ");
						top--;
						p = node;
					} else {
						node = node.getRchild();
						flag = 0;
					}
				}
			} while (top != -1);
		}
	}

三、树与二叉树的转换

本人之前总结的：



这部分概念的其他知识，请读者自己上网查看。

吾爱瑾瑾
关注
  • 0
    点赞
  • 踩
  • 1
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
Java面试宝典-经典
03-28
5、说明生活中遇到的二叉树，用java实现二叉树 66 6、从类似如下的文本文件中读取出所有的姓名，并打印出重复的姓名和重复的次数，并按重复次数排序： 71 7、写一个Singleton出来。 75 8、递归算法题1 77 9、递归...
Java之美[从菜鸟到高手演变]之数据结构基础之树、二叉树
智慧演绎，无处不在
04-21 2万+
树在计算机领域中也有着广泛的应用，例如在编译程序中，用树来表示源程序的语法结构；原理：利用一个栈，先序遍历即为根先遍历，先将根入栈，然后出栈，凡是出栈的元素都打印值，入栈之前top++，出栈之后top--，利用栈后进先出的原理，右节点先于左节点进栈，根出栈后，开始处理左子树，然后是右子树，读者朋友们可以自己走一遍程序看看，也不算难理解！本章系数据结构之树与二叉树，从这章开始，我们就要介绍非线性结构了，这些内容理解起来比线性表稍难一些，我尽量写的通俗一些，如果读的过程中有任何问题，请按上述方式联系我！
二叉树（Java实现）
JiaXingNashishua的博客
05-22 1万+
声明：本文部分文章取自于 Java中关于二叉树详解_来学习的小张的博客-CSDN博客_java 二叉树原理 更多关于二叉树详情可以点击上面链接 一：树形结构 树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点： 有一个特殊的节点，称为根节点，根节点没有前驱节点； 除根节点外，其余节点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm，其中每一个
数据结构-树
coolingxyz的博客
11-20 407
树： 树的概念 树形结构是一类重要的非线性结构。树形结构是结点之间有分支，并具有层次关系的结构。它非常类似于自然界中的树。树结构在客观世界中是大量存在的，例如家谱、行政组织机构都可用树形象地表示。树在计算机领域中也有着广泛的应用，例如在编译程序中，用树来表示源程序的语法结构；在数据库系统中，可用树来组织信息；在分析算法的行为时，可用树来描述其执行过程。 二
【Java】二叉树
最新发布
qq_61635026的博客
07-08 1668
二叉树（Binary Tree）是一种常见的树形结构，它由节点（Node）和节点之间的关系构成。每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树中的每个节点可以为空（null）。
数据结构（二叉树）——Java实现
m0_56911284的博客
11-03 2658
认识二叉树，并用Java实现其一系列的操作。
Java面试宝典2010版
03-29
5、说明生活中遇到的二叉树，用java实现二叉树 66 6、从类似如下的文本文件中读取出所有的姓名，并打印出重复的姓名和重复的次数，并按重复次数排序： 71 7、写一个Singleton出来。 75 8、递归算法题1 77 9、递归...
Java 面试宝典
02-01
23、java 中实现多态的机制是什么？ ......................................................................... 17 24、abstract class 和 interface 有什么区别? ...............................................
Java面试宝典2012版
12-03
5、说明生活中遇到的二叉树，用java实现二叉树 66 6、从类似如下的文本文件中读取出所有的姓名，并打印出重复的姓名和重复的次数，并按重复次数排序： 71 7、写一个Singleton出来。 75 8、递归算法题1 77 9、...
Java面试 Java超级经典100问题 Java高级开发工程师必备 Java面试宝典
07-15
Java面试 Java超级经典100问题 Java高级开发工程师必备 Java面试宝典 1.赋值运算函数.2.单例设计模式.3.二维数组中查找目标值、4.替换字符串中的空格。5.从尾到头打印链表.6.由前序和中序遍历重建二叉树.7.用两个栈...
Java语言----二叉树
tq02的博客
05-28 2698
二叉树详细讲解，以及Java实现代码
Java二叉树
m0_64318128的博客
10-16 1656
二叉树的概念、性质、以及二叉树的基本操作
二叉树（Java版）
WYSCODER的博客
08-04 2728
二叉树，看这一篇就够了~~~
Java数据结构————二叉树
爱敲代码的三毛的博客
08-20 937
文章目录一、树型结构（了解）1.概念2. 树与非树3. 树的一些重要的概念4. 树的表示形式（了解）5. 树的一些应用二、二叉树1.二叉树的概念2.二叉树的基本形态3.两种特殊的二叉树4. 二叉树的性质5. 二叉树的存储三、二叉树的基本操作1.二叉树的遍历2.前序遍历3. 中序遍历4. 后序遍历5. 求结点个数6.求叶子结点个数7. 求第 k 层结点个数8.获取二叉树的高度9. 查找 val 所在结点10. 层序遍历11. 判断一棵树是不是完全二叉树完！ 要想了解二叉树先要知道什么是树 一、树型结构（..
Java的演变历程(发展史)
数据库
03-28 319
注：技术和语法只是其中的一部分，以影响程度作为选取描述优先顺。 Java语言的前身：Oak（橡树） Java1.0提出了“Write Once，Run Anywhere”的口号 JDK 1.1 技术：JAR文件格式、JDBC、JavaBeans、RMI。 语法：内部类（Inner Class）和反射（Reflection）。 JDK 1.2 把Java技术体系拆分为3个方向，分别是 ...
Java实现二叉树
热门推荐
oneTreeTallTall
07-03 2万+
二叉树的定义 树（tree）是一种抽象数据类型（ADT），用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点通过连接它们的边组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的树。 二叉树是一种特殊的树，每个节点最多只能有两个子节点。（如图1.1） 二叉搜索树要求：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的...
[数据结构]二叉树(JAVA)
weixin_53106294的博客
11-01 778
二叉树的基本概念及简单模拟实现
二叉树详解（Java）
weixin_45969711的博客
11-14 1349
也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。先访问左子节点，左子节点不为空就递归中序遍历，再访问根节点，然后再访问右子节点，右子节点不为空就递归中序遍历。先访问左子节点，左子节点不为空就递归后序遍历，再访问右子节点，右子节点不为空就递归后序遍历，然后再访问根节点。先访问根节点，再访问左节点，左节点不为空就递归前序遍历，再访问右节点，右节点不为空就递归前序遍历。若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=Log2(n+1)
java 二叉树实现类
05-09
Java的二叉树实现类，是一种常见的数据结构和算法基础。在程序设计中，二叉树广泛应用于搜索、排序、储存、压缩、编码等方面，具有较高的实用价值和研究价值。 Java的二叉树实现可以采用多种方式，例如：链式存储、数组存储、堆存储等。其中，链式存储是一种常见的实现方式，其基本思想是使用节点类来表示树的结构，在每个节点类中保存左子树和右子树的引用信息。 具体实现时，需要定义一个Node类表示一个节点，该类中包含三个属性：data存储节点数据、left存储左子节点的引用、right存储右子节点的引用。通过使用Node类，便可以实现二叉树的遍历、插入、删除、查找等基本操作。 在实现Java的二叉树时，需要注意以下几点：首先，需要定义二叉树的根节点，并在每次操作后实时更新根节点的引用；其次，需要考虑二叉树的节点数据类型，如果节点数据类型不同，则需要使用泛型来处理；最后，需要结合具体应用场景，来灵活运用不同的遍历算法和数据结构，实现高效和优化的代码逻辑。 总之，Java的二叉树实现类虽然简单，但实际应用中却有着广泛的应用。通过深入理解二叉树的基本概念和常见实现方法，可以提高程序设计水平和算法思维能力，为实现更加复杂和高级的数据结构和算法奠定坚实的基础。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值