【机器学习基础】最大边缘分类器

本系列为《模式识别与机器学习》的读书笔记。

一，最大边缘分类器

考察线性模型的⼆分类问题，线性模型的形式为

$$y(\mathbf{x})={\mathbf{w}}^T\mathbf{\varphi }(\mathbf{x})+b\text{\hspace{1em}(7.1)}$$

其中 $\mathbf{\varphi }(\mathbf{x})$ 表⽰⼀个固定的特征空间变换，并且显式地写出了偏置参数 $b$ 。训练数据集由 $N$ 个输⼊向量 ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_N$ 组成，对应的⽬标值为 $t_1,\dots ,t_N$ ，其中 t n ∈ { − 1 , 1 } t_n\in\{−1, 1\} tn​∈{ −1,1} ， 新的数据点 $\mathbf{x}$ 根据 $y(\mathbf{x})$ 的符号进⾏分类。

现阶段，假设训练数据集在特征空间中是线性可分的，即根据定义，存在⾄少⼀个参数 $\mathbf{w}$ 和 $b$ 的选择⽅式，使得对于 $t_n=+1$ 的点，函数(7.1)都满⾜ $y({\mathbf{x}}_n)>0$ ，对于 $t_n=-1$ 的点，都有 $y({\mathbf{x}}_n)<0$ ，从⽽对于所有训练数据点，都有 $t_{n}y({\mathbf{x}}_n)>0$ 。

如果有多个能够精确分类训练数据点的解，那么应该尝试寻找泛化错误最⼩的那个解。 ⽀持向量机解决这个问题的⽅法是：引⼊边缘（margin） 的概念，这个概念被定义为决策边界与任意样本之间的最⼩距离，如图7.1所⽰。

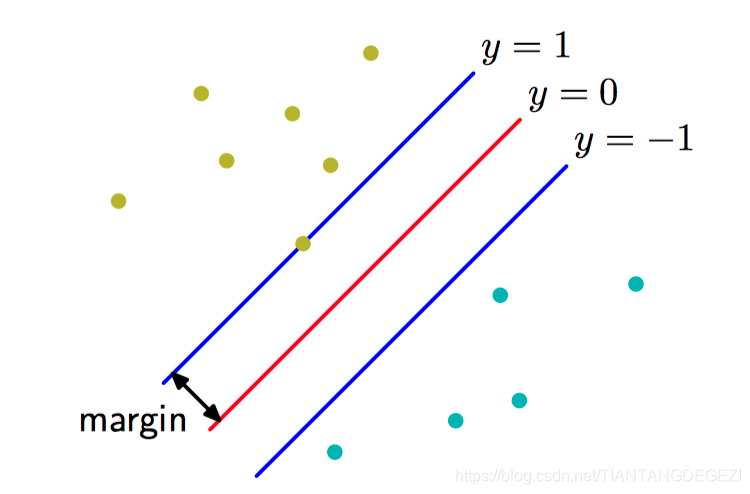
如图7.2，最⼤化边缘会⽣成对决策边界的⼀个特定的选择，这个决策边界的位置由数据点的⼀个⼦集确定，被称为⽀持向量，⽤圆圈表⽰。

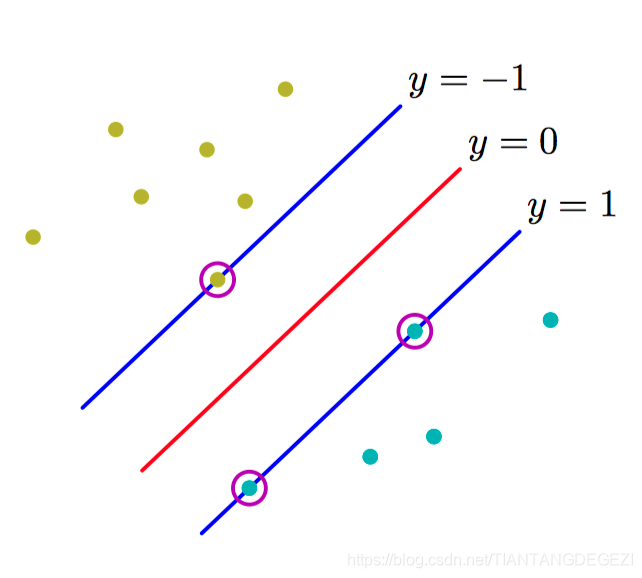
在⽀持向量机中，决策边界被选为使边缘最⼤化的那个决策边界。

点 $\mathbf{x}$ 距离由 $y(\mathbf{x})=0$ 定义的超平⾯的垂直距离为 $\frac{|y(\mathbf{x})|}{\Vert \mathbf{w}\Vert }$ ，其中 $y(\mathbf{x})$ 的函数形式由公式(7.1)给出，我们感兴趣的是那些能够正确分类所有数据点的解，即对于所有的 $n$ 都有 $t_{n}y({\mathbf{x}}_n)>0$ ，因此点 ${\mathbf{x}}_n$ 距离决策⾯的距离为
$$\frac{t_{n}y({\mathbf{x}}_n)}{\Vert \mathbf{w}\Vert }=\frac{t_n({\mathbf{w}}^T\mathbf{\varphi }({\mathbf{x}}_n)+b)}{\Vert \mathbf{w}\Vert }\text{\hspace{1em}(7.2)}$$

边缘由数据集⾥垂直距离最近的点 ${\mathbf{x}}_n$ 给出，希望最优化参数 $\mathbf{w}$ 和 $b$ ，使得这个距离能够最⼤化。因此最⼤边缘解可以通过下式得到：

$$\underset{\mathbf{w},b}{\mathrm{argmax}}\left\{\frac{1}{\Vert \mathbf{w}\Vert }\underset{n}{\min }\left[t_n\left({\mathbf{w}}^T\mathbf{\varphi }\left({\mathbf{x}}_n\right)+b\right)\right]\right\}\text{\hspace{1em}(7.3)}$$

注意到如果进⾏重新标度 $\mathbf{w}\to \kappa \mathbf{w}$ 以及 $b\to \kappa b$ ， 那么任意点 ${\mathbf{x}}_n$ 距离决策⾯的距离 $\frac{t_{n}y({\mathbf{x}}_n)}{\Vert \mathbf{w}\Vert }$ 不会发⽣改变。利用这个性质，对于距离决策⾯最近的点，令

$$t_n({\mathbf{w}}^T\mathbf{\varphi }({\mathbf{x}}_n)+b)=1$$

在这种情况下，所有的数据点会满⾜限制

$$t_n({\mathbf{w}}^T\mathbf{\varphi }({\mathbf{x}}_n)+b)\ge 1,n=1\dots ,N$$

这被称为决策超平⾯的标准表⽰。 对于使上式取得等号的数据点，我们说限制被激活（active），对于其他的数据点，我们说限制未激活（inactive）。根据定义，总会存在⾄少⼀个激活限制，因为总会有⼀个距离最近的点，并且⼀旦边缘被最⼤化，会有⾄少两个激活的限制。这样，最优化问题就简化为了最⼤化 $\Vert \mathbf{w}{\Vert }^{-1}$ ，这等价于最⼩化 $\Vert \mathbf{w}{\Vert }^2$ ，因此我们要在上述限制条件下，求解最优化问题

$$\underset{\mathbf{w},b}{\mathrm{argmin}}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2$$

为了解决这个限制的最优化问题，引⼊拉格朗⽇乘数 $a_n\ge 0$ 。每个限制条件都对应着⼀个乘数 $a_n$ ，从⽽可得下⾯的拉格朗⽇函数

L ( w , b , a ) = 1 2 ∥ w ∥ 2 − ∑ n = 1 N a n { t n ( w T ϕ ( x n ) + b ) − 1 } (7.4) L(\boldsymbol{w},b,\boldsymbol{a})=\frac{1}{2}\|\boldsymbol{w}\|^{2}-\sum_{n=1}^{N}a_n\{t_n(\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_n)+b)-1\}\tag{7.4} L(w,b,a)=21​∥w∥2−n=1∑N​an​{ tn​(wTϕ(xn​)+b)−1}(7.4)

其中 $\mathbf{a}=(a_1,\dots ,a_N{)}^T$ 。令 $L(\mathbf{w},b,\mathbf{a})$ 关于 $\mathbf{w}$ 和 $b$ 的导数等于零，有
$$\begin{gathered} \mathbf{w}=\sum _{n=1}^N{a}_n{t}_n\mathbf{\varphi })({\mathbf{x}}_n) \\ \sum _{n=1}^N{a}_n{t}_n=0 \end{gathered}$$

使⽤这两个条件从 $L(\mathbf{w},b,\mathbf{a})$ 中消去 $\mathbf{a}$ 和 $b$ ，就得到了最⼤化边缘问题的对偶表⽰（dual representation），其中要关于 $\mathbf{a}$ 最⼤化

$$\tilde{L}(\mathbf{a})=\sum _{n=1}^N{a}_n-\frac{1}{2}\sum _{n=1}^N\sum _{m=1}^N{a}_n{a}_m{t}_n{t}_{m}k({\mathbf{x}}_n,{\mathbf{x}}_m)\text{\hspace{1em}(7.5)}$$

其中 $k(\mathbf{x},{\mathbf{x}}^{\prime })=\mathbf{\varphi }(\mathbf{x}{)}^T\mathbf{\varphi }({\mathbf{x}}^{\prime })$，限制条件为

$$\begin{gathered} a_n\ge 0,n=1\dots ,N \\ \sum _{n=1}^N{a}_n{t}_n=0 \end{gathered}$$

通过使⽤公式消去 $\mathbf{w}$ ，$y(\mathbf{x})$ 可以根据参数 { a n } \{a_n\} { an​} 和核函数表⽰，即

$$y(\mathbf{x})=\sum _{n=1}^N{a}_n{t}_{n}k(\mathbf{x},{\mathbf{x}}_n)+b\text{\hspace{1em}(7.6)}$$

满足如下性质：

a n ≥ 0 t n y ( x n ) − 1 ≥ 0 a n { t n y ( x n ) − 1 } = 0 a_n\ge0\\ t_ny(\boldsymbol{x}_n)-1\ge0\\ a_n\{t_ny(\boldsymbol{x}_n)-1\}=0 an​≥0tn​y(xn​)−1≥0an​{ tn​y(xn​)−1}=0

因此对于每个数据点，要么 $a_n=0$ ，要么 $t_{n}y({\mathbf{x}}_n)=1$ 。任何使得 $a_n=0$ 的数据点都不会出现在公式(7.5)的求和式中，因此对新数据点的预测没有作⽤。剩下的数据点被称为⽀持向量（support vector）。

解决了⼆次规划问题，找到了 $\mathbf{a}$ 的值之后，注意到⽀持向量 ${\mathbf{x}}_n$ 满⾜ $t_{n}y({\mathbf{x}}_n)=1$，就可以确定阈值参数 $b$ 的值，可得
t n ( ∑ m ∈ S a m t m k ( x n , x m ) + b ) = 1 (7.7) t_n\left(\sum_{m\in{\mathcal{S}}}a_mt_mk(\boldsymbol{x}_n,\boldsymbol{x}_m)+b\right)=1\tag{7.7} tn​(m∈S∑​a