靠右行驶规则的元胞自动机交通流建模(cellular automata,CA),2014美国数学建模竞赛(MCM)A题

最新推荐文章于 2023-07-05 00:58:52 发布

tinymilk

最新推荐文章于 2023-07-05 00:58:52 发布

阅读量1.2w

点赞数 33

分类专栏：仿真建模文章标签：元胞自动机 NaSch STNS 美国数学建模演化规则

本文链接：https://blog.csdn.net/tinymilk/article/details/19141093

版权

本文介绍了元胞自动机（CA）在数学建模中的应用，特别是用于模拟交通流。从Wolfram的184号规则开始，逐步发展到NaSch规则和双车道模型STNS。接着，文章提出了靠右行驶模型的Keep-Right Rule，该规则通过调整CA的演化规则，实现了符合实际交通规则的仿真。最后，展示了用Matlab实现的靠右行驶规则仿真模拟图，并提供了代码分享的承诺。

摘要由CSDN通过智能技术生成

在这里我并不想说多少和美国数学建模(MCM)相关的东西，但是以2014美赛美赛A题的背景谈谈元胞自动机(Cellular automata,后面简称CA)以及其在数学建模中交通流模型中的作用和实现方法。CA的基本知识，在这里不用多说，其他地方可以搜到很多相关的简介。但是，CA之所以让人着迷，在于她的规则，元胞之间相互作用的演化规则，这些规则就是构成CA的基石，让CA可以做很多意想不到的事情，比如模拟物理现象(沙堆，气体分子运动，光的传播等等)，做图像处理(边缘检测等)，计算机网络建模......

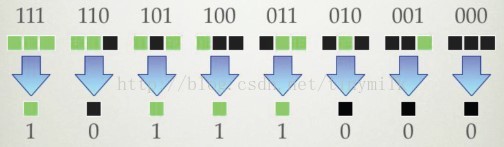
在这里，我们就讨论一下元胞在交通流模型中的应用。众所周知，最简单的元胞交通流模型是wolfram提出的初等CA的第184号规则，其演化规则如下:

figure 1:wolfram的184号规则

这个规则可以让元胞模拟出交通流的感觉，为什么说是感觉呢，因为大家好像看到了一个方块或者说叫一个小车，在向前行进，但是并没有模拟出交通流中的很多现象。随后就有NaSch规则被提出来了，这个规则可以说是所有元胞交通流模型的鼻祖，后面很多规则都是从这个规则中进化而来的。而我们今天讨论的靠右行驶的双车道模型也是根据NaSch模型改进而来的，简单讨论一下NaSch模型，然后进一步引出本文要讲解的靠右行驶模型。

NaSch规则:

(1)加速， $v_{n}\rightarrow min(v_{n}+1,v_{max})$