popcount 算法分析

最新推荐文章于 2023-01-13 20:58:39 发布

致守

最新推荐文章于 2023-01-13 20:58:39 发布

阅读量1.2k

点赞数 1

分类专栏： Algorithm c++

原文链接：https://zhuanlan.zhihu.com/p/341488123

版权

c++ 同时被 2 个专栏收录

291 篇文章 13 订阅

订阅专栏

Algorithm

83 篇文章 19 订阅

订阅专栏

popcount[1]（population count），也叫 sideways sum，是计算一个整数的二进制表示有多少位是1。在一些场合下很有用，比如计算0-1稀疏矩阵（sparse matrix）或位数组（bit array）中非零元素个数、比如计算两个字符串的汉明距离(Hamming distance)。

　　Intel 在2008年的 Nehalem 架构的处理器 Core i7 引入了 SSE4.2 指令集，其中有 CRC32 和 POPCNT 指令，POPCNT可以处理16, 32, 64位整数。后在 AVX-512 指令集引入了向量化的popcount, 叫 VPOPCNTDQ。

　　C++委员会在2020年的 C++20 标准加入了头文件，有判断游戏里的纹理尺寸是否是的函数，不过不叫 isPowerOfTwo，而是 std::has_single_bit ，也有本文即将登场的主角 std::popcount。链接中给出了两种实现方式，前者运算量少。Python则在2021年的 3.10 版本加入了函数 int.bit_count()[2]。

template <std::unsigned_integral T>
//    requires unsigned integral type
constexpr bool has_single_bit(T x) noexcept
{
#if 1
    return x != 0 && (x & (x - 1)) == 0;
#else
    return std::popcount(x) == 1;
#endif
}

　　如今，底层硬件指令和上层库都给予了对 popcount 的支持，生活变得越来越美好。个中的算法，在此也讲解一番，可以提升数学和算法功底。算法大致有以下几种[3]：

iterated_popcnt
sparse_popcnt
dense_popcnt
lookup_popcnt
parallel_popcnt
nifty_popcnt
hacker_popcnt
hakmem_popcnt
assembly_popcnt

　　下面依次给出相关代码和算法分析。

int iterated_popcnt(uint32_t n)
{
    int count = 0;
    for(; n; n >>= 1)
        count += n & 1U;
    return count;
}

　　iterated_popcnt 通过循环查找1位并累加，多少位就循环多少次，简单明了，也是最慢的。

int sparse_popcnt(uint32_t n)
{
    int count = 0;
    while(n)
    {
        ++count;
        n &= n - 1;
    }
    return count;
}

　　sparse_popcnt 对 iterated_popcnt 做了改进，每次迭代总是将最右边的非零位置零。这是减法的妙用。试想一下，一个仅最高位为1的整数，用此方法的话仅需一次迭代；而 iterated_popcnt 还是会“乖乖地”迭代 32 次。

int dense_popcnt(uint32_t n)
{
    int count = 32;  // sizeof(uint32_t) * CHAR_BIT;
    n ^= 0xFF'FF'FF'FF;
    while(n)
    {
        --count;
        n &= n - 1;
    }
    return count;
}

　　dense_popcnt 只是 sparse_popcnt 的一个变种。如果我们有先验条件，知道该数的比特位有很多很多的1（这也是取名 dense 的由来），可以先取反求 popcount，最后用整数类型的位数一减就得到结果。如果数的分布是随机的，即数的0、1位数差不多（not too sparse, not too dense），将失去优势，与 sparse_popcnt 表现一样，如果忽略掉开始的一次取反操作。

　　n & (n-1) 式子还有一个用途，isPowerOfTwo 函数会用上此技巧，就是判断一个整数 x 是否是 2 的 n 次幂。文章末尾会再讲。

int lookup_popcnt(uint32_t n)
{
#if 0  // generate the table algorithmically, and you should put it outside.
    static uint8_t table[256] = {0};
    for(uint32_t i = 1; i < 256; ++i)
        table[i] = table[i>>1] + i & 1U;
    
    const uint8_t* p = reinterpret_cast<const uint8_t*>(&n);
    return table[p[0]] + table[p[1]] + table[p[2]] + table[p[3]];
#else
# define BIT2(n)       n,       n+1,       n+1,       n+2
# define BIT4(n) BIT2(n), BIT2(n+1), BIT2(n+1), BIT2(n+2)
# define BIT6(n) BIT4(n), BIT4(n+1), BIT4(n+1), BIT4(n+2)
# define BIT8(n) BIT6(n), BIT6(n+1), BIT6(n+1), BIT6(n+2)

    static const uint8_t table[256] = {BIT8(0)};
    return table[n & 0xFF] + table[(n>>8) & 0xFF] +
           table[(n>>16) & 0xFF] + table[(n>>24) & 0xFF];
#endif          
}

　　lookup_popcnt 通过查表法，用空间换时间，所以来得快。

这里没有制作整个 uint32_t 或 uint16_t 范围内的表，需要太大空间，不切实际。uint8_t 表可以上高速缓存（cache），来得快。最终分四次求值然后相加。上述代码列出了两种方式来构造表：

1. 利用 f(n) = f(n/2) + n%2, f(0) = 0。直观而且方便移植。不要求 char 一定为8位，即static_assert(CHAR_BIT == 8);，CHAR_BIT 和 UCHAR_MAX 作为宏定义在文件中，平台移植时可能会用到。

2. 利用宏扩展递归展开，很漂亮的写法。上面假定了char为8位，有些旧的机器一个字节7位，就需要作一些修改。

int parallel_popcnt(uint32_t n)
{
#define POW2(c)      (1U << (c))
#define MASK(c)      (static_cast<uint32_t>(-1) / (POW2(POW2(c)) + 1U))
#define COUNT(x, c)  ((x) & MASK(c)) + (((x)>>(POW2(c))) & MASK(c))
	n = COUNT(n, 0);
	n = COUNT(n, 1);
	n = COUNT(n, 2);
	n = COUNT(n, 3);
	n = COUNT(n, 4);
//	n = COUNT(n, 5);  // uncomment this line for 64-bit integers
	return n;
#undef COUNT
#undef MASK
#undef POW2
}

parallel_popcnt 利用了并行计算。下面给出图片解说：

　　想象一下我们已经算好了的每k位一组的 popcount（k = 1是初始值），现在向 2k 位挺进。 , a为高k位，b为低k位，于是结果就为 popcount(n) = a + b。代码里用mask分别屏蔽高低k位取出a和b再加。如此，32位整数需5次迭代，64位整数需6次迭代。

　　关于第k次迭代MASK的值，下面除了左边第一列是二进制外，右边的都是十六进制数。

[0]. 01010101 01010101 01010101 01010101 = 55555555 = FFFFFFFF / (0x2+1)
[1]. 00110011 00110011 00110011 00110011 = 33333333 = FFFFFFFF / (0x4+1)
[2]. 00001111 00001111 00001111 00001111 = 0F0F0F0F = FFFFFFFF / (0x10+1)
[3]. 00000000 11111111 00000000 11111111 = 00FF00FF = FFFFFFFF / (0x100+1)
[4]. 00000000 00000000 11111111 11111111 = 0000FFFF = FFFFFFFF / (0x10000+1)

　　第k次的数的规律是个0，接着个1，如此循环下去。对应高2k位，1对应低2k位。右边的除数是，居然跟费马数(Fermat number)吻合。

　　1640年，费马声称形如的数是质数，欧拉算出是合数，于是被推翻了。这让我联想到了刘慈欣《三体》中提到的农场主假说：一个农场主养了一群火鸡，会在每天中午十一点来给它们喂食。火鸡中的一名科学家（费马）观察到了这个现象（数是质数），一直观察到近一年（k 从 0 到 4）都没有例外，于是它也发现了自己宇宙中的伟大定律：“每天上午十一点，就有食物降临。（猜想数都是质数）”它在感恩节早晨向火鸡们公布这个定律，但这天上午十一点食物没有降临，农场主进来把它们都捉去杀了。费马数猜想虽然是错的，但是高斯发现一个正n边形，当且仅当n为费马素数或为几个不同费马素数的乘积时，才能够用尺规作出图来。于是在19岁便成功证明了正十七边形可以用尺规作图。

int nifty_popcnt(uint32_t n)
{
	constexpr uint32_t max = std::numeric_limits<uint32_t>::max();
	constexpr uint32_t MASK_01010101 = max / 3;
	constexpr uint32_t MASK_00110011 = max / 5;
	constexpr uint32_t MASK_00001111 = max /17;
	n = (n & MASK_01010101) + ((n>>1) & MASK_01010101);
	n = (n & MASK_00110011) + ((n>>2) & MASK_00110011);
	n = (n & MASK_00001111) + ((n>>4) & MASK_00001111);
	return n % 255 ;
}

　　nifty_popcnt 与 parallel_popcnt 开始都一样，只是写法不同，用3次迭代完成了每8位一组的和，不同之处在于末尾用模255一下子结束了运算，较之漂亮(取名 nifty 的由来)！这里面涉及到一些数学知识。

　　一个K进制数B ( )，n表示共有n位数，且，数 B 可以记作。有等式，可以用 二项式展开，或用数学归纳法证明此结论。代入上式，有。于是有结论：一个K进制数模(K-1)的结果，等于此K进制数的各位相加再模K-1。这就是小学里被告知如何判断一个十进制数能否被9整除的方法——每个位上的数加起来能否被9整除。如果位数多，加起来后的数依然很大，你可以再次套用这一法则。

　　于是，如果能确定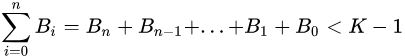的话，就可以加强结论：popcount(B) = B % (K-1)。％是取模操作。上面每8位一组，相当于进制，所以用了255这个数；为了使用上面的等式计算，必须至少得3次迭代。2次迭代创造进制，而对于一个32位整形，popcount 的最大值为32，，所以需要3次迭代。想想一下64位整形 uint64_t，popcount 可能的最大取值是64，这里要选取的数是511。

 int hacker_popcnt(uint32_t n)
{
	n -= (n>>1) & 0x55555555;
	n  = (n & 0x33333333) + ((n>>2) & 0x33333333);
	n  = ((n>>4) + n) & 0x0F0F0F0F;
	n += n>>8;
	n += n>>16;
	return n & 0x0000003F;
}

取名 hacker_popcnt 是因为来自于 Hacker's Delight[4] 这本书。网上有电子版下载，强烈推荐翻阅。书中第5章专门讲 Counting Bits。上面这段代码来自第一节的 Figure 5-2 Counting 1-bits in a word。该段代码在各大开源项目都有。JDK 的 java.lang.Integer 和 java.lang.Long 类中的方法 bitCount，分别对应32位和64位的 popcount，至于任意精度的整数（java.lang.BigInteger ），则通过 Integer#bitCount 方法来计算。FFmpeg 的文件 libavutil/common.h 中也有这段代码。

/*
HAKMEM Popcount

Consider a 3 bit number as being
    4a+2b+c
if we shift it right 1 bit, we have
    2a+b
subtracting this from the original gives
    2a+b+c
if we shift the original 2 bits right we get
    a
and so with another subtraction we have
    a+b+c
which is the number of bits in the original number.

Suitable masking  allows the sums of  the octal digits  in a 32 bit  number to
appear in  each octal digit.  This  isn't much help  unless we can get  all of
them summed together.   This can be done by modulo  arithmetic (sum the digits
in a number by  molulo the base of the number minus  one) the old "casting out
nines" trick  they taught  in school before  calculators were  invented.  Now,
using mod 7 wont help us, because our number will very likely have more than 7
bits set.   So add  the octal digits  together to  get base64 digits,  and use
modulo 63.   (Those of you  with 64  bit machines need  to add 3  octal digits
together to get base512 digits, and use mod 511.)

This is HACKMEM 169, as used in X11 sources.
Source: MIT AI Lab memo, late 1970's.
*/
int hakmem_popcount(uint32_t n)
{
    unsigned int tmp;
    tmp = n - ((n>>1) & 033333333333) - ((n>>2) & 011111111111);
    return ((tmp + (tmp >> 3)) & 030707070707) % 63;
}

　　取名 hakmem_popcnt 是因为来自于 HAKMEM (Hacks Memo)，来自 MIT AI Lab，里面有很多关于数学的有用而且漂亮的算法[5]。这里用到了一个技巧：popcount(n) = n - (n>>1) - (n>>2) - ... - (n>>31) = a31 + a30 + ... + a0。

证明不难，提示：对任意整数k成立。

上面先每三个一组（triplet）计算一下popcount(abc) = popcount(4a+2b+c) = (4a+2b+c) - (2a+b) - a = a+b+c，接着再每两个一组计算一下，最后模63。从上面的 nifty_popcnt 分析得知，其实 popcount(uint32_t) <= 32，用63这个数模就够了，因为63是满足的最小数。于是n=6，表示我们需要获得每6位一求的结果。6=3x2，这就是上面先三个再两个的原因。而 nifty_popcnt 两次都是每两个一组。

int assembly_popcnt(uint32_t n)
{
#ifdef _MSC_VER  // Intel style assembly
    __asm popcnt eax,n;
#elif __GNUC__  // AT&T style assembly
    __asm__("popcnt %0,%%eax"::"r"(n));
#else
#error "other POPCNT implementations go here"
#endif
}

　　最终来到了汇编指令 POPCNT，对不熟悉汇编语言的同学，这里稍微讲一下。汇编语言有两种style：Intel 和 AT&T。语法都一样，只是记法不同。之间的区别自行 Google 学习。
Visual C++ 用的是 Intel style，类UNIX 使用 AT&T style。大学的微机原理课程学的是前面一种。个人觉得 Intel 的简单易懂，上面的一行指令可已证明。然后 C/C++函数的返回值都是存入 EAX 寄存器的，所以你看不到 return 语句。函数很简短，所以被调用的时候可以直接 inline 到其他函数。

　　关于汇编指令的用法，请查阅 Intel 官方手册，传送门。现在的机器大都支持了（不支持的虽编译通过，但运行出错），但最好先检测一下。 Linux 平台通过 cat /proc/cpuinfo | grep popcnt 命令就可以看到是否支持。

Before an application attempts to use the POPCNT instruction, it must check that the processor supports SSE4.2 (if CPUID.01H:ECX.SSE4_2[bit 20] = 1) and POPCNT (if CPUID.01H:ECX.POPCNT[bit 23] = 1).

　　asm 可以用来在 C/C++ 代码中插入汇编指令，然后 asm 本来是 C++ 的关键字的，编译器都不能好好地支持。Visual C++编译器不支持ARM、x64平台插入汇编[6]。MSDN上说

The __asm keyword replaces C++ asm syntax. asm is reserved for compatibility with other C++ implementations, but not implemented. Use__asm.

如果用 GCC 编译器的话，可以使用asm，但编译的时候要用 gcc popcnt.c -o bitcnt -std=c99 -fasm，-fasm是让编译器认"asm", "inline" or "typeof"为关键字。
GNU编译器也内置了很多函数，也包括 int __builtin_popcount (unsigned int x);，自 GCC 3.4 版本（2004年）。如果你的机器架构支持的话，会直接译成一条CPU指令。

测试

　　到这里，9种方法都讲完了。接下来需要测试功能和评估效率了。完整代码见这里。

0. method iterated_popcnt uses 2.049E-08s
1. method   sparse_popcnt uses 1.2648E-08s
2. method    dense_popcnt uses 1.6073E-08s
3. method   lookup_popcnt uses 2.49373E-09s
4. method parallel_popcnt uses 3.71119E-09s
5. method    nifty_popcnt uses 3.97232E-09s
6. method   hacker_popcnt uses 3.42209E-09s
7. method   hakmem_popcnt uses 4.68241E-09s
8. method assembly_popcnt uses 2.10791E-09s

　　仅测试32位整形(uint32_t)，你可以修改测试一下64位整形(uint64_t)。Microsoft Visual C++的64位编译器不支持内嵌汇编，可以通过编译器提供的 intrinsic function 或者用32位分两次求和。注意先验证每种方法的正确与否后做benchmark。

　　函数运行时间极短，可能就三四个CPU cycle，可以累加多次运行时间，然后取平均值。方法如同测量纸张的厚度，一张纸难用游标卡尺测量，但是一本厚数就很容易测量，测量了一本书的厚度，又知道了书的页数，用除法就得到了纸张的厚度。

　　用 std::clock() 计时的话，注意使用 CLOCKS_PER_SEC 宏，因为各平台定义的数值不一样。

Linux 平台 /usr/include/bits/time.h

#define CLOCKS_PER_SEC 1000000l

Windows 平台 Microsoft Visual Studio 10.0/VC/include/time.h

#define CLOCKS_PER_SEC  1000

结论

对比 popcount 的各种算法，高效在于能利用并行计算，去掉循环，使用减法和模运算。
通过减1的循环算法(sparse/dense)在知道数只有三五位为1（或0）的话，其实效率也不赖。
查表法的效率挺不错的，如果没有硬件指令的支持，选用这个是可以的。
Hacker's Delight 中的算法，在开源项目中广为引用。
算法就是要充分挖掘求解问题里的数学知识。

参考

^Hamming weight https://en.wikipedia.org/wiki/Hamming_weight
^What’s New In Python 3.10 https://docs.python.org/3.10/whatsnew/3.10.html
^Fast Bit Counting https://gurmeet.net/puzzles/fast-bit-counting-routines/index.html
^Hacker's_Delight_2nd.pdf http://www.hackersdelight.org/
^HAKMEM (bit counting is memo number 169), MIT AI Lab, Artificial Intelligence Memo No. 239, February 29, 1972. http://www.inwap.com/pdp10/hbaker/hakmem/hakmem.html
^Inline assembly is not supported on the ARM and x64 processors. https://github.com/MicrosoftDocs/cpp-docs/blob/master/docs/assembler/inline/inline-assembler.md

https://zhuanlan.zhihu.com/p/341488123

致守

关注

1
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
popcount 算法分析

popcount[1]（population count），也叫 sideways sum，是计算一个整数的二进制表示有多少位是1。在一些场合下很有用，比如计算0-1稀疏矩阵（sparse matrix）或位数组（bit array）中非零元素个数、比如计算两个字符串的汉明距离(Hamming distance)。　　Intel 在2008年的Nehalem架构的处理器 Core i7 引入了SSE4.2指令集，其中有 CRC32 和 POPCNT 指令，POPCNT可以处理16, 32, 64...
复制链接

扫一扫