Solitaire
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2611 Accepted Submission(s): 850
Problem Description
Solitaire is a game played on a chessboard 8x8. The rows and columns of the chessboard are numbered from 1 to 8, from the top to the bottom and from left to right respectively.
There are four identical pieces on the board. In one move it is allowed to:
> move a piece to an empty neighboring field (up, down, left or right),
> jump over one neighboring piece to an empty field (up, down, left or right).
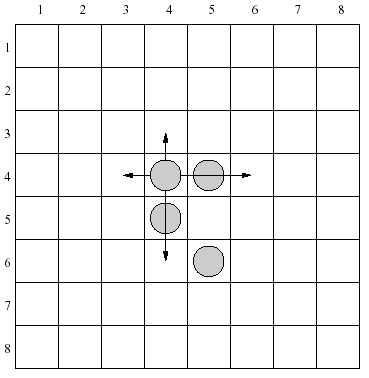
There are 4 moves allowed for each piece in the configuration shown above. As an example let's consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.
Write a program that:
> reads two chessboard configurations from the standard input,
> verifies whether the second one is reachable from the first one in at most 8 moves,
> writes the result to the standard output.
There are four identical pieces on the board. In one move it is allowed to:
> move a piece to an empty neighboring field (up, down, left or right),
> jump over one neighboring piece to an empty field (up, down, left or right).

There are 4 moves allowed for each piece in the configuration shown above. As an example let's consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.
Write a program that:
> reads two chessboard configurations from the standard input,
> verifies whether the second one is reachable from the first one in at most 8 moves,
> writes the result to the standard output.
Input
Each of two input lines contains 8 integers a1, a2, ..., a8 separated by single spaces and describes one configuration of pieces on the chessboard. Integers a2j-1 and a2j (1 <= j <= 4) describe the position of one piece - the row number and the column number respectively. Process to the end of file.
Output
The output should contain one word for each test case - YES if a configuration described in the second input line is reachable from the configuration described in the first input line in at most 8 moves, or one word NO otherwise.
Sample Input
4 4 4 5 5 4 6 5 2 4 3 3 3 6 4 6
Sample Output
YES
Source
感想:
哎。。。!这题又坑了我一下午。后来发现是一个小错误导致WA了--输入的数据应该减1后再处理 

题目还是蛮卡内存的,dbfs第一次被逼到只开一个char数组判重。
题意:
在一个8×8的棋盘中,给定你4个棋子A,再给你4个棋子B,问你在8步之内能不能够从A位置移动到B位置;
规则:棋子能能上下左右移动,同时能跳过相邻的棋子到达相邻棋子的空地方。
规则:棋子能能上下左右移动,同时能跳过相邻的棋子到达相邻棋子的空地方。
思路:
还是蛮明显的,8维数组判重,直接模拟棋子的移动就够了。状态有点多,最好用dbfs,因为只要判断YES、NO,我用了一个伪dbfs--先正着搜4步,然后反着搜,如果已经标记了的话就输出YES,否则就NO。
陷阱:
4个棋子是没有区别的,所以最好将棋子排序,避免状态是一样的,但是在程序中状态却不一样。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
int n,m,ans;
char vis[8][8][8][8][8][8][8][8];
int dx[]= {-1,1,0,0};
int dy[]= {0,0,-1,1};
bool mp[8][8]; // 用来判断每一时刻棋盘上某一位置有无棋子
struct Node
{
int x,y;
} p1[4],p2[4];
struct node
{
int step;
Node pp[4];
} cur,now;
queue<node>q1,q2;
bool cmp(const Node&xx1,const Node&xx2) // 从小到大排序
{
if(xx1.x!=xx2.x) return xx1.x<xx2.x;
return xx1.y<xx2.y;
}
bool bfs()
{
int i,j,nst,tst,nstep,nx,ny,tx,ty;
memset(vis,0,sizeof(vis));
memset(mp,0,sizeof(mp));
while(!q1.empty()) q1.pop();
sort(p1,p1+4,cmp);
for(i=0; i<4; i++)
{
cur.pp[i]=p1[i];
}
cur.step=0;
vis[p1[0].x][p1[0].y][p1[1].x][p1[1].y][p1[2].x][p1[2].y][p1[3].x][p1[3].y]='1';
q1.push(cur);
while(!q1.empty()) // 初始状态向前走4步 走过的标记为‘1’
{
now=q1.front();
q1.pop();
nstep=now.step;
if(nstep>=4) break ;
for(i=0; i<4; i++) // 放棋子
{
mp[now.pp[i].x][now.pp[i].y]=1;
}
for(i=0; i<4; i++) // 第几个piece
{
nx=now.pp[i].x;
ny=now.pp[i].y;
for(j=0; j<4; j++) // u d l r
{
cur=now; // 这行代码需加在这里 而不是上面
cur.step=nstep+1;
tx=nx+dx[j];
ty=ny+dy[j];
if(tx<0||tx>=8||ty<0||ty>=8) continue ;
if(mp[tx][ty]) // 如果前面是棋子 则跳过棋子
{
tx+=dx[j];
ty+=dy[j];
if(tx<0||tx>=8||ty<0||ty>=8||mp[tx][ty]) continue ;
}
cur.pp[i].x=tx;
cur.pp[i].y=ty;
sort(cur.pp,cur.pp+4,cmp);
if(!vis[cur.pp[0].x][cur.pp[0].y][cur.pp[1].x][cur.pp[1].y][cur.pp[2].x][cur.pp[2].y][cur.pp[3].x][cur.pp[3].y])
{
vis[cur.pp[0].x][cur.pp[0].y][cur.pp[1].x][cur.pp[1].y][cur.pp[2].x][cur.pp[2].y][cur.pp[3].x][cur.pp[3].y]='1';
q1.push(cur);
}
}
}
for(i=0; i<4; i++) // 拿走棋子
{
mp[now.pp[i].x][now.pp[i].y]=0;
}
}
memset(mp,0,sizeof(mp));
while(!q2.empty()) q2.pop();
sort(p2,p2+4,cmp);
for(i=0; i<4; i++)
{
cur.pp[i]=p2[i];
}
cur.step=0;
if(vis[p2[0].x][p2[0].y][p2[1].x][p2[1].y][p2[2].x][p2[2].y][p2[3].x][p2[3].y]) return true;
else vis[p2[0].x][p2[0].y][p2[1].x][p2[1].y][p2[2].x][p2[2].y][p2[3].x][p2[3].y]='2';
q2.push(cur);
while(!q2.empty()) // 最终状态向后走4步
{
now=q2.front();
q2.pop();
nstep=now.step;
if(nstep>=4) break ;
for(i=0; i<4; i++)
{
mp[now.pp[i].x][now.pp[i].y]=1;
}
for(i=0; i<4; i++) // 第几个piece
{
nx=now.pp[i].x;
ny=now.pp[i].y;
for(j=0; j<4; j++) // u d l r
{
cur=now;
cur.step=nstep+1;
tx=nx+dx[j];
ty=ny+dy[j];
if(tx<0||tx>=8||ty<0||ty>=8) continue ;
if(mp[tx][ty])
{
tx+=dx[j];
ty+=dy[j];
if(tx<0||tx>=8||ty<0||ty>=8||mp[tx][ty]) continue ;
}
cur.pp[i].x=tx;
cur.pp[i].y=ty;
sort(cur.pp,cur.pp+4,cmp);
if(!vis[cur.pp[0].x][cur.pp[0].y][cur.pp[1].x][cur.pp[1].y][cur.pp[2].x][cur.pp[2].y][cur.pp[3].x][cur.pp[3].y])
{ // 没有标记过就标记为‘2’
vis[cur.pp[0].x][cur.pp[0].y][cur.pp[1].x][cur.pp[1].y][cur.pp[2].x][cur.pp[2].y][cur.pp[3].x][cur.pp[3].y]='2';
q2.push(cur);
} // 已经标记为‘1’ 说明在能走到
else if(vis[cur.pp[0].x][cur.pp[0].y][cur.pp[1].x][cur.pp[1].y][cur.pp[2].x][cur.pp[2].y][cur.pp[3].x][cur.pp[3].y]=='1') return true ;
}
}
for(i=0; i<4; i++)
{
mp[now.pp[i].x][now.pp[i].y]=0;
}
}
return false ;
}
int main()
{
int i,j,xx,yy;
while(~scanf("%d%d",&xx,&yy))
{
p1[0].x=xx-1;
p1[0].y=yy-1;
for(i=1; i<4; i++)
{
scanf("%d%d",&xx,&yy);
p1[i].x=xx-1;
p1[i].y=yy-1;
}
for(i=0; i<4; i++)
{
scanf("%d%d",&xx,&yy);
p2[i].x=xx-1;
p2[i].y=yy-1;
}
if(bfs()) printf("YES\n");
else printf("NO\n");
}
return 0;
}





















 685
685

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








