sko.GA实现遗传算法的源码解析

最新推荐文章于 2025-05-09 22:14:47 发布

tommy___2005

最新推荐文章于 2025-05-09 22:14:47 发布

阅读量1.5w

点赞数 57

CC 4.0 BY-SA版权

文章标签： python 算法机器学习

本文链接：https://blog.csdn.net/tommy___2005/article/details/113371798

本文探讨了遗传算法的收敛性原理，介绍了scikit-opt库中遗传算法的实现细节及应用案例，包括参数配置、适应度评估、选择、交叉与变异操作。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、前言

最近在研究机器学习，在学习遗传算法时，发现了scikit-opt（简称sko）项目，这是一个用python实现的群体智能算法项目，包括了遗传算法GA的实现，相关文档在https://scikit-opt.github.io/scikit-opt/#/zh/README上。我对这个算法进行了研究，现在把研究的心得记录成文。

关于遗传算法的理论研究在网上有大量的文章可以查阅，本文不描述遗传算法的理论思想和步骤，仅谈谈个人对遗传算法为什么会收敛的一点认识。刚开始学习遗传算法，误认为遗传算法在基因选择，交叉，变异过程中发生的随机行为无法保证迭代过程不断趋近最优解，是一种随机算法。但在我研究了sko实现GA后，我对GA的收敛性有了新的认识。基因选择决定了GA的收敛，而基因的交叉和变异恰恰与基因选择相反，阻止算法收敛。为什么要设计一些过程去阻止算法收敛呢，目的要防止算法在未取到最优解前就收敛被视为“算法早熟”的情形出现。因此只要满足在经过基因交叉和变异后，上一代存在的最优染色体不被淘汰的这一条件，就能保证算法收敛。同时只要经过足够多轮的基因交叉和变异，就会找到算法的最优染色体。有了这两点的保证，算法就能找到最优解并收敛。要保证算法收敛，交叉算子和变异算子的波动要小，否则遗传算法就退化为随机算法。基于上述认识，就可以研究出一些关于遗传算法的优化算法。由于sko记录了每一代最优染色体，较好的规避了交叉和变异算子的波动不应设置过大导致算法不收敛的问题，反而宜将变异算子的波动设置较大，以便及早出现算法最优解。

二、sko的GA概述

sko的GA的安装采用pip工具，相应教程可在网上找到。项目安装在python运行目录下的site-packages\sko下，文件结构为：

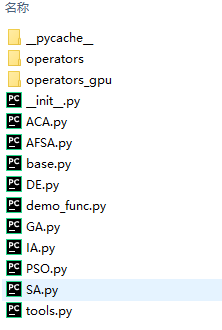
GA.py为实现遗传算法的模块文件，包含3个类，其中GeneticAlgorithmBase和GA实现了利用遗传算法求最小值。

三、如何使用sko的GA

1、关于求值函数的定义

在GeneticAlgorithmBase类（抽象类）的初始化函数中除了完成变量赋值外，有一个非常重要的函数func_transformer(func)，该函数完成对求值函数的转换，如果不能透彻理解这个函数，将不能正确使用sko的GA来求解你的问题。

func_transformer定义在tools.py文件模块中：

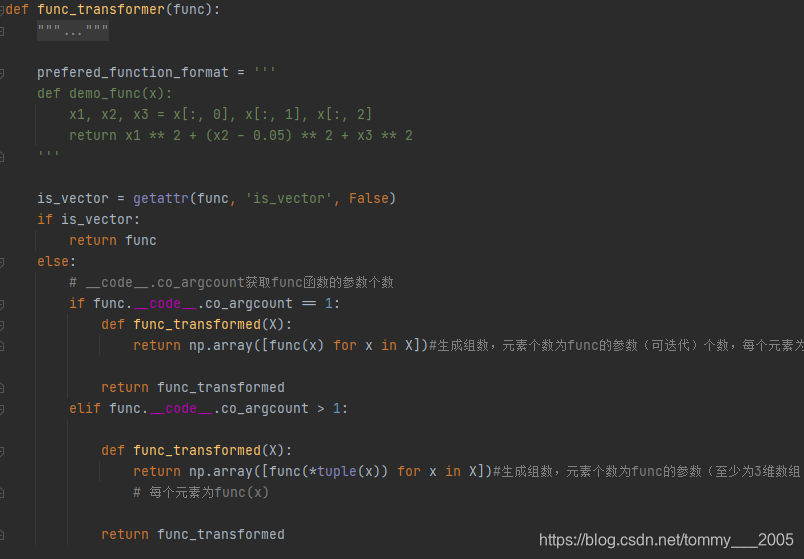
参数func是你定义的求值函数。该参数如果为向量，则返回函数本身，否则将求值函数的格式转换为函数func_transformed，这是一个np数组[demo_func(x),demo_func(x),...,demo_func(x)]

func_transformed在计算求值函数的值时被调用

self.X为当前子代的解空间（十进制表示），是一个二维数组。self.Y_raw是在不存在约束条件时的求值函数值，是一个一维数组，self.Y_raw= [demo_func(x),demo_func(x),...,demo_func(x)]，规定每个元素应为数值。因此，定义的求值函数的返回值应该为数值。举例描述定义的求值函数经过func_transformed转换的结果情况。比如定义的求值函数为

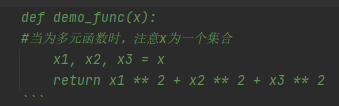
，且对应的self.X=[[20,10,2],[10,40,5],[60,9,7]]，那么self.Y_raw = [demo_func([20,10,2]),demo_func([10,40,5]),demo_func([60,9,7])]=[20**2+10**2+2**2, 10**2+40**2+5**2, 60**2+9**2+7**2]

当然也能将求值函数设置成这样

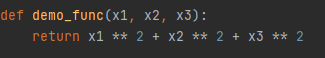
此时求值函数的参数个数超过1，func_transformer(func)将求值函数格式转换为[demo_func(x1，x2, x3)，demo_func(x1，x2, x3)，..demo_func(x1，x2, x3)]= [demo_func([20,10,2]),demo_func([10,40,5]),demo_func([60,9,7])]，达到同样的效果。

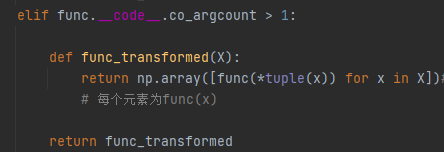
如果求值函数的参数数量为1个，应通过取出数组中的元素，确保求值函数的返回值为数值，如：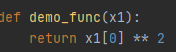

2、关于约束元组的定义

在GeneticAlgorithmBase类初始化方法中，定义了两个为元组类型的可选参数penalty_eq和penalty_ueq，用于定义求值函数自变量的取值范围。

约束函数的执行语句为：

其思想为假设self.X不满足约束条件，那么1e5 * penalty_eq + 1e5 * penalty_ueq的值较大，相应的self.Y值也较大，进而阻止其被选为最优解，使得self.X被淘汰。要保持self.Y = self.Y_raw，必须要确保penalty_eq和 penalty_ueq的值为0。其中penalty_eq为0的条件是元组penalty_eq中的每个元素c_i(x)为0，penalty_ueq为0的条件是元组penalty_ueq中的每个元素c_i(x)小于等于0。constraint_eq定义等式的约束，penalty_ueq定义不等式的约束。比如：

当x[1]+x[2]等于1时，constraint_eq每个元素为0，当1=<x[1]*x[2]<=5时，penalty_ueq每个元素小于等于0。

3、实例

在给出实例之前，简要介绍如何实例化GA和调用函数。

（1）实例化GA

GA是GeneticAlgorithmBase类的具体类，要使用new GA()生成GA的实例化后，才能使用GA算法。GA类的参数如下：

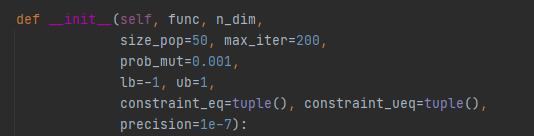
其中func为自定义的求值函数，n_dim为求值函数的自变量维度，size_pop为每一次迭代时的染色体数目，max_iter为迭代的次数，prop_mut为变异因子，lb为求值函数自变量的最小值，ub为求值函数自变量的最大值，constraint_eq为求值函数自变量等式约束，penalty_ueq为求值函数自变量的不等式约束，precision为求值函数自变量的精度。其中参数func、constraint_eq、penalty_ueq是使用GA的重点。

（2）在GA实例化后，要调用run方法，才能执行GA算法。sko还提供了用于并行计算的pytorch提高算法性能的to方法。比如：ga.to("cuda:2")，ga为GA类的实例。

（3）用GA算法拟合曲线的实例

用GA算法实现二元二次函数（Y=6*X1*X1+3*X2*X2+4*X1*X2+5*X1+9*X2+7或Y=7*X1*X1-4*X2*X2+10*X1*X2+10*X1+4*X2+7）的回归。

训练样本为（只取后三列数据）

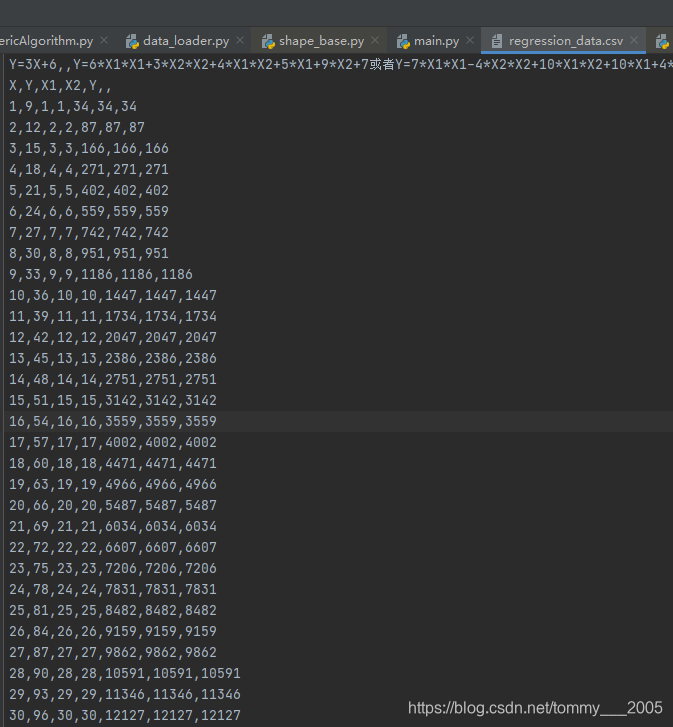
首先定义求值函数。这里采用均方差表示回归函数的最小误差，求值函数使用向量形式表示为： $f(w)=(xw-y)^T(xw-y)$ ,其中 $x=\begin{bmatrix} x11*x11,x12*x12,x11*x12,x11,x12,1 \\ x21*x21,x22*x22,x21*x22,x21,x22,1\\ .... ... .... ................... ........................\\ x[30]1*x[30]1,x[30]2*x[30]2,x[30]1*x[30]2,x[30]1,x[30]2,1 \end{bmatrix}$ ， $w=\begin{bmatrix} w1\\ w2\\ w3\\ w4\\ w5\\ w6 \end{bmatrix}$ ， $y=\begin{bmatrix} y1\\ y2\\ ...\\ y30 \end{bmatrix}$ 。用mean_square_error_func方法定义求值函数。需注意两点，一是输入的参数p为行向量（为GA算法的规定），因此需要先将p转化为列向量用于计算。二是求值函数的值为数值，因此对np.dot(xwy.T, xwy)值为矩阵（里面只有一个元素）取出其第一个元素作为求值函数的返回值。

另外，由于自变量w的维度为6，故将n_dim的值设置为6。设置每一次迭代的染色体数目size_pop为50（这个数量不要太小，否则须设置较大的迭代次数来取得较好的收敛效果），将迭代次数max_iter设置为500，将w中各元素的最小值lb和最大值ub均设置为[-10,10]，也可以单独对各元素设置，比如：lb=[-1,1,2,3,4,1]，ub=[1,5,20,30,42,12]，将w的精度precision设置为1（即为整数），将变异因子prop_mut设置为0.05（建议设置为0到1之间更大的值）。这里没有约束条件，因此不设置constraint_eq和penalty_ueq。代码如下：

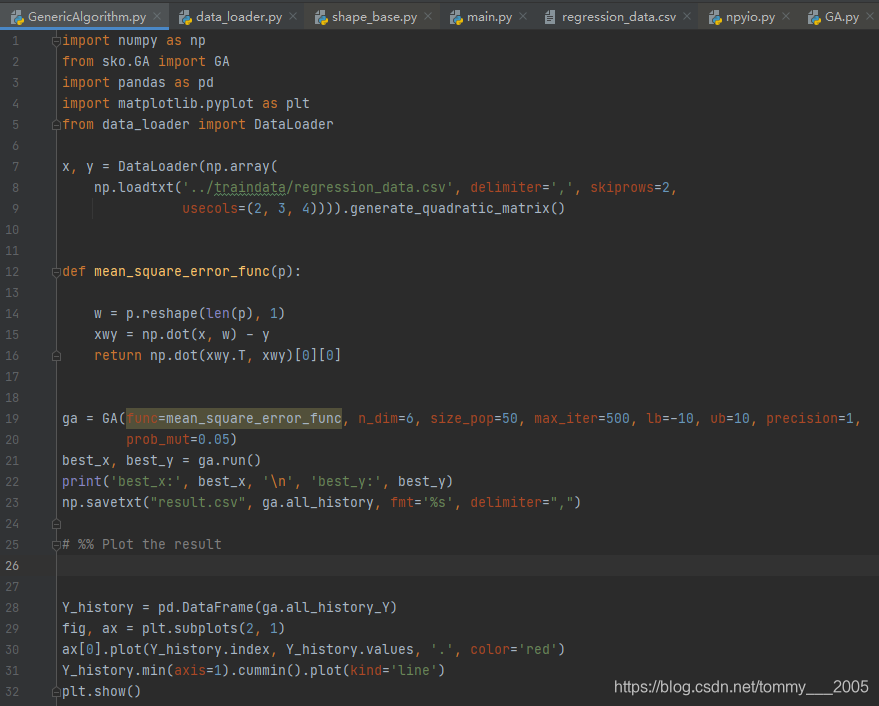
结果如下：

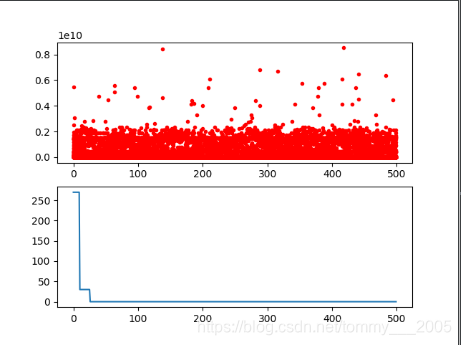
误差为0，完全拟合，效果非常好。

四、GA算法实现的原理

在功能架构上，抽象类GeneticAlgorithmBase实现了GA算法的适应度评估函数以及定义了GA算法流程，并选出算法最优解，还记录了GA算法过程中的重要数据。具体类GA实现了基因的编码、初始化，定义了适应度评估函数、选择、交叉、变异的过程，这些过程分别在ranking、selection、crossover、mutation模块中实现。下文介绍GeneticAlgorithmBase类、GA类、ranking、selection、crossover、mutation模块的相关逻辑。

1、GeneticAlgorithmBase类的实现逻辑

GeneticAlgorithmBase类采用模式设计中的模板方法定义了GA算法的流程。设计GA算法循环max_iter次，在每次循环中，首先将染色体（未实现染色体的产生）映射回解空间，然后计算求值函数，接着对染色体进行适应度评估，然后依次进行选择、交叉、变异，在此过程中，记录了每一代染色体适应度评估函数的最大值及其对应的解空间和求值函数的值。循环结束后，从历史记录中选出最优解空间。

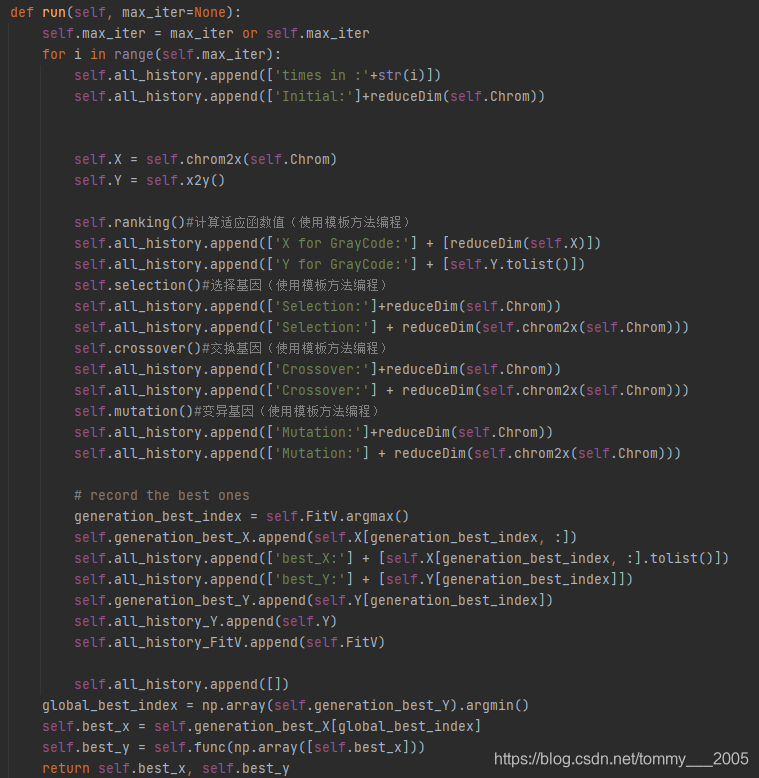
2、GA类的实现逻辑

（1）初始化方法

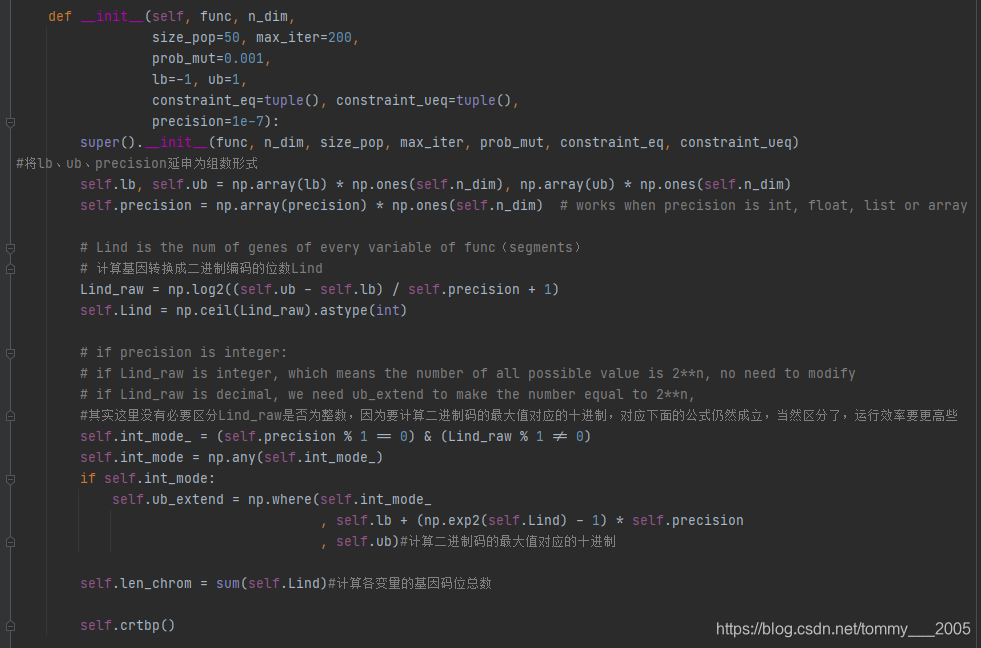
在初始化方法中，完成三项任务，一是计算采用二进制编码解空间所形成的染色体的位数（二进制编码方法在网上有讲解）。编码公式为：Lind= $\left \lceil \log_{2}\frac{lb-ub}{precision}+1 \right \rceil$ 。二是计算染色体空间的最大值对应的十进制，即二进制最高位为1，其余位为0，计算公式为： $ub\_extend=lb+(2^{Lind}-1)*precision$ 。比如，lb=2,ub=12，precision=2，那么解空间为{2，4，6，8，10，12}，染色体的位数为 $\left \lceil \log_{2}(\frac{12-2}{2}+1) \right \rceil=3$ ，染色体空间的最大值对应的十进制数为 $2+(2^{3}-1)*2=16$ 。三是初始化染色体群体。crtbp方法随机生成染色体群体Chrom，这是一个由size_pop行， $\sum_{i=1}^{n}Lind(i)$ （其中Lind(i)为自变量的第i维对应的基因位数）列组成的数值为0或1的二维数组，即生成了size_pop个染色体，每个染色体为一组基因，每组基因由自变量各个维度的基因序列组成。

（2）chrom2x方法

这是一个将染色体映射回解空间的方法。

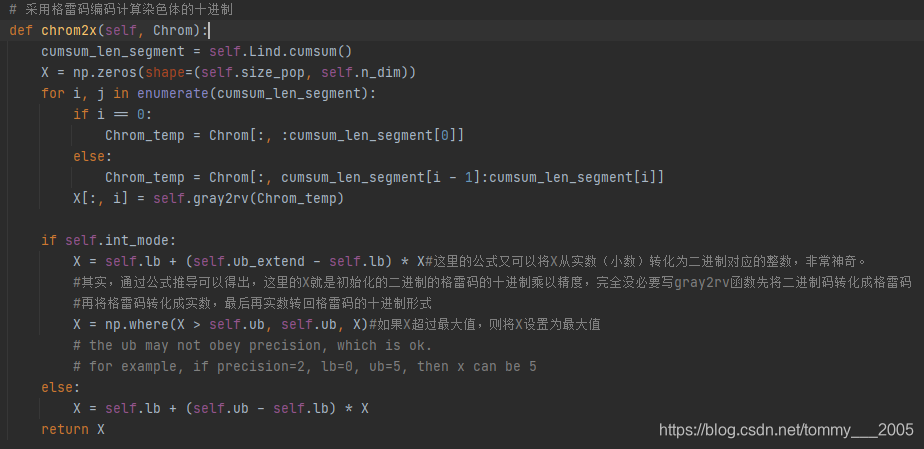
本方法将自变量的各个维度对应的基因序列映射成十进制，形成的X即为解空间Self.X，是一个size_pop行，n_dim列的二维数组。实现过程为：首先使用cumsum方法和for循环，提取Chrom数组各行中的自变量各个维度的基因序列到Chrom_temp中，然后将Chrom_temp映射成实数，最后又将实数转回十进制整数，如果转回的十进制整数超过最大值ub，则设置成ub，以确保解空间在函数定义域内。接下来分析这种方法的本质并提出优化建议。

（3）gray2rv方法

采用格雷码（不是传统的格雷码）将二进制映射成实数。

通过gray_code.cumsum(axis=1) % 2进行格雷码编码，实质是第一位不变，以后各位“遇到1变反，遇到0不变”。如对1001010编码，原码1001010第1位为1，所以其格雷码的第1位也为1，原码第2为0，根据“遇到1变反，遇到0不变”的规则，格雷码的第2位不变，与编码后的第1位相同，因此仍然为1。同理，格雷码的第3位也为1。原码第4位为1，格雷码第4位要在第3位的基础上变反，所以为0。依次类推，格雷码的第5位不变，依然为0，第6位变反，为1，第7位不变，为1，所以格雷码为：1110011。可分析得出，该格雷码的汉明距离为2。以0-15编码为例，3和4的格雷码的汉明距离为2。因此，这种编码不是传统意义的格雷码，传统格雷码的汉明距离为1。

二进制码	格雷码	传统格雷码	十进制
000	000	000	0
001	001	001	1
010	011	011	2
011	010	010	3
100	111	110	4
101	110	111	5
110	100	101	6
111	101	100	7

然后通过mask = np.logspace(start=1, stop=len_gray_code, base=0.5, num=len_gray_code)，(b * mask).sum(axis=1) / mask.sum()将格雷码映射成实数。相应的等式为：，n为格雷码的位数，gray(i)为格雷码第i位（从左往右数）上的值。该等式可变化为：，C为所有数位均为1的格雷码对应的十进制。进一步发现，分子就是格雷码的十进制，分母就是其二进制的最大值。于是,gray为格雷码的十进制。因此gray2rv方法本质上是将格雷码的十进制除以其二进制的最大值，实现二进制到实数的编码转换。另外不难发现。将mask代入chrom2x中将实数转回整数的语句：X = self.lb + (self.ub_extend - self.lb) * X，对X进行化简：

$X=lb+(ub\_extend-lb)*X=lb+(ub\_extend-lb)*mask=$ $lb+(ub\_extend-lb)*\frac{gray}{C}$

$\because ub\_extend=lb+(2^{Lind}-1)*precision$

$\therefore X=lb+(ub\_extend-lb)*\frac{gray}{C}=$ $lb+(lb+(2^{Lind}-1)*precision-lb)*\frac{gray}{2^{Lind}-1}=lb+gray*precision$

因此可以直接利用这一结果优化chrom2x方法。

3、ranking模块的实现逻辑

在ranking类中实现了对染色体的适应度评估，由于求值函数是求函数的最小值，所以将评估函数设置为求值函数的相反数。因此如果将代码改成：self.FitV=self.Y，就可以实现最大值的函数求解。

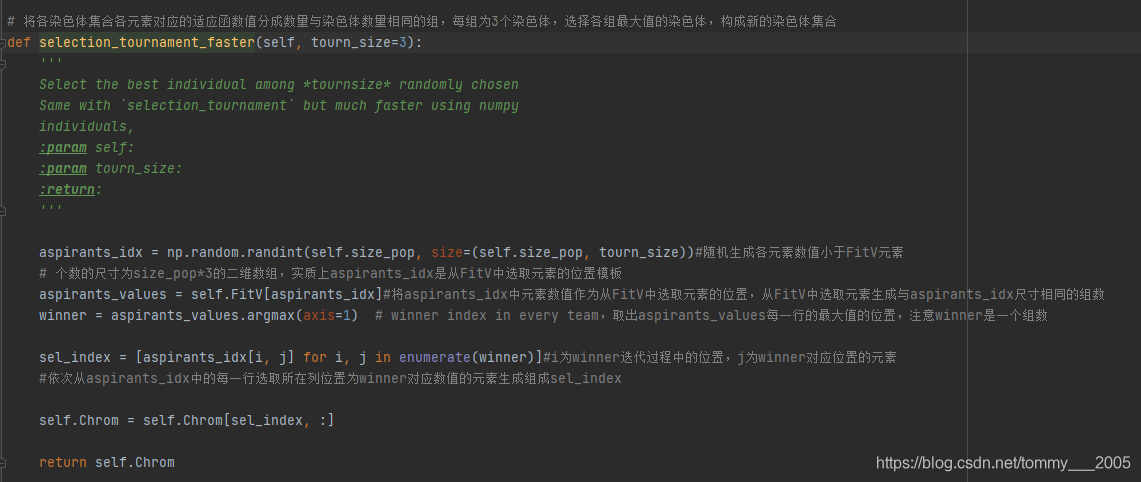
4、selection模块的实现逻辑

该模块通过定义选择模板实现在染色体集合中选择较优的染色体，组成新的染色体集合。为形象说明该过程，举一例子。比如染色体群体 $Chrome=\begin{bmatrix} 0,1,1,0,1,0,1,0 \\ 1,0,1,0,1,0,1,0 \\ 0,1,1,0,1,0,1,0\\ 1,1,1,1,1,0,1,1\\ 0,0,0,0,0,0,1,0 \end{bmatrix}$ ，对应的适应度评估值为 $FitV=\begin{bmatrix} 1.5\\ 2\\ 12\\ 3.6\\ 6,2 \end{bmatrix}$ 。随机生成选择模板，其中每个元素为不大于染色体个数的整数，假设生成的选择模板为 $aspirants_idx=\begin{bmatrix} 1 ,2,3 \\ 3,4,1 \\ 4,4,3\\ 2,3,5\\ 2,2,5 \end{bmatrix}$ 。从FitV中随机选择元素构成新的数组，选取的规则为每次选择3个元素构成新数组的一行，假设形成的新数组 $aspirants_values=\begin{bmatrix} 1.5 ,2 ,12\\ 12,3.6,1.5 \\ 3.6,3.6,12\\ 2,12,6.2\\ 2,2,6.2 \end{bmatrix}$ 。接着取每行中最大值所在的位置，得到 $winner=\begin{bmatrix} 2\\ 0\\ 2\\ 1\\ 2 \end{bmatrix}$ 。然后在选择模板中的每一行选取位置为winner对应值的元素 $sel\_index=\begin{bmatrix} 3\\ 3\\ 3\\ 3\\ 5\end{bmatrix}$ 为需要在Chrome中选取染色体的位置。最后更新染色体 $Chrom=\begin{bmatrix} 0,1,1,0,1,0,1,0 \\ 0,1,1,0,1,0,1,0 \\ 0,1,1,0,1,0,1,0 \\ 0,1,1,0,1,0,1,0 \\ 0,0,0,0,0,0,1,0\\ \end{bmatrix}$ 。可以发现选择的染色体为适应度评估函数值较大的染色体，因此该过程能够淘汰适应度评估函数值较小的染色体。

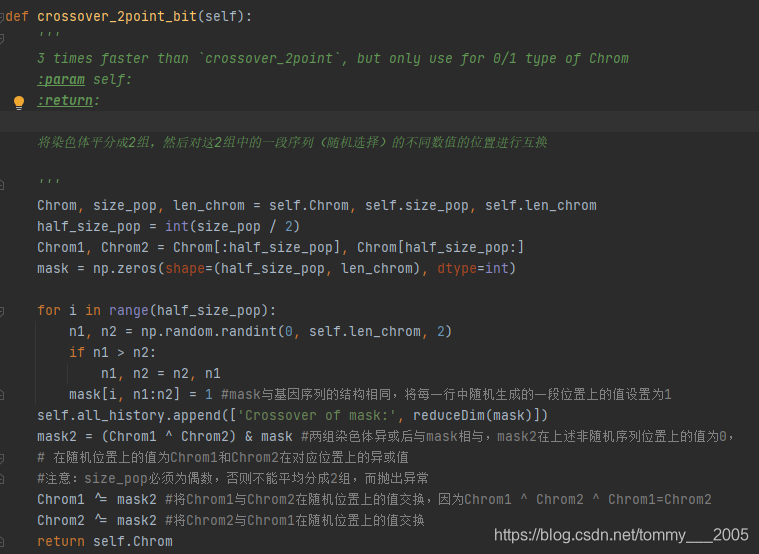
5、crossover模块的实现逻辑

交叉的思想是将染色体集合平均分成两组，对两组中每行基因序列中的随机一段进行互换。实现过程为：首先将Chrom数组从正中间那行的位置隔开形成两组染色体，然后生成交叉的位置模板mask，产生方法为从生成的与两组染色体相同shape且各元素全为0的数组中的每一行随机将一段位置的值置为1。接着将两组染色体做异或运算再与mask做逻辑与运算，产生与mask相同shape的mask2，mask2在mask的基础上，仅将随机位置上的值（为1）改变为两组染色体相互异或运算的值，其他位置的值（值为0）保持不变。最后分别将两组染色体与mask2做异或运算，得到交叉后的染色体。这两步数学逻辑为：

$Chrom1=Chrom1 \^\ mask2= Chrome1 \^\ ((Chrome1 \^\ Chrome2) \&\ mask )=\left\{\begin{matrix} Chrome1,mask=0\\ Chrome2, mask=1 \end{matrix}\right.$

$Chrom2=Chrom2 \^\ mask2= Chrome2 \^\ ((Chrome1 \^\ Chrome2) \&\ mask )=\left\{\begin{matrix} Chrome2,mask=0\\ Chrome1,mask=1 \end{matrix}\right.$

即在对应位置模板mask为1的位置上将Chrom1与Chrom2的值进行交换，为0的位置上Chrom1与Chrom2都保持不变。这样实现了在两组染色体中的每一行随机选取一段基因并将其值进行互换。

6、mutation模块的实现逻辑

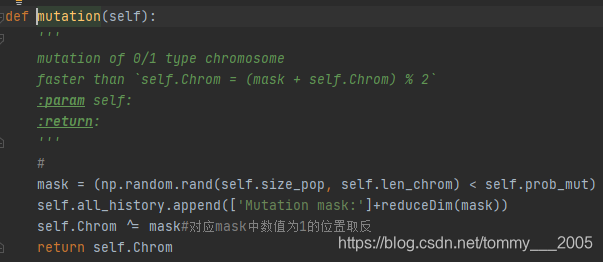
变异过程是对染色体中的基因随机进行改变。实现过程为：首先随机生成元素为[0,1)的与染色体群体Chrom相同shape的数组，然后根据该数组每个元素的值与变异因子prob_mut值进行大小比较的结果，在对应位置生成类型为布尔型的数组mask，最后将染色体群体Chrom与mask做异或运算，实质是将Chrom中对应mask为1位置上的基因值变反，得到变异后的染色体群体，即为下一代染色体群体。