吴恩达机器学习第一章作业python实现

读取数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('data/ex1data1.txt',names=['population','profit'])
print("数据前5行：",data.head(5))
print("数据后5行：",data.tail(5))
print("数据概要参数：",data.describe())
#概要数据包括平均，max，min，std等数据

用到的方法：

作用	代码
读取文件	data = pd.read_csv(file,sep,header)
显示数据	data.head/tail([null或\d+])
数据概要参数	data.describe()

pd.read_csv主要有3个参数，file,sep,header，file就是文件路径及后缀名，sep是读取格式，默认以‘，’分隔读取，案例中的txt可以看到也是使用‘，’进行分隔所以用read_csv方法并无大碍，name=[]参数是为读取的数据设置表头。

数据集准备

print("=============数据可视化===========")
data.plot.scatter('population','profit',label='population')
plt.show()
print("============改变原数据，添加一列===========")
data.insert(0,'ones',1)
print(data.head(5))
print("===========划分数据集==========")
X = data.iloc[:,0:-1]
y = data.iloc[:,-1]
print("===========数据集矩阵化==========")
X = X.values
y = y.values
#防止行列不一致后面运算报错
y = y.reshape(97,1)

用到的方法：

作用	代码
DataFrame可视化	<DataFrame>.plot.scatter(‘标题1’,‘标题2’，label=‘标签名’)
添加列数直接改变原数据	<DataFrame>.insert(loc,column,value)
DataFrame切片	X = <DataFrame>.iloc[\d+:\d+,\d+:\d+]
Dataframe矩阵化	X = <DataFrame>.values
在不更改数据的情况下为数组赋予新的形状。	<array>.reshape(n,m)

对于DataFrame类型的数据有特有的方法进行数据可视化(散点图)，
<DataFrmae>.plot.scatter('标题1','标题2'，label=‘标签名’)，再为原数据添加一列全为1的数据。<DataFrmae>.insert(loc,column,value)，loc：插入的列索引，column：插入列的标签，字符串。value：插入列的值，如果是列表那么该列表长度必须和原数据行数一致。
data.insert(0,'ones',1)为什么要为数据集新增一列全为1的新列呢？
因为矩阵的相乘必须满足第一个矩阵的列数=第二个矩阵的行数
比如有如下数据和公式：
函数h(x)
: h(x) = -40 + 0.25x

数据

2104

1416

1534

852

以上数据如果想使用矩阵去计算会发现，数据列是一个4x1的矩阵，函数系数组成的矩阵是2x1的矩阵，因此如果想要使用矩阵去计算结果，则只需在第一个矩阵中的第一列添加一列全为1的新列就行了。

编写损失函数和梯度下降算法

print("===========构造损失函数==========")
def costFunction(X,y,theta):
    inner = np.power(X * theta -y,2)
    print(inner)
    return np.sum(inner) / (2 * len(X))
#构造一个2行1列的矩阵，0填充
theta_1 = np.zeros((2,1))
print(costFunction(X,y,theta_1 ))
print("===========梯度下降==========")
def gradient(X,y,theta,alpha,irange):
    costs = []
    for i in range(irange):
        theta = theta -  np.dot(X.T,(np.dot(X,theta) - y)) * alpha / len(X)
        cost = costFunction(X,y,theta)
        costs.append(costs)
    return theta,costs

用到的方法：

作用	代码
矩阵相乘，返回一个结果矩阵	np.dot(array1,array2)

损失函数应用平均差损失函数

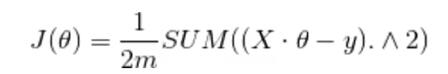
梯度下降函数：

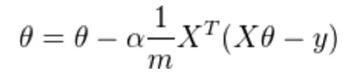
数据可视化

print("===========数据可视化==========")
fig, axc = plt.subplots(2,2)
ax = axc[0,0]
ax1 = axc[1,1]
#===========左上角图，根据给的数据绘制出的图形
x = np.linspace(data.population.min(), data.population.max(),97) #设置直线x坐标的数据集
print(type(x))
y=theta_2[0]+theta_2[1]*np.sort(data.population) #设置直线y坐标的数据集
ax.plot(x, y, 'r', label='Prediction')   #画直线
ax.scatter(data.population, data.profit, label='Traning Data')  #画点，前两个参数是点的x和y坐标的数据集
ax.legend(loc=2)    #点和线的图例，2表示在左上角。不写这句的话图例出现不了
ax.set_xlabel('Population')   #接下来设置坐标轴名称和图题
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
#===========右下角图，利用区间分割等差数列 绘制的图
x = np.linspace(data.population.min(), data.population.max(),100) #设置直线x坐标的数据集
y=theta_2[0]+theta_2[1]*x  #设置直线y坐标的数据集
ax1.plot(x, y, 'r', label='Prediction')   #画直线
ax1.scatter(data.population, data.profit, label='Traning Data')  #画点，前两个参数是点的x和y坐标的数据集
ax1.legend(loc=2)    #点和线的图例，2表示在左上角。不写这句的话图例出现不了
ax1.set_xlabel('Population')   #接下来设置坐标轴名称和图题
ax1.set_ylabel('Profit')
ax1.set_title('Predicted Profit vs. Population Size')
plt.show()

用到的方法：

作用	代码
实例化画板，2x2格式	fig, axc = plt.subplots(2,2)
构造等差数列	np.linspace(start,end,count)#开始值，结束值，元素个数

plt.subpots()用来构造一个实例化的画板，里面的参数是设置结构（2x2），将ax设置为第一行第一列的图形，我们对ax进行操作即可完成对第一个图形的绘图。ax.plot(x,y,label=)绘制直线。绘制直线就需要横纵坐标的值，**因为我们要绘制的直线是连续的值，而数据是离散的，所以我从data.population中选取[min，max]的区间去进行等差数列的分割，然后代入我们从梯度下降函数中得到的theta去获取y值，最后利用plt.plot的性质连接乘直线即可。
np.linspace(data.population.min(), data.population.max())形成在给定区间内50个元素的等差数列，然后与theta计算得出y值进行绘图。

补充学习
案例中的难点主要在于算法的编写，梯度下降函数利用迭代逐步计算出theta对应的cost最小值。不好理解，如果特征数量小于10w，则可以利用正规方程直接计算cost最小值时的theta值

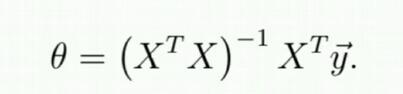
print("==========使用正规方程计算============")
def normalFun(X,y):
    theta = np.dot(np.dot(np.linalg.inv(np.dot(X.T,X)),X.T),y)
    return theta
print(">>>使用正规方程一步得出的cost：  {}".format(costFunction(X,y,normalFun(X,y))))

可以看到预测结果基本一致，使用正规方程去计算cost最小值时的参数避免了迭代，在特征数量较少（<10w）的情况下效果和效率大于梯度下降，但是在特征数量较大时（>10w），因为牵涉到矩阵的逆计算量成倍增大，此时效率不如梯度计算。