求两个正整数的最小公倍数

Java语言程序设计（基础篇）

编程综合题 6.29

求最小公倍数

编写程序，提示用户输入两个整数并求它们的最小公倍数（LCM）。
两个数的最小公倍数是指这两书的倍数中最小的数。
例如，
8和12的最小公倍数是24，
15和25的最小公倍数是75，
120和150的最小公倍数是600。
求最小公倍数的方法很多，在本练习中采用以下方法：
为求两个正整数的最小公倍数，首先为每个数创建一个素数因子表，的第一列包含所有素数因子，第二列为该数中对应素数因子出现的次数。
例如，120的素数因子为2，2，2，3，5，所以120的素数因子表如下所示：

 120的素数因子   出现次数      
      2            3             
      3            1             
      5            1

  150的素数因子   出现次数
      2            1 
      3            1
      5            2          
  两个数的最小公倍数由这两个数种出现频率最高的因子构成，所以，120和150的最小公倍数为2*2*2*3*5*5=600。其中2在120中出现了3次，3在120中出现了1次，5在150中出现了2次。
  提示： 可以用二维数组表示素数因子表，编写 getPrimeFactors(int numer)方法，使其为素数因子表返回一个二维数组。   

---

以下是我编程中的思路变化过程：

**LeastCommonMultiple1.java**

import javax.swing.JOptionPane;

public class LeastCommonMultiple1 {
    static int MAX=10;
    public static void main(String[] args) {

    //get the integers from a dialog    
        String num1=JOptionPane.showInputDialog(null,"Input","Input Dialog",JOptionPane.QUESTION_MESSAGE);

        //creat a array then initialize it ;
        int[][] primeFactorList1=new int[2][MAX];

        for(int j=0;j<primeFactorList1[0].length;j++){
            primeFactorList1[0][j]=1;
            primeFactorList1[1][j]=0;
        }

        leastCommonMultiple(Integer.parseInt(num1),primeFactorList1);

        //output the list to check      ;
        System.out.println(Integer.parseInt(num1)+" 's table of factors are");
        for(int i=0;i<primeFactorList1.length;i++){
            for(int j=0;j<primeFactorList1[0].length;j++){
                System.out.print(primeFactorList1[i][j]+" ");
            }
            System.out.println("");
        }


        String num2=JOptionPane.showInputDialog(null,"Input","Input Dialog",JOptionPane.QUESTION_MESSAGE);

        //creat a array then initialize it ;
        int[][] primeFactorList2=new int[2][MAX];

        for(int j=0;j<primeFactorList1[0].length;j++){
            primeFactorList2[0][j]=1;
            primeFactorList2[1][j]=0;
        }

        leastCommonMultiple(Integer.parseInt(num2),primeFactorList2);
        System.out.println("\n"+Integer.parseInt(num2)+" 's table of factors are");
        for(int i=0;i<primeFactorList2.length;i++){
            for(int j=0;j<primeFactorList2[0].length;j++){
                System.out.print(primeFactorList2[i][j]+" ");
            }
            System.out.println("");
        }


        //calculate the least common multiple by the two list;   that is a bug which need to fix!
        int leastCommonMultiple=1;
        for(int j=0;j<primeFactorList1[0].length;j++){
            if(primeFactorList1[0][j]==primeFactorList2[0][j]){
                if(primeFactorList1[1][j]<primeFactorList2[1][j])
                    leastCommonMultiple*=Math.pow((double)primeFactorList1[0][j], (double)primeFactorList2[1][j]);
                else
                    leastCommonMultiple*=Math.pow((double)primeFactorList1[0][j], (double)primeFactorList1[1][j]);
            }
            else{
                leastCommonMultiple*=Math.pow((double)primeFactorList1[0][j], (double)primeFactorList1[1][j]);
                leastCommonMultiple*=Math.pow((double)primeFactorList2[0][j], (double)primeFactorList2[1][j]);
            }
        }


        //output the LCM on both of console and dialog ;
        String result=String.format("\n"+leastCommonMultiple+" is the least common multiple of "+Integer.parseInt(num1)+" and "+Integer.parseInt(num2));
        System.out.println(result);
        JOptionPane.showMessageDialog(null, result);

    }


    //it is able just to handle the integer whose number of factors is less than 10, and that's why i set a const argument "MAX" which is 10 default ;  
    public static void leastCommonMultiple(int number,int[][] primeFactorList){
        int integer=number; 
        if(integer>=2){
            for(int factor=2;factor<=integer;factor++){
                if(integer%factor==0){
                    //load into the factor list;
                    updatePrimeFactorList(factor,primeFactorList);
                    integer=integer/factor;
                    //System.out.print(factor+" ");
                    leastCommonMultiple(integer,primeFactorList);
                    break;
                }
                //the following "else" is not essential,it may not miss somewhere
                else 
                    continue;
            }
        }
//      else 
//          JOptionPane.showMessageDialog(null, "the number you put is not valid!","Error",JOptionPane.INFORMATION_MESSAGE);

    }

//update the prime factors list ;
    public static void updatePrimeFactorList(int num,int[][] primeFactorList){
        for(int j=0;j<primeFactorList[0].length;j++){
            if(primeFactorList[0][j]==num){
                primeFactorList[1][j]++;
                break;
            }
            else if(primeFactorList[0][j]==1){
                primeFactorList[0][j]=num;
                primeFactorList[1][j]=1;
                break;
            }
            else 
                continue;
        }
    }
}

Result of test :



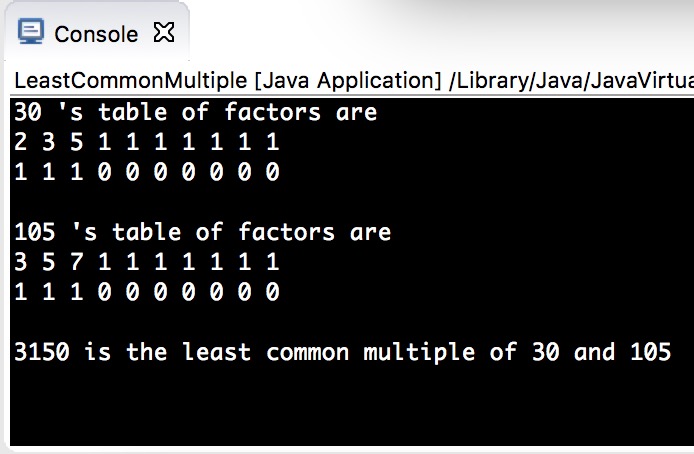
从输出这里你可以看到我采用的是二维数组primeFactorList:int[2][MAX]的形式存储整数的素数因子表，primeFactorList[i][0]存放素数因子，相应的 primeFactorList[i][1]存储相应素数因子出现的次数，并且开始用1初始化 primeFactorList[i][0],用0初始化 primeFactorList[i][1]。

**Bugs** - **很显然，如上图输出结果所示，在素数因子表里面存在着我们编程方式留下 痕迹，