数据结构--循环链表

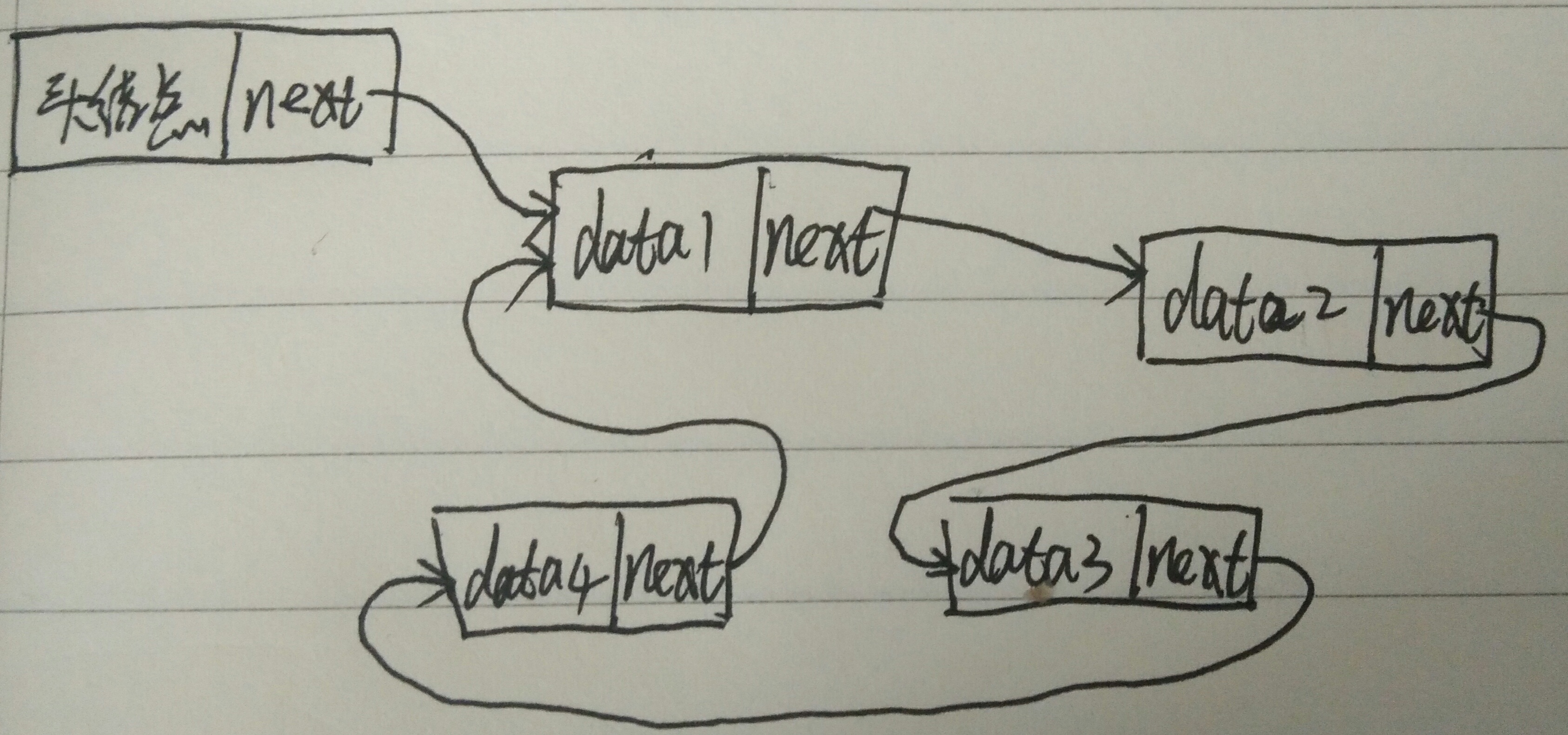
概念上的循环链表是任何数据元素都有一个前驱和一个后继，首结点的前驱是尾结点，尾结点的后继是首结点，所有数据元素的关系在逻辑上构成一个环，而单链表是除了首尾数据结点外都有前驱和后继。

实现上循环链表是一种特殊的单链表，在尾结点的指针域中保存了首结点的地址。

如图所示：

实现设计思路：

通过类模板实现。

继承自LinkList类。

定义指向最后一个结点的函数。

定义首尾相连的函数。

特殊处理在第0个结点位置的插入和删除操作。

重新实现清空和查找、遍历操作。

插入位置为0时：

头结点和尾结点均指向新结点。

新结点成为首结点插入链表。

删除位置为0时：

头结点和尾结点指向当前位置为1的结点。

保证异常安全的前提下销毁首结点。

类模板声明及定义：

template <typename T>
class CircleList : public LinkList<T>
{
  protected:
    typedef typename LinkList<T>::Node Node;

    int mod(int i)const//取余操作
    {
        return (this->m_length == 0) ? 0 : (i % this->m_length);
    }
    Node* last()const//指向最后一个数据结点
    {
        return this->position(this->m_length - 1)->next;//倒数第二个的下一个就是最后一个
    }
    void last_to_first()const//首尾结点连接起来
    {
        last()->next = this->m_header.next;
    }

public:
    bool insert(const T& e)
    {
        return insert(this->m_length,e);
    }

    bool insert(int i, const T& e)//插入操作
    {
        bool ret = true;
        i = i % (this->m_length + 1);//计算出需要插入的位置
        ret= LinkList<T> :: insert(i,e);//调用父类成员函数

        if(ret && (i == 0))//特殊处理插入位置为0的情况
        {

            last_to_first();
        }

        return ret;
    }

    bool remove(int i)
    {
        bool ret = true;
        i = mod(i);

        if(i == 0)特殊处理删除位置为0的结点
        {
            Node* toDel = this->m_header.next;//保存首结点
            if(toDel != NULL)
            {
                this->m_header.next = toDel->next;//头结点连接1号结点
                this->m_length--;
                if(this->m_length > 0)//判断是否只剩下一个结点
                {
                    last_to_first();
                    if(this->m_current == toDel)
                        this->m_current = toDel->next;
                }
                else
                {
                    this->m_header.next = NULL;
                    this->m_current = NULL;
                }
                this->destroy(toDel);//异常安全
            }
            else
            {
                ret = false;
            }
        }
        else
        {
            ret = LinkList<T>::remove(i);
        }
        return ret;
    }

    bool set(int i,const T& e)//调用父类set函数
    {
        return LinkList<T> :: set(mod(i),e);
    }
    T get(int i)const//调用父类get函数
    {
        return LinkList<T>::get(mod(i));
    }
    bool get(int i, T& e)const//此处实现和视频不同，视频在T&前加了const
    {
        return LinkList<T> :: get(mod(i),e);
    }

    /*
    *一开始提到的利用LinkList的find函数查找，先last指向NULL，再find，最后last_to_first，这样是不可靠的，当find里的比较操作符
    * 重载时抛出异常后，就会返回异常，最后链表状态也被改变了，成为了一个单链表
    */
    int find(const T& e)const
    {
        int ret = -1;//没找着
        Node* slider = this->m_header.next;
        for(int i = 0; i < this->m_length; i++)
        {
            if(slider->value == e)
            {
                ret = i;
                break;
            }
            slider = slider->next;
        }

        return ret;
    }

    /*
    *不能使用先将首节点指向NULL再LinkList<T>:: clear()
    * 当clear()抛出异常后就改变了链表状态
    */
    void clear()
    {

        while(this->m_length > 1)
        {
            this->remove(1);//remove(1)的好处是避免了使用remove(0)从而执行大量语句，拉低效率
        }
        if(this->m_length == 1)
        {
            Node* toDel = this->m_header.next;

            this->m_header.next = NULL;
            this->m_length = 0;
            this->m_current = NULL;

            this->destroy(toDel);//异常安全
        }
    }

    bool move(int i, int step)
    {
       return  LinkList<T> :: move(mod(i),step);
    }

    bool end()
    {
        return (this->m_length == 0) || (this->m_current == NULL);
    }
    ~CircleList()
    {
        clear();
    }

};

注意：由于CircleList是LinkList的子类，当独立使用CircleList时就只调用子类的实现版本，所以将LinkList类的所有成员函数做成虚函数。

程序段中有关父类的调用请参考单链表LinkList类的实现。

测试题：约瑟夫换问题

已知n个人(以编号0，1,2,3.....n-1分别表示) 围坐在一张圆桌周围。从编号为k 的人开始报数，数到m 的那个人出列; 他的下一个人又从1开始报数，数到m 的那个人又出列; 依此规律重复下去，直到圆桌周围的人全部出列。

用循环链表实现如下：

void josephus(int num, int start, int step)//总数为num，从第start个开始，每数step个数出列
{
    CircleList<int> c1;

    for(int i = 1; i <= num; i++)
    {
        c1.insert(i);
    }

    c1.move(start-1, step-1);//每移动m-1次就可以到达目的，如三个一循环只需移动两个就能让第三个出列。

    while(c1.length() > 0)
    {
        c1.next();
        cout << c1.current() << endl;
        c1.remove(c1.find(c1.current()));
    }
}

在main里调用并输出：

3
6
1
5
2
8
4
7