数据结构--双向链表

单链表的单向性：只能从头结点开始高效访问链表中的数据元素。

单链表还存在另一个缺陷：逆序访问时候的效率极低。

如下：

    LinkList<int> list;

    for(int i = 0; i < 5; i++)
    {
        list.insert(0,i);
    }
    
    for(int i = list.length() - 1; i >= 0; i--)
    {
        cout << list.get(i) << endl;
    }

根据大O推算法可以得出一个for循环的时间复杂度为O(n)，get(i)的时间复杂度也是O(n)，所以一个逆序访问数据的时间复杂度为O(n^2)，所以效率是极低的。

所以新的需求来了，我们需要一种线性表能够高效逆序访问数据。在单链表的结点基础上增加一个指针域pre，它指向上一个结点，即前驱结点。

   

我们称之为双向链表。

那么双向链表的继承层次结构是什么？由于它和单链表的数据结点的结构不同，所以它的继承层次为继承自List类。

通过类模板实现双向链表。

模板实现声明如下：

    template <typename T>
    class DualLinkList : public List<T>
    {
    protected:
        struct Node : public Object
        {
            T value;
            Node* next;
            Node* pre;

        };
        //mutable Node m_header;//分析下面的匿名结构的作用：本质上就是防止调用创建T value对象时调用构造函数，下面的匿名结构在内存布局上和Node m_header布局相同
       mutable struct : public Object//如果未继承自Object可能导致内存布局和Node m_header内存布局不同。
        {

            char reserved[sizeof(T)];
            Node* next;
            Node* pre;

        }m_header;
        int m_length;

        int m_step;//保存游标移动的次数
        Node* m_current;//游标

        Node* position(int i)const//用于定位 ，优化insert、remove、get、set函数用，但是本文件未优化，便于复习使用，这里只是说明可以优化
        {
            Node* current = reinterpret_cast<Node*>(&m_header);

            for(int p = 0; p < i; p++)
            {
                current = current->next;
            }
            return current;
        }
        virtual Node* create()
        {
            return new Node();
        }
        virtual void destroy(Node* pn)
        {
            delete pn;
        }
    public:
        DualLinkList();
        bool insert(int i,const T& e);
        bool insert(const T& e);
        bool remove(int i);
        bool set(int i,const T& e);
        bool get(int i,T& e )const;
        virtual T get(int i)const;
        int  find(const T& e )const;//返回的是查找到的结点的位置
        int length()const;
        void clear();
        virtual bool move(int i, int step = 1);
        virtual bool end();
        virtual  T current();
        virtual bool next();
        virtual bool pre();
        ~DualLinkList();

};

在模板类中只需要实现一些关键操作，如insert、remove、clear、pre操作，其余的都和LinkList的实现完全相同。

一、插入

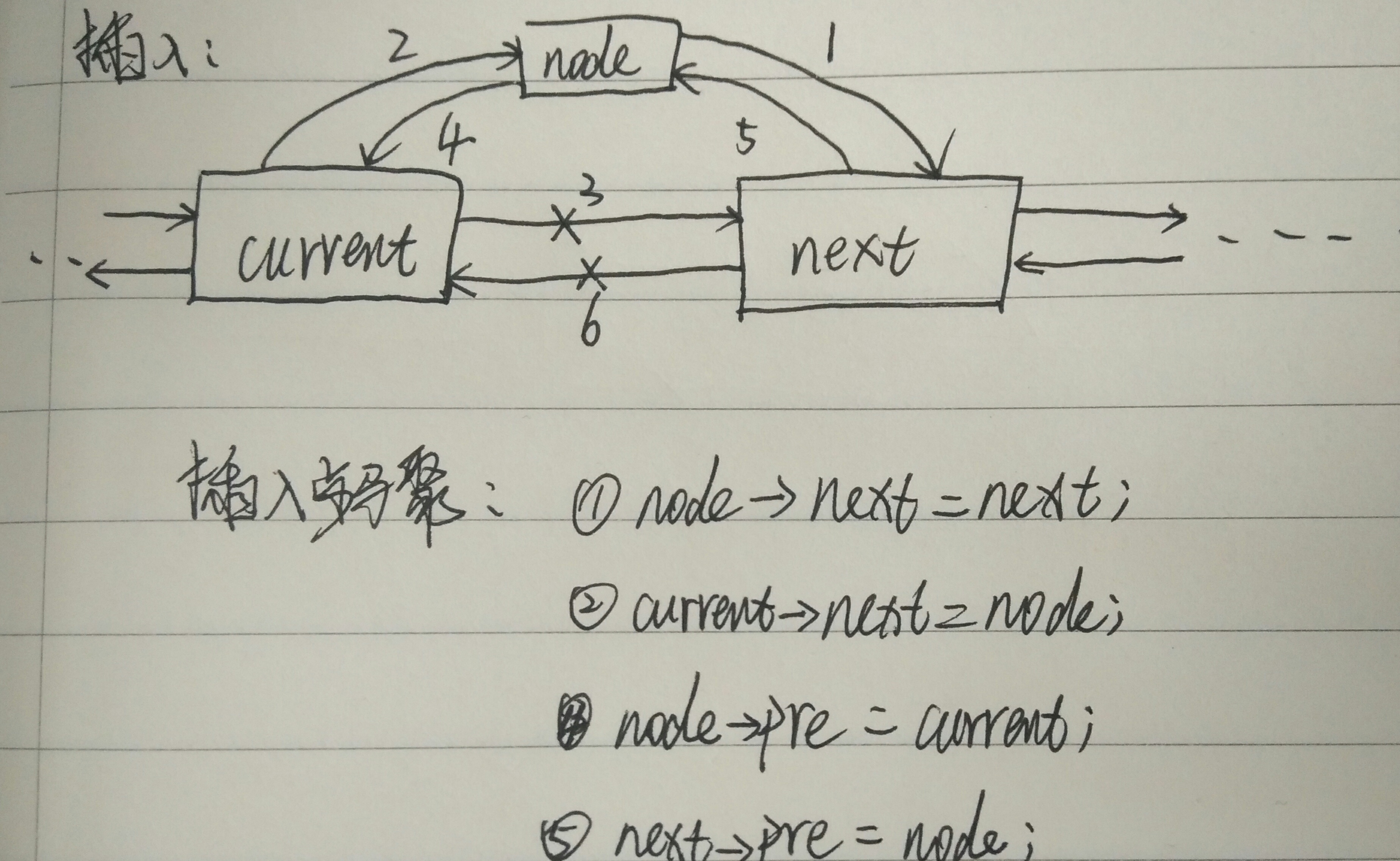
插入操作的原理本质上和单链表是一样的，只是多了连接前驱指针的步骤，具体步骤如下图：

实现代码如下：

bool insert(int i,const T& e)
        {
            bool ret = (i >= 0) && (i <= m_length);

            if(ret)
            {
                Node* node = create();

                if(node != NULL)
                {

                    Node* current = reinterpret_cast<Node*>(&m_header);

                    //定位到要插入的位置
                    for(int p = 0; p < i; p++)
                    {
                        current = current->next;
                    }

                    Node* next = current->next;
                    node->value = e;

                    //连接next域
                    //第一二步
                    node->next = next;
                    current->next = node;

                    //连接pre域
                    //第三四步
                    if(current != reinterpret_cast<Node*>(&m_header))
                    {
                        node->pre = current;
                    }
                    else
                    {
                        node->pre = NULL;
                    }
                    if(next != NULL)
                    {
                        next->pre = node;
                    }

                    m_length++;

                }
                else
                {
                    THROW_EXCEPTION(NoEnoughMemoryException,"No memory to new ");
                }
            }

            return ret;
        }

        bool insert(const T& e)
        {
            return insert(m_length,e);
        }

实现步骤就是如图步骤所示，需要注意的是插入的位置为首结点时pre域应该为NULL，当next结点不指向NULL时pre域才有效。

最后实现了插入重载函数，每次插入末尾位置。

二、删除

删除操作也需要对pre域进行连接，先将链表连好，最后销毁需要删除的结点。

如图：

实现如下：

        bool remove(int i)
        {
            bool ret = (i >= 0) && (i < m_length);

            if(ret)
            {
                Node* current = reinterpret_cast<Node*>(&m_header);

                for(int p = 0; p < i; p++)
                {
                    current = current->next;
                }

                Node* toDel = current->next;
                Node* next = toDel->next;

                if(m_current == toDel)//作用：在遍历中执行remove操作时删除结点后会导致m_current指向不变，从而使m_current->value为随机值，所以当需要删除将m_current指向下一个结点
                {
                    m_current = next;
                }

                //第一步
                current->next = next;
                //第二步
                if(next != NULL)
                {
                    next->pre = toDel->next;//出过BUG，原先写法：next->pre = current;
                }

                m_length--;//保证异常安全，因为当销毁数据时抛出异常（结点是类类型，并且在析构函数中抛出异常）先长度减一再销毁结点

                destroy( toDel );

            }
            return ret;
        }

具体实现在图中已有说明，程序是按照图中步骤进行的。同样需要注意的是next不为NULL时pre域才有效。

三、清空

实现原理是每次删除首结点，直到链表长度为0。

四、前移

单链表中实现了向后移动的操作，在双向链表中也添加相似的功能函数，实现如下：

        virtual bool pre()
        {
            int i = 0;
            while((i < m_step) && (!end()))
            {
                m_current = m_current->pre;
                i++;
            }

            return (i == m_step);
        }

基本操作就这些，在声明中还有一些函数并没有实现，因为它们和单链表中的实现完全一样，具体实现请参考前面的文章“单链表实现”。且构造函数和析构函数的函数体几乎一样，只不过构造函数中需要初始化pre指针。

小结：

双向链表是为了弥补单链表缺陷而设计的。

在概念上，双向链表不是单链表，所以没有直接继承关系。

双向链表中的游标能够直接访问当前节点的前驱和后继。

双向链表是线性表概念的最终实现（更贴近理论上的线性表）。