关于博弈树的历史启发

最新推荐文章于 2025-04-02 13:52:06 发布

trancybao

最新推荐文章于 2025-04-02 13:52:06 发布

阅读量1.3k

点赞数 2

分类专栏：人机博弈文章标签：人机博弈历史启发象棋 QT

本文链接：https://blog.csdn.net/trancybao/article/details/103663218

版权

人机博弈专栏收录该内容

1 篇文章

订阅专栏

最近研究棋类博弈程序中，参考PC游戏编程（人机博弈）这本书时，看到历史启发这种优化思路，但却难以理解，搜索别人的讲解却发现只是摘抄了概念，现在谈谈自己的理解，希望对后来人有些帮助。

一、概念

ALPHA-BETA 搜索的剪枝效率，几乎完全取决于节点的排列顺序。在节点排列顺序处于理想状态的情况下， ALPHA-BETA 搜索需遍历的节点数仅为极大极小算法所需遍历的节点数的平方根的两倍左右。也就是说对一棵极大极小树来说，如果极大极小搜索需遍历 10^6 个节点求得结果，那么处于理想状态的ALPHA-BETA搜索仅需遍历约2000个节点就可求得结果。而在节点的排序最不理想的情况下， ALPHA-BETA搜索要遍历的结点数同极大极小算法一样多。如何调整待展开的走法排列的顺序，是提高搜索效率的关键。根据部分已经搜索的结果来调整将要进行搜索的节点顺序是一个可行的方向。通常一个局面经搜索得知较好时，在其后继节点当中往往有一些相似的局面，比如仅有一些无关紧要的棋子位置不同等等。这些相似的局面往往也是较好的。可以通过一些较复杂的判断来找出这些相似的局面，率先搜索，从而提高剪枝效率。但这一方法需要具体棋类相关的知识，并且往往判断复杂而效果不佳。

J.Schaeffer提出了History Heuristic的方法，避免了对具体棋类信息的依赖。

Alpha-Beta搜索中一个好的搜索算法可定义为:

由其产生的节点引发了剪枝
未引发剪枝，但是是其兄弟节点中的最佳节点

在搜索的过程中，每当找到一个好的走法，就将与该走法相对应的历史得分作一个增量，一个多次被搜索并确认为好的走法的历史纪录就会较高，当搜索中间节点时，将走法根据其历史得分排列顺序，以获得较佳的排列顺序。这比采用基于棋类知识而对节点排序的方法要容易得多。由于历史得分表随搜索而改变，对节点顺序的排列也会随之动态改变。

二、尝试用排序对Alpha-Beta剪枝优化

为了更好地理解历史启发，我们先尝试自己对搜索树优化。Alpha-Beta剪枝对于节点的排列的顺序是很敏感的，这个很容易理解，因此首先想到如果进行搜索前就直接给节点排序，结果会怎样呢，做法很简单，将每步拿出来走一下，计算局面价值，这个价值作为每步的价值，再撤回这步，然后根据每步价值排序。

伪代码如下：

计算所有可能棋路存入possibleSteps；

遍历possibleSteps{

尝试走一步possibleSteps[i];

possibleSteps[i]->value=当前局面价值;

撤回possibleSteps[i];

}

根据possibleSteps[i]->value对possibleSteps排序;

做了这样的事情后，我们来看看会发生什么。

将搜索层数设为5，红棋先走，依次走炮、兵、马

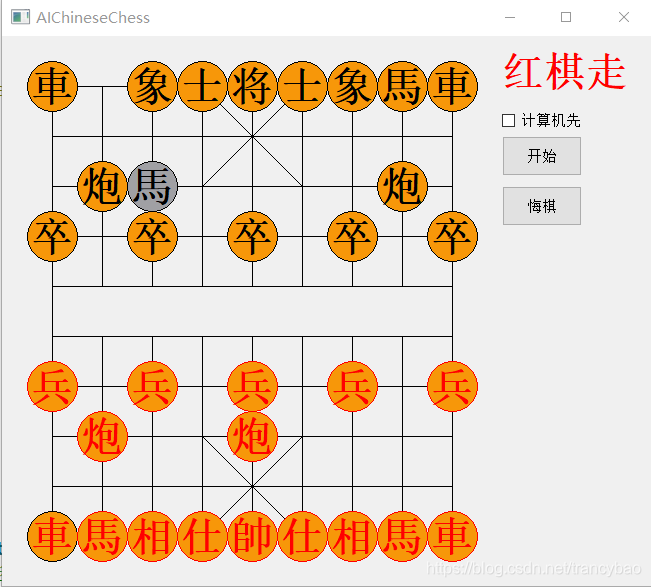
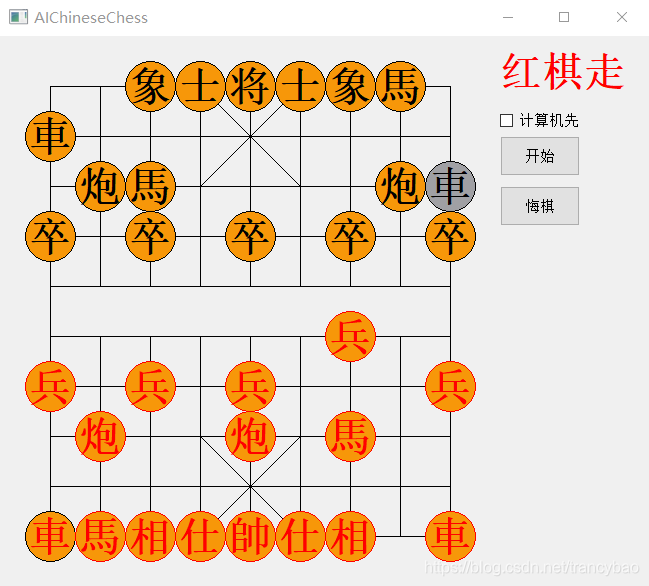
以上是红棋走一步后黑棋的应对，打印出每步遍历的节点数，调用评估函数次数，耗费时间，如下表

可以看出排序后遍历节点数大大减少，但是耗费时间却增加了，原因是排序时频繁调用了评估函数，而评估函数是很耗费时间的，因此这个思路行不通，但是印证了节点的顺序对Alpha-Beta剪枝的效率有很大的影响，并且对最终抉择没有影响。

三、利用历史记录对节点排序

提前计算棋路对节点排序行不通，因为做了很多重复的调用评估函数的过程，那我们想想，有没有其它途径可以得到每个棋路的价值呢，我们可以注意到，每次遍历的节点中其实有很多是重复的，例如車进了一位，下一次飞象，下次遍历到車进了两位时，依然要遍历飞象这一步，这两次飞象的价值其实是接近的，同样的道理，如果我们找到了一个好的棋路（前面已经有定义），那么在接下来的遍历中，它大概率也是一个好的棋路，如果多次遍历都得出出它是一个好的棋路，那么大概率它真的就是一个好的棋路。

我们在遍历的过程中每遇见一次给这些好的棋路加一个权值，那么下一次遍历就可以根据权值对所有的节点排序，问题在于，我们如何保存这些棋路供下次查找使用呢，很容易想到一个动态数组，遍历到一个好的节点就放进去，下次遍历时首先查表，出现几次就加上权值的几倍，没有出现就是0，计算possibleSteps中每步的价值，然后排序，再进行搜索，但实际操作很容易发现这种方法非常慢，原因是随着搜索的进行，表的容量会急剧上升，查表耗费的时间会急剧上升，导致效率很低。

四、静态表记录节点价值

既然动态表不行，那么用静态表呢，静态表的存取效率很高，把所有走法存在静态表里，一个一个对应，能不能行呢？乍一看，这得占用多大的空间啊，应该行不通吧，但仔细想想，一个車的所有可能走法有多少个呢，90*90个，（0,0）->(1,0) (0,0）->(2,0) (0,0)->(3,0) ……，就是棋盘中每个点到另一个点的集合，棋盘共90个点，因此是90*90。我们只需要在对应的90*90的二维数组中填入每步的得分就行了，因此占用空间是90*90*4B，4B是一个int数据占用的空间，也并不大，对于现在的计算机内存来说。既然能行，那么我们想有32个棋子，是不是要对应32张表呢，但是我们会发现书上只用了一张表，这时候就不得不感叹大佬的智慧了。

实际上，对于每一个局面来说，只需要起始坐标和终点坐标就可以对应一个棋子，而不需要判断棋子类型，例如从(0,1)->(2,2)(看上面的棋盘)，这个棋子就是左边的黑马，而不会是其它棋子，或许你会怀疑，这是多步估计，那么后面有可能出现另一匹马走过这个位置，确实有可能如此，但是那又如何呢，我们找的是一步好棋，而不是最佳的棋，这样的情况我们可以暂且忽略不管。我们根据坐标起始和终点位置就可以判断棋子类型。下面给出棋路和静态表的对应关系：

棋盘从左往右扫描，设定HistoryScore[90][90]，Step的数据结构是

Class Step{

...

int x_From;

int y_From;

int x_To;

int y_To;

...

}

则Step对应HistoryScore[Step.y_To*9+Step.x_To][Step.y_From*9+Step.x_From]，则可以将每步棋和HistoryScore表对应。

五、历史启发的具体实现

定义HistoryScore类：

class HistoryScore
{
public:
    HistoryScore();
    int HistorySore[90][90];//历史记录表

    void resetHistoryScore();//重置历史记录表
    void addHistoryScore(Step*,int);//添加历史记录
    void sortPossibleSteps(QVector<Step*>&);//排序可能的步数

};

实现部分：

//重置历史记录表
void HistoryScore::resetHistoryScore(){
    for(int i=0;i<90;i++){
        for(int j=0;j<90;j++){
            HistorySore[i][j]=0;
        }
    }
}

//加入历史记录表，根据Step和所处深度计算价值
void HistoryScore::addHistoryScore(Step *step,int depth){
    //横向扫描
    //求列
    int i=Step.y_To*9+Step.x_To;
    //求行
    int j=Step.y_From*9+Step.x_From;
    HistorySore[i][j]+=(int)qPow(2,double(depth));
}

//根据历史记录表对所有可能的步数排序
void HistoryScore::sortPossibleSteps(QVector<Step *> &possibleSteps){
    QVector<Step*>::iterator iter;
    for(iter=possibleSteps.begin();iter!=possibleSteps.end();iter++){
        (*iter)->step_value=HistorySore[(*iter)->x_From*10+(*iter)->y_From][(*iter)->x_To*10+(*iter)->y_To];
    }
    std::stable_sort(possibleSteps.begin(),possibleSteps.end(),cmpSteps);//从大到小排序
}

这里加的权值是J.Schaeffer建议的2^depth，离叶子节点越近则越小，可以理解为越上面的节点是经过更多次计算挑选的，所以价值越大（不一定准确）。

六、历史启发效果

在Alpha-Beta中加入历史启发，再进行三步走棋，效果如下：