平方和的几何解释

平方和的几何解释

高斯小时候被老师问到$1+2+\cdots +99+100$的和，聪明机智的高斯几乎脱口而出5050。在我们现在看来其实很简单，也就是一个等差数列的求和公式而已：

$$\sum_{i=1}^ni = \frac {n (n+1)} 2$$ 一般地，如果等差数列{ $a_i$}的公差为d，则： $$\sum_{i=1}^n a_i = \frac {n (n+1) d} 2$$

在数学中，我们经常会用到平方和的公式，但是，平方和的公式不是并非如等差数列的求和公式那般直观。因此，若想对平方和公式有更加深入的理解，几何解释是个不错的选择。

$$\sum_{i=1}^n i^2 = \frac 1 3 n (n+1) (n+\frac {1} {2} )$$

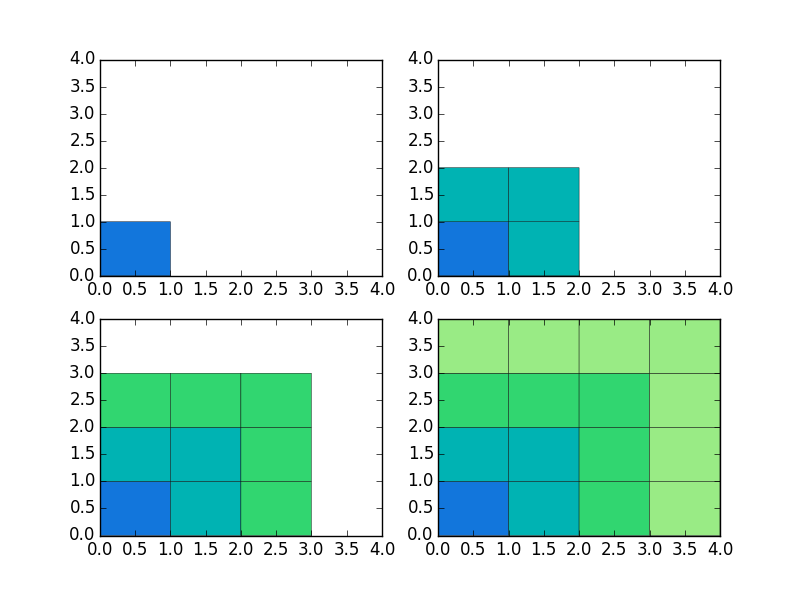
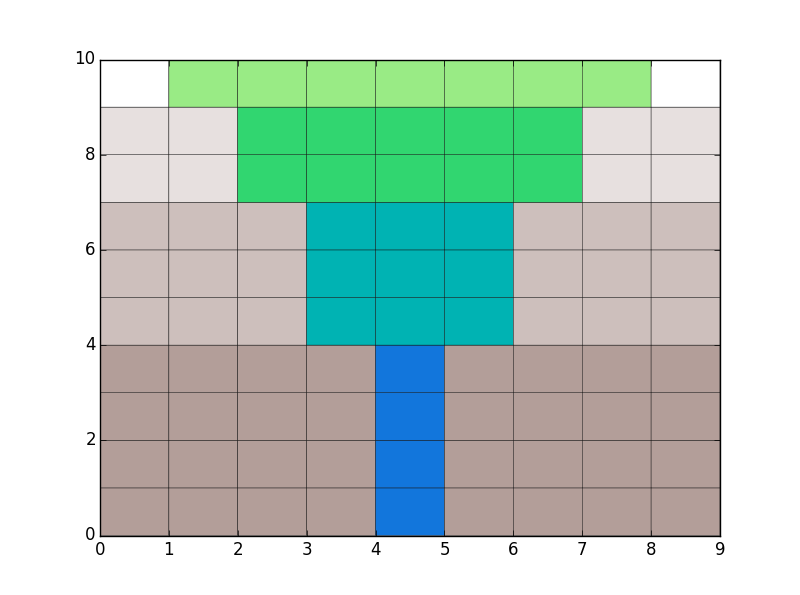
不失一般性，我们选取n=4来对平方和公式作几何解释。如下左图所示，我们将每个平方项表示成一些方块，然后我们将左图中的方块在右图中展开：

细心观察图1和图2的联系，我们看到图2中间部分就是图1的那些方块，因此方块数就是$1^2+2^2+\cdots+n^2$个，不仅如此，我们细心地分别看图2的左右两部分，可以明显地看出，两边的方块数都是$1^2+2^2+\cdots+n^2$个。又，图二总的方块数为$(2n+1)\times (1+2+\cdots +n)$，聪明的高斯又告诉我们：$(1+2+\cdots +n) =\frac {n(n+1)} 2$
所以，综合上面的式子，我们有：

$$\begin{align} 3\sum_{i=1}^n i^2 & = (2n+1)\times (1+2+\cdots +n)\\ & = (2n+1) \frac {n(n+1)} 2 \\ & = (n+\frac {1} {2} )(n+1)n \end{align}$$
即：
$$\begin{align} \sum_{i=1}^n i^2 & =\frac 1 3 n(n+1)(n+\frac {1} {2} ) \end{align}$$

得证。现在，我们只要能记得上述二图， 就再也不会忘记平方和公式了。

注 ：更多平方和的几何解释，详见:正整数的平方和公式是什么？怎么证明？

附 ：python图代码

import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
from numpy.random import rand
import numpy as np

C = np.zeros([4,4])
fig2 = plt.figure()
for i in range(4):
    for j in range(i+1):
        C[i,j] = C[j,i] = 0.1 * (i+1)
# C[0,0] = 0.1
# C[1,0] = C[0,1] = C[1,1] = 0.2
# C[2,0] = C[0,2] = C[1,2] = C[2,1] = C[2,2] = 0.3
# C[3,0] = C[0,3] = C[1,3] = C[3,1] = C[3,2] = C[2,3] = C[3,3] = 0.4
for i in range(1,1+4):
    plt.subplot(2,2,i)
    plt.pcolor(C[:i,:i],norm=mcolors.NoNorm(),cmap='terrain',edgecolors='k',linewidths=0.3)
    plt.axis([0,4,0,4])
plt.show()


n = 4
block_rows = n
now_row = 0
A = np.zeros([n*(n+1)/2, 2*n+1])
for i in range(n): # i遍历n个blocks
    for block_row in range(block_rows): # block_row遍历一个block的所有行
        for k in range(2*n+1): # k遍历一行的所有单元格
            if k in range(n-i,n+i+1):
                A[now_row,k] = 0.1*(i+1)
            else:
                A[now_row,k] = 0.8+0.05*(i+1)
        now_row += 1
    block_rows -= 1

plt.pcolor(A,norm=mcolors.NoNorm(),cmap='terrain',edgecolors='k',linewidths=0.3)
plt.show()