1000瓶水里有1瓶毒药，10只老鼠能试出来吗？

今天在网上看到一道题，据说是微软的测试题

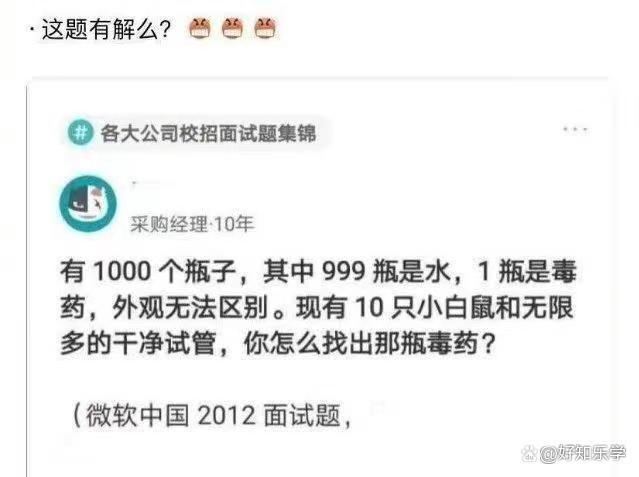
当然能，只要1只老鼠就够了，让它一瓶一瓶地试，直至试出毒药。

不过，我们也要考虑效率，是不是？比如，毒药是1小时后才发作，那怎样用最短的时间来找出毒药？

我们的目标就是，不算配药的时间，1小时搞定。

学过的朋友，直接用结论就可以算出。

没学过的朋友，就让我们一起用数学家的思维方式来探究这道题。

一、从少到多，从简到繁

（1）先从1只老鼠开始，最多可以试几瓶？

 

1号瓶有毒，则1号鼠毒死。

2号瓶有毒，则1号鼠活着。

小结：

此方法，可得出一个重要思路，最后一瓶空着，不需要老鼠试药，如果有老鼠毒死，此瓶无毒；如果其他老鼠都活着，此瓶有毒.

（2）2只老鼠呢？先想想

3瓶？

别急着下结论，看看能不能再加一瓶？看下图

是不是很有意思？

1号鼠和2号鼠都试3号瓶，如果2只都毒死，才能说明3号有毒；

反之，只有1只死了，或2只都没死，则3号无毒。

小结：

这又给了我们一个启示：可以让2只老鼠，都试一瓶相同的水，如果这2只鼠都被毒死了，说明这瓶有毒；反之，此瓶无毒。

归纳目前得到的结论，猜想3只老鼠最多可以试几瓶？

6瓶？ 8瓶？

2组数据不形成规律，我们继续！

（3）3只老鼠最多可以试几瓶？

根据前面总结的

结论1：最后一瓶空着。

结论2，让2只老鼠试相同的一瓶。

可我们得到如下方法。

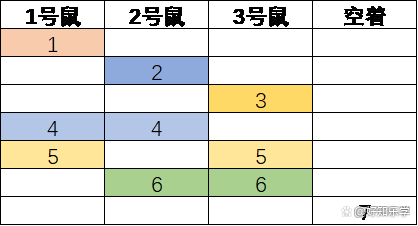
居然既不是6瓶，也不是8瓶，而是7瓶！这怎么回事？

我们先观察、分析。

1，2，3号瓶，都是只给1只老鼠吃。

4，5，6号瓶，都是同时给2只老鼠吃。

那………，我们是不是可以弄一瓶同时给3只老鼠吃？

如果3只老鼠都死了，不就说明这瓶有毒吗？

对方法进行改进，如下图，是8瓶！

原来的结论2：让2只老鼠试相同的一瓶。

拓展为：可以让n只老鼠试相同的一瓶。

看，我们在尝试中，不停地总结和归纳。是不是有点数学家的思维方式了？

总结当前的结论

二、分析、归纳：

聪明的朋友是不是很快归纳出规律了？

10只老鼠，最多可以试1024瓶，那1000瓶当然可以试出来了。

推理到这一步，对大部分人来说，已经足够了。尤其对小学生而言，能进行这样的推理已是相当不错了，是佼佼者了

三、深入探究

我们继续探究，尝试用定理或公式来推导验证，使结论在逻辑上更加严谨。

首先回顾前面的过程！回到3只老鼠的方法图

根据公式

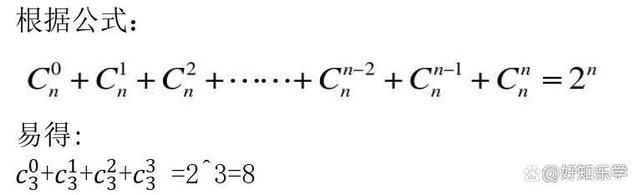
如果再增加1瓶，这1瓶，给1只老鼠、2只老鼠、3只老鼠试药，都会出现和原来重复的组合，导致无法区分。因此不能再增加。因此8瓶是最大的。

依照这个方法再计算10只老鼠:

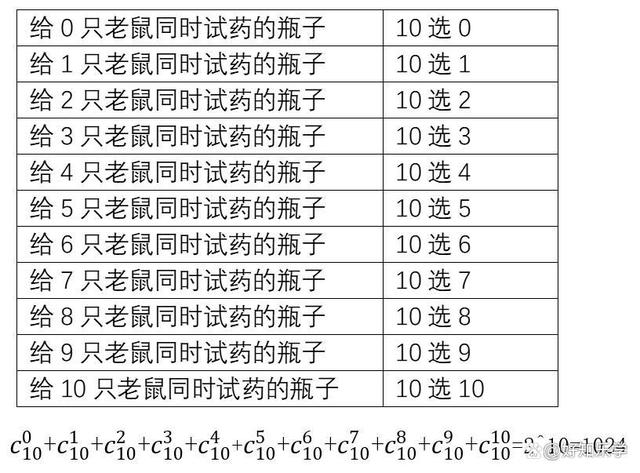
N只老鼠，同理可证。

四、拓展应用——二进制编码

以3只老鼠举例。把这个图稍微变动一下，将瓶子的编号清空，只留下颜色。

涂色表示给老鼠试药，空白表示不试。

现在开始重新编号，将图中的涂色部分用的“1”表示，空白部分用“0”表示，再将二进制改成对应的十进制。

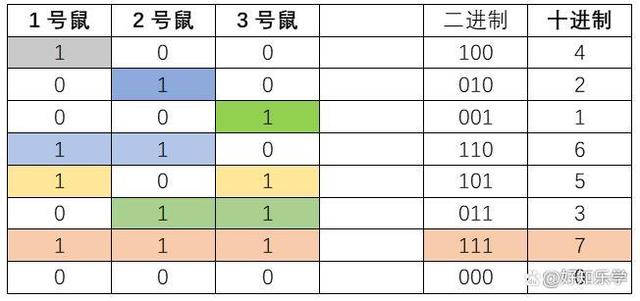
需要用到的二进制编码是“000~111”，对应的十进制编码是0~9，正好一共8个。

下面，我们再换个角度来分析，

假如我们给每只老鼠都有选择的权利，老鼠也不知道这是毒药还是糖水，把1瓶药水拿到10只老鼠的面前，让它们自由选择，它可以选择喝或者不喝。

喝记为“1”，不喝记为“0”，就这两种情况。10只老鼠，每只老鼠都有2种选择。

根据计数原理。很容易知道，一共有2^10=1024种选择情况，就是可以试1024瓶药水。

什么？你说如果选择情况出现雷同怎么办？那就让它重选，直到不重复为止！

比如，我们把1瓶药水拿到10只老鼠的面前，2号鼠，5号鼠，9号鼠“自由”选择了喝，其他老鼠没有选择。

对应的二进制编码为：0100100010，转换成十进制就是290。我们就知道290号药瓶，是哪些老鼠在试药了。

二进制编码从0000000000到1111111111，对应的十进制编号为0~1023，一共1024个。

二进制编码，最妙的用处在于，可以对每瓶进行编号，可以清楚地知道每一瓶是给了哪些老鼠尝试的，也更加方便于计算机编程使用。

---

结束