四次方程S4群的伽罗瓦分解

a,b,c,d是一般四次方程的四个根，对应S4的伽罗瓦分解如下图所示：

24个置换中有六个值，这六个值恰好对应S3，生成元是翻转和旋转b,c,d,如下图所示：

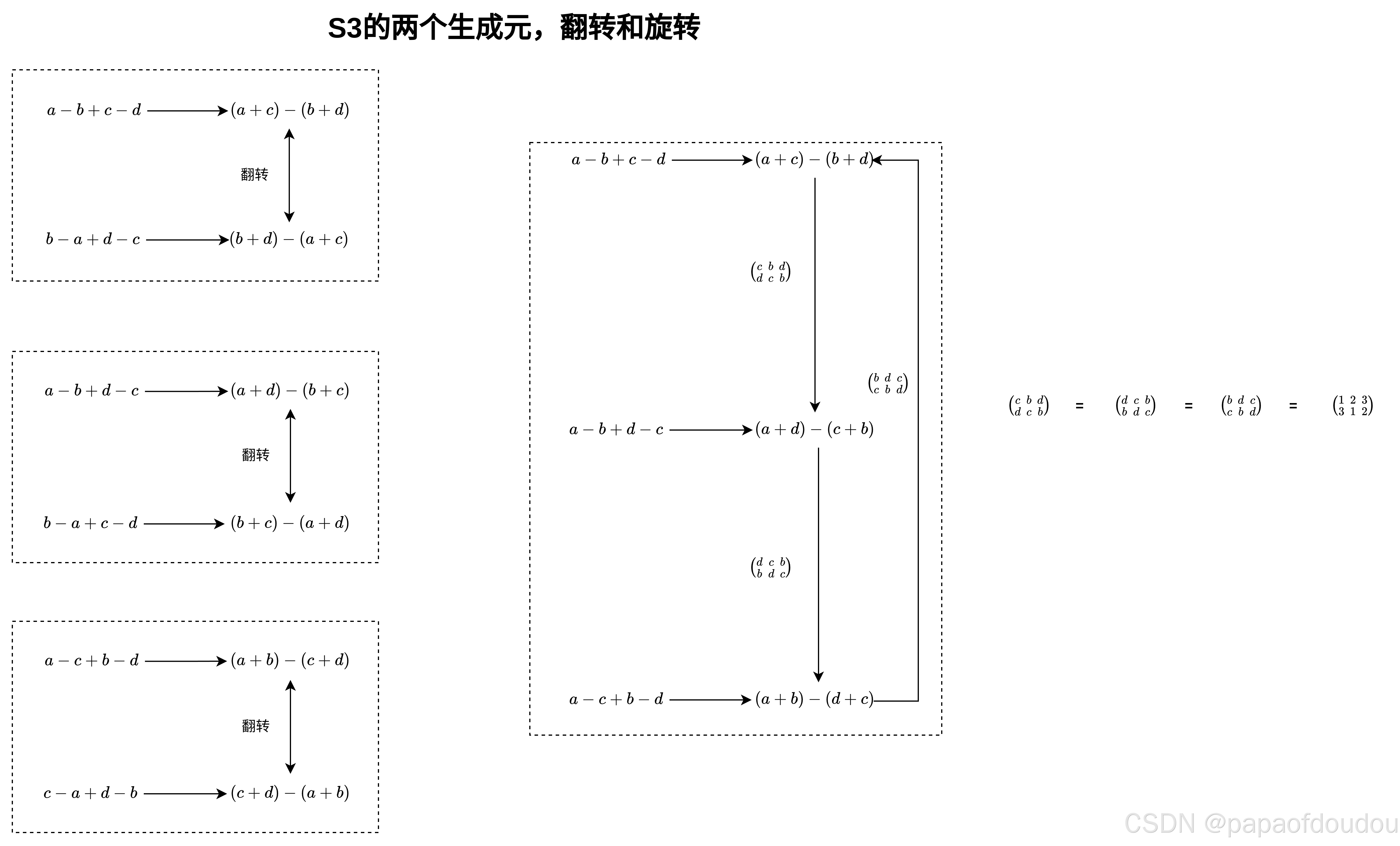
也就是说，S4群对克莱因四元群V4的商群，恰好是S3群，V4群可以看成是C2群的直积，可解，S3群可解，所以四次方程一定可解，其可解群列是：

所以四次方程扩域2*3*2*2=24次=4！，即可得到根域，deepseek得到的答案：

预解式的选取并不是唯一的，比如知道S4有一个D4子群，它是8阶的，我们可以根据D4去设计在8种置换下，其值保持不变的有理式，比如有理式：

在S4的24种置换下只有三个值，这样，方程

必然可以降阶为3次方程（y1,y2,y3是D4群的置换结果，牛顿定理保证了其可以转化为基本对陈多项式，从而可以用系数域表示），利用三次方程求根公式得到.

回过头来反思一下，为何伽罗瓦群公里第三条要求群运算是封闭的，大概就是因为只有满足封闭性的条件下，任何群作用的组合都是群内的元素，我们才能找到（穷尽）这样一系列关于根的有理式，无论在怎样的置换下，得到的值总是固定的，实现根式扩张。

ds的回答，保持多项式不变的群确实是D4群：

cayley图表示，克莱因四元群是D4群的一个正规子群，子群和陪集构成了一个十字交叉的形状。

实际上，S4群有三个D4子群，虽然它们不是正规的，但是可以利用D4构造根的有理式，从而得到以有理式为根的拉格朗日预解式，这三个D4群分别是：

显然D4群并非S4的正规子群，因为正规子群要求，若存在多个共轭子群，则单个子群不可能是正规的，就不可能出现上面三个D4子群了.

但是好像仍然能够用D4群进行中间扩域。四次方程的可解性由S₄的可解性保证（S₄的正规子群链为 ）和D4无关，但貌似尽管D4非正规，但预解式的存在允许直接构造根式解，无需依赖D4的正规性，这里还不太明白，貌似似乎是比伽罗瓦大定理更弱的一个条件。

解构A4

---

结束