2023年2月7日晚，我在图灵社区主办的“图灵八点半”栏目中分享了这个话题(视频请见“图灵社区”的微信视频号，见2月7日的直播回放)。现在我把文字稿进一步完善一下，分享到这里。
各位朋友，大家晚上好。我是来自浙江省永嘉中学的数学教师叶卢庆，同时也是人民邮电出版社最近出版的《微积分溯源：伟大思想的历程》的翻译者之一，负责第一章的翻译。很高兴能参加图灵社区组织的图灵八点半活动。在这里我想分享《微积分溯源》中的一个小故事，就是阿基米德是如何用力学方法发现球的体积公式的。
我们知道数学的历史发展顺序和数学教科书中呈现的逻辑顺序往往是不一致的，对于微积分来说尤其如此。现在的微积分教材往往是先讲极限、再讲微分，然后讲积分和级数。但是在历史上，积分是最先被研究的，而极限的严格定义直到19世纪才完成。在学习体系严密的教科书之余，了解微积分发展的真实历史会给我们很大的启发，它让我们了解到各种数学概念产生的自然背景，以及数学家在创造数学的过程中表现出来的真实的激情和困惑。
对积分的研究在古希腊其实就已经开始了，因为当时的数学家提出和解决了一些涉及面积和体积的问题，而这些问题的解决必定会在本质上涉及到积分。阿基米德是其中一个伟大的先驱者。阿基米德是公元前200多年以前(注：约公元前 287—公元前 212)的大数学家、力学家、工程师。他有很多故事流传下来，比如他发明了一些武器帮助西西里岛抵御罗马人的侵略，还比如他在被罗马士兵杀死之前还在研究数学。为了纪念他，现在的数学界最高奖项之一菲尔兹奖奖章的正面印着的就是阿基米德像。
图2.菲尔兹奖章正面的阿基米德像.图片来源：维基百科
大家来看这个菲尔兹奖章，上面有一列竖着写的希腊文，意思就是“阿基米德的像”，而奖章边缘绕着写的一行字是拉丁文，意思是“超越自我，掌握世界”。我想这就是数学的一个功能，他能帮助我们突破人类自身感官的局限性，用思维来理解世界的运行规律。
图3.菲尔兹奖章的背面.图片来源：维基百科
在菲尔兹奖章的背面有一行拉丁文，意思是“汇聚全世界数学家，表彰杰出工作”。而菲尔兹奖得主本人的名字，以及得奖年份是刻在奖章的侧边上，是很小的一行字。除此之外，奖章背面还有几束橄榄枝，橄榄枝后面被遮住了一部分图形，这就是我们今天要重点讨论的内容。被遮住的这个东西其实是一个圆柱，圆柱里面内切了一个球。
这个东西是什么呢？它是阿基米德的墓碑。阿基米德最先发现了球的体积公式，他把发现的结果表述为“球的体积是容纳球的最小圆柱体积的”.这是他一生最珍视的结果，所以他把这个结果刻在自己的墓碑上。当然现在这个墓碑已经找不到了，但是它刻在了数学界最高奖的奖章上。
图4.容纳球的最小圆柱
我们都在高中学过球的体积公式，知道球的体积 等于，其中 是球的半径。那么问题来了，阿基米德为什么不直接写出这个公式作为球的体积公式，而是看似“多此一举”地额外引进一个圆柱呢？这里我稍微解释一下，因为在古希腊的时候，数学约等于图形几何学,我们知道平面几何的逻辑体系就是古希腊数学家整理出来的，可以说它们对几何图形的研究已经炉火纯青，相比之下代数学就没发展得那么好。那时候的数学家习惯用图形之间的关系来表达公式、呈现推理.在18世纪早期人们才第一次用 π 来表示圆的周长与直径之比(欧拉推广了这个记号).阿基米德出生得太早了！
其实稍微想一下就可以知道阿基米德的结果和我们现在已知的球的体积公式是等价的：圆柱的地面半径为 ,高为 ,可得圆柱的体积是 .圆柱体积的是.
图5.
对于现在来说，阿基米德的结果已经是大一学生或者高三学生的一个简单的定积分习题：如图5所示,设经过球心的水平面高度为0 .在高度 处切一片圆盘薄片,截面半径设为 ,厚度是无穷小量 ,则圆盘薄片的体积忽略高阶无穷小量后可以视为 ,由勾股定理,圆盘薄片的体积是 .然后，将所有薄片的体积从高度 0 开始积分，一直积到高度r ,可得半球的体积等于定积分
拆开可得
由牛顿-莱布尼兹公式,或者说微积分基本定理,可得结果等于.所以球的体积是,干净利落地得到了结果. (注：以上推导过程合并起来叙述如下：
当然,这些结果都是基于后来数学的发展之上的,比如积分号是莱布尼兹引入的，而微积分基本定理是牛顿和莱布尼兹发现的.阿基米德本人不可能这样做.下面我们来介绍阿基米德的独特方法.
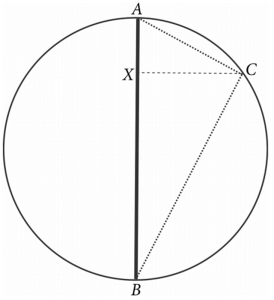
图6.
如图6,阿基米德将球面看作圆绕其直径 AB 旋转一周所得, 而且设想球体由垂直于直径 AB 的薄片堆积而成，下面这幅将苹果切成片的图是一个形象的展示.
图7.
当然，我们实际上切成的薄片要薄得多，以至于每个薄片的厚度是个无穷小量.就像图8里这样,我们可以用金黄的颜色标出其中一块薄片的边缘.
图8
这样看来,线段实际上是通过球心的.如图6,过上任意一点，选取一片垂直于的薄片， 是薄片边缘上的一点，则薄片的截面积可以看作 ，薄片厚度是无穷小量 .则将所有薄片体积求和，忽略高阶无穷小量，结果就是球的体积: 球的体积
球的体积
由勾股定理，,所以球的体积进一步表示成
而且我们发现三角形 和三角形相似,因此
即 ,把它代入球的体积表达式，可得
这样，问题就转化为如何求 和 .
然后阿基米德有一个重要观察：阿基米德发现， 是有几何意义的，它是某个圆锥的体积！
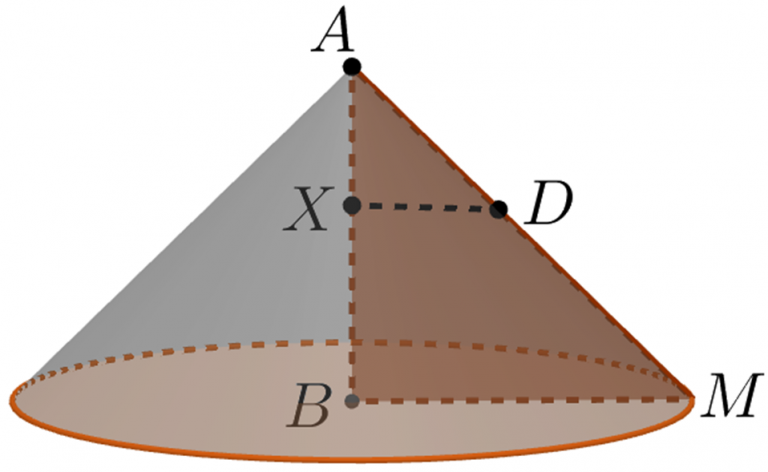
图9
这个圆锥可以这样构造：如图9所示,过直径上的任意一点 作直径 的垂线段，垂线段延申到点，使得 .当 在线段上到处移动，以至于遍历线段上的每一个点时，线段拖出一个阴影区域，是一个等腰直角三角形.然后将等腰直角三角形绕轴旋转一周，就得到了想要的圆锥.
事实上,对于构造出的这个圆锥来说，如果也把它分成无数片垂直于轴的圆盘薄片，那么经过点的薄片面积是 ,薄片的厚度是无穷小量 ,因此忽略高阶无穷小,可得薄片的体积是 .将所有薄片的体积求和,即可得圆锥的体积 .
而阿基米德和当时的数学家已经知道，圆锥体积是等底等高圆柱体积的.对于我们构造出的这个圆锥来说，与它对应的同底等高的圆柱的底面半径是容纳球的最小圆柱半径的2倍，高相等，因此与圆锥同底等高的圆柱的体积是容纳球的最小圆柱体积的4倍.所以，我们构造出的圆锥的体积是容纳球的最小圆柱体积的倍.这样我们就把等式(1)变成
现在阿基米德剩下最后一个任务，那就是求 .为此他借助了他自己发现的杠杆原理. 我们都知道阿基米德说过一句豪言壮语：“给我一个支点，我可以撬动地球！”这句话说的其实就是他发现的杠杆原理.
图10.
复习一下，杠杆原理说的是，给一个支点，支点上放一根重量不计的杠杆，杠杆两边放两个重物A,B.则杠杆保持平衡的条件是A 的质量乘以A 到支点的距离，等于 B的质量，乘以 B到支点的距离.
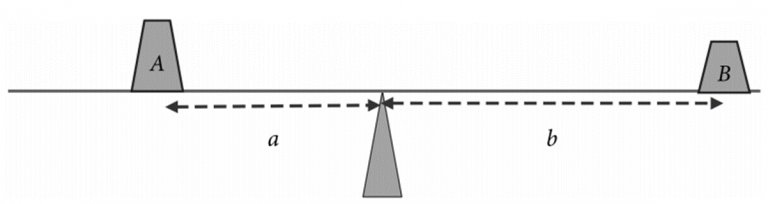
图11. 杠杆保持平衡
当 A 代表地球时，只要 B 到支点的距离 b足够大，那么杠杆就可以保持平衡，此时，阿基米德也就撬起了地球.当然这是一个玩笑. 言归正传,阿基米德为了求 ,先将公式(2)两边同时乘以长度 AB,得到
设涉及到的所有的材料密度是1 .那么我们就有下面的公式
这条公式是涉及到质量和长度的乘积的一个等式,仔细观察就可以联想到,这其实是一个体现力矩平衡的表达式! 这是阿基米德的天才发现.观察等式(3)右边的表达式 ,它是某个圆柱对支点产生的总力矩.让我们看图12,那个圆柱可以这样构造:让圆柱的一端放在支点,另一端与支点的距离恰好为 AB 的长度,而且让圆柱的地面半径也恰好是 AB的长度.则圆柱对支点产生的总力矩就是 .
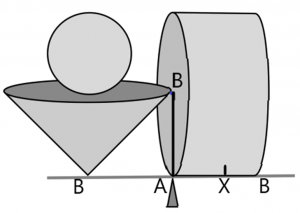
图12.
事实上,在圆柱的侧面边缘上取一点 X,经过 X 作一个薄片平行于圆柱底面,则薄片的面积为 ,薄片的厚度是无穷小量 ,于是薄片的体积是 .又因为材料的密度是1 ,所以薄片的质量也是 .且薄片与支点的距离是AX,所以薄片对支点产生的力矩是 .将所有薄片对支点产生的力矩求和,就得到圆柱对支点产生的力矩 .
换一个角度看,也可以这样计算圆柱对支点产生的力矩:把圆柱的所有质量集中在圆柱的中心,质量中心与支点的距离是.这个时候质量中心对支点产生的力矩,就是整个圆柱对支点的力矩.由于圆柱的底面半径是容纳球的最小圆柱的底面半径的2倍,高相等,所以圆柱的质量是容纳球的最小圆柱的质量的4倍.所以(3)式变为
当然,为了体现出力矩互相抵消的关系,我们在图12,支点的左边距离支点AB的地方放上了我们构造出来的圆锥和想要求出体积的球体,等式(3)和等式(4)成立意味着图12的杠杆保持平衡.
最后,消去等式(4)中的AB ,可以解得 球体的质量容纳球的最小圆柱的质量.由于质量之比等于体积之比,因此球体的体积容纳球的最小圆柱的体积.这样阿基米德就利用他精湛的力学技巧,得到了他著名的球的体积公式.
这一切都被阿基米德记载在他的著作 力学定理的方法中.这是阿基米德差点失传的著作,直到1906年才被人从一本羊皮书中发现,书中阿基米德的文字已经被人擦掉,用其它文字覆盖了.后来人们用各种高科技,比如X光线照射,重新显现出了阿基米德的文字.
图13.《力学定理的方法》.
正如微积分溯源 的作者 Bressoud 指出的,
《力学定理的方法》是阿基米德写给同时代的数学家埃拉托斯特尼的书, 里面阐述了计算面积、体积和力矩的方法.书中展示了积分学的核心思想, 包括对无穷小量的运用, 只不过阿基米德在书写形式证明的时候隐藏了这些想法.
只要数学继续存在,阿基米德在求解数学问题中体现出来的创造力将永远流传下去,阿基米德是永恒的数学家.我的分享就到这里.谢谢大家.
推荐阅读
作者：[美]戴维·M. 布雷苏（David M. Bressoud）
译者：陈见柯 林开亮 叶卢庆
美国数学协会推荐读物，汤涛院士推荐
一堂“新角度”微积分数学课，带你回溯微积分的起源与思想发展历程
前美国数学协会会长、《高等微积分》作者戴维•M.布雷苏最新数学科普作品
3
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
