概率论教材这么多，这本凭什么能畅销6万册！

turingbooks

于 2023-11-09 11:20:49 发布

阅读量907

点赞数

文章标签：概率论

原文链接：https://mp.weixin.qq.com/s?__biz=MjM5Njc0MjIwMA==&mid=2649805267&idx=1&sn=94ac662a8033d4a952df762b7def16ed&chksm=bee0e48489976d92078df29da43509f5ca320e0763ef630d101da961b970712d2eb543c567e2&scene=126&sessionid=0

版权

本文介绍了概率论，它是研究随机现象数量规律的学科，与实际联系紧密。文中讲述了其发展简史、公理化体系建立，介绍了现代概率论的研究内容，如极限理论、马尔可夫过程等，还阐述了其在物理、生物、通信等领域的应用，最后推荐了多本概率论相关书籍。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

针对概率论，有法国牛顿之称的拉普拉斯（1749年-1827年）曾说：“这门源自赌博机运之科学，必将成为人类知识中最重要的一部分，生活中大多数问题，都将只是概率的问题。”

目前，概率论也和微积分、线性代数一同成为数学三大基础学科，同时也是考研的基本内容。但这一门课却并不好学，尽管概率论的基本直观概念早已渗透到人们的工作和生活当中，小到人人都可以买到的彩票，大到星辰宇宙，复杂到计算机和人工智能，都与概率密切相关。

图灵出版的这本《普林斯顿概率论读本》堪称最好的入门书，从基础入门开始淳淳教导，有证明，有深度，有趣味，通俗易懂，书中配有丰富的例子和大量习题，对于学习具有很好的启发性。3年累计销售6万多册，豆瓣更是打出9.3的高分！可见大家对这本书的高度认可了！

来源 | 本文转自科学网

作者 | 王寿仁

概率论，研究随机现象数量规律的数学分支学科。随机现象是指这样的客观现象，当人们观察它时，所得的结果不能预先确定，而只是多种可能结果中的一种。

在自然界和人类社会中，存在着大量的随机现象。例如，掷一硬币，可能出现正面或反面；测量一物体长度，由于仪器及观察受到环境的影响，每次测量结果可能有差异；在同一工艺条件下生产出的灯泡，其寿命长短参差不齐，等等。典型的随机实验有掷骰子、扔硬币、抽扑克牌以及轮盘游戏等。

数学家和精算师认为概率是在0至1之间之闭区间的数字，指定给一发生与失败是随机的“事件”。概率P(A)根据概率公理来指定给事件A。

一事件A在一事件B确定发生后会发生的概率称为B给之A的条件概率；其数值为(当P(A)不等于零时)。若B给之A的条件概率和A的概率相同时，则称A和B为独立事件。且A和B的此一关系为对称的，这可以由一同价叙述：“，当A和B为独立事件时。”中看出。

概率论中的两个重要概念为随机变量和随机变量之概率分布这两种概念。

在实际中，人们往往还需要研究在时间推进中某一特定随机现象的演变情况，描述这种演变的就是概率论中的随机过程。

例如，某一电话交换台从一确定时刻起到其后的每一时刻为止所收到的呼唤次数便是一随机过程。又如，微小粒子在液体中因受周围分子的随机碰撞而形成不规则的运动（即布朗运动）也是一随机过程。

研究随机过程的统计特性，计算与过程有关的某些事件的概率，特别是研究与过程样本轨道（即过程的一次实现）有关的问题，是现代概率论的主要课题。总之，概率论与实际有着密切的联系，它在自然科学、技术科学、社会科学、军事和工农业生产中都有广泛的应用。概率论还是数理统计学的理论基础。

概率论发展简史

概率论有悠久的历史，它的起源与博弈问题有关。16世纪，意大利的一些学者开始研究掷骰子等赌博中的一些简单问题，例如比较掷两个骰子出现总点数为9或10的可能性大小。

17世纪中叶，法国数学家B.帕斯卡、P.de费马及荷兰数学家C.惠更斯基于排列组合的方法研究了一些较复杂的赌博问题，他们解决了“合理分配赌注问题”（即“得分问题”）、“输光问题”等等。其方法不是直接计算赌徒赢局的概率，而是计算期望的赢值，从而导致了现今称之为数学期望的概念（由惠更斯明确提出）。

使概率论成为数学的一个分支的真正奠基人则是瑞士数学家雅各布·伯努利，他建立了概率论中第一个极限定理，即伯努利大数律；该定理断言:设事件的概率，其中。若表示前次独立重复试验中事件出现的次数，从而为事件出现的频率，则当时，


雅各布·伯努利 (Jakob Bernoulli‎, 1654-1705)	高斯 (C. F. Gauss, 1777-1855)

式中为任一正实数。这一结果发表于他死后8年(1713)出版的遗著《推测术》(Ars conjectandi)中。这里所说的事件的概率，应理解为事件发生的机会的一个测度，即公理化概率测度。

1716年前后，A.棣莫弗对p=1/2情形，用他导出的关于n!的渐近公式(，即所谓斯特林公式)进一步证明了渐近地服从正态分布（德国数学家C.F.高斯于1809年研究测量误差理论时重新导出正态分布，所以也称为高斯分布）。

棣莫弗的这一结果后来被法国数学家P.-S.拉普拉斯拉普拉斯推广到一般的的情形，后世称之为棣莫弗-拉普拉斯极限定理，这是概率论中第二个基本极限定理的原始形式。

拉普拉斯对概率论的发展贡献很大。他在系统总结前人工作的基础上，写出了《概率的分析理论》(1812年出版，后又再版6次)。在这一著作中，他首次明确规定了概率的古典定义（通常称为古典概率），并在概率论中引入了更有力的分析工具，如差分方程、母函数等，从而实现了概率论由单纯的组合计算到分析方法的过渡，将概率论推向一个新的发展阶段。拉普拉斯非常重视概率论的实际应用，对人口统计学尤其感兴趣。


棣莫弗 (Abraham De Moivre, 1667-1754)	拉普拉斯 (Pierre-Simon Laplace, 1749-1827)

继拉普拉斯以后，概率论的中心研究课题是推广和改进伯努利大数律及棣莫弗－拉普拉斯极限定理。在这方面，俄国数学家 П.Л.切比雪夫迈出了决定性的一步，1866年他用他所创立的切比雪夫不等式建立了有关独立随机变量序列的大数律。次年，又建立了有关各阶绝对矩一致有界的独立随机变量序列的中心极限定理；但其证明不严格，后来由Α.Α.马尔可夫于1898年补证。

1901年Α.М.李亚普诺夫利用特征函数方法，对一类相当广泛的独立随机变量序列，证明了中心极限定理。他还利用这一定理第一次科学地解释了为什么实际中遇到的许多随机变量近似服从正态分布。

继李亚普诺夫之后，Α.Я.辛钦、Α.Η.柯尔莫哥洛夫、P.莱维及W.费勒等人在随机变量序列的极限理论方面作出了重要贡献。到20世纪30年代，有关独立随机变量序列的极限理论已臻完备。在此期间，由于实际问题的需要，特别是受物理学的刺激，人们开始研究随机过程。


马尔可夫（A.A.Markov, 1856－1922）	柯尔莫哥洛夫 (Andrey N. Kolmogorov, 1903－1987）

1905年A.爱因斯坦和R.斯莫卢霍夫斯基各自独立地研究了布朗运动。他们用不同的概率模型求得了运动质点的转移密度。

但直到1923年，N.维纳才利用三角级数首次给出了布朗运动的严格数学定义，并证明了布朗运动轨道的连续性。

1907年马尔可夫在研究相依随机变量序列时，提出了现今称之为马尔可夫链的概念；而马尔可夫过程的理论基础则由柯尔莫哥洛夫在1931年所奠定。稍后一些时候，辛钦研究了平稳过程的相关理论(1934)。

所有这些关于随机过程的研究，都是基于分析方法，即将概率问题化为微分方程或泛函分析等问题来解决。从1938年开始，莱维系统深入地研究了布朗运动，取得了一系列重要成果，他充分利用概率的直觉性，将逻辑与直觉结合起来，倡导了研究随机过程的一种新方法，即概率方法。这种方法的特点是着眼于随机过程的轨道性质。

莱维对概率论的另一重要贡献是建立了独立增量过程的一般理论。他的著作《随机过程与布朗运动》(1948)至今仍是随机过程理论的一本经典著作。现代概率论的另外两个代表人物是J.L.杜布和伊藤清，前者创立了鞅论，后者创立了布朗运动的随机积分理论。

在概率发展史中特别值得一提的是柯尔莫哥洛夫在1933年建立了概率论的公理化体系。

概率论公理化体系的建立

早在拉普拉斯给出概率的古典定义之前，人们就提出了几何概率的概念，这是研究有无穷多个可能结果的随机现象问题的，著名的布丰（曾译蒲丰）投针问题(1777)就是几何概率的一个早期例子。19世纪，几何概率逐步发展起来。但到19世纪末，出现了一些自相矛盾的结果。几何概率这类问题说明了拉普拉斯关于概率的古典定义带有很大的局限性。当严密的概率公理化系统建立后，几何概率才能健康地发展且有广泛的应用。

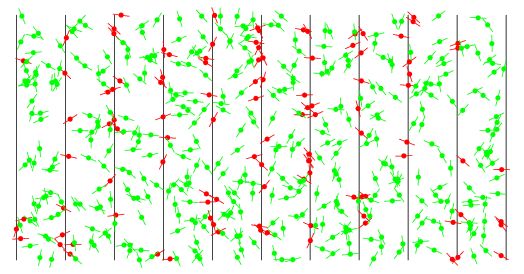
布丰投针问题投掷：500颗针后的分布

虽然到了19世纪下半叶，概率论在统计物理学中的应用及概率论的自身发展已突破了概率的古典定义，但关于概率的一般定义则始终未能明确化和严格化。这种情况既严重阻碍了概率论的进一步发展和应用，又落后于当时数学的其他分支的公理化潮流。

1900年，D.希尔伯特在世界数学家大会上公开提出了建立概率论公理化体系的问题，最先从事这方面研究的是庞加莱、波莱尔及С.Η.伯恩斯坦。关于概率论与测度论有联系这一重要思想就出自波莱尔。伯恩斯坦于1917年构造了概率论的第一个公理化体系。

20年代以后，相继出现了J.M.凯恩斯及R.von米泽斯等人的工作。凯恩斯主张把任何命题都看作是事件。例如，“明天将下雨”，“土星上有生命”，“某出土文物是某年代的产品”，等等。他把一事件的概率看作是人们根据经验对该事件的可信程度，而与随机试验没有直接联系，因此，通常称为主观概率。

从凯恩斯起，对主观概率提出了几种公理体系，但没有一种堪称权威。也许，主观概率的最大影响不在概率论领域自身，而在数理统计学中近年来出现的贝叶斯统计学派。

和主观概率学派相对立的是以米泽斯为代表的概率的频率理论学派。米泽斯把一事件的概率定义为该事件在独立重复随机试验中出现的频率的极限，并把此极限的存在性作为他的第一条公理。他的第二条公理是，对随机选取的子试验序列，事件出现的频率的极限也存在并且极限值相等。


布丰（Georges Louis Leclere de Buffo, 1707—1788）	波莱尔（Emile Borel, 1871-1956）

严格说来，这第二条公理没有确切的数学含义。因此，这种所谓公理化在数学上是不可取的。此外，象某个事件在一独立重复试验序列中出现无穷多次这一事件的概率，在米泽斯理论中是无法定义的。这种频率法的理论依据是强大数律，它具有较强的直观性，易为实际工作者和物理学家所接受。但随着科学的进步，它又已逐渐被绝大多数物理学家所抛弃。

20世纪初完成的勒贝格测度和勒贝格积分理论以及随后发展起来的抽象测度和积分理论，为概率论公理体系的确立奠定了理论基础。人们通过对概率论的两个最基本的概念即事件与概率的长期研究，发现事件的运算与集合的运算完全类似，概率与测度有相同的性质。

到了30年代，随着大数律研究的深入，概率论与测度论的联系愈来愈明显。例如强、弱大数律中的收敛性与测度论中的几乎处处收敛及依测度收敛完全类似。在这种背景下，柯尔莫哥洛夫于1933年在他的《概率论基础》一书中第一次给出了概率的测度论式的定义和一套严密的公理体系。这一公理体系着眼于规定事件及事件概率的最基本的性质和关系，并用这些规定来表明概率的运算法则。

它们是从客观实际中抽象出来的，既概括了概率的古典定义、几何定义及频率定义的基本特性，又避免了各自的局限性和含混之处。这一公理体系一经提出，便迅速获得举世的公认。它的出现，是概率论发展史上的一个里程碑，为现代概率论的蓬勃发展打下了坚实的基础。

现代概率论的内容

由于科学技术中许多实际问题的推动以及概率论逻辑基础的建立，概率论从20世纪30年代以来得到了迅速的发展。

目前其主要研究内容大致可分为极限理论，独立增量过程，马尔可夫过程，平稳过程和时间序列，鞅和随机微分方程，点过程等。此外，包括组合概率（用组合数学方法解决只涉及有限个基本事件的概率问题）、几何概率等在内的一些属于古典范畴的问题，至今仍有人在继续研究，并有新的发展。

极限理论是研究与随机变量序列或随机过程序列的收敛性有关的问题的理论。20世纪30年代以后，有关随机变量序列的极限理论（主要是中心极限定理）的研究，是将独立序列情形的结果推广到鞅差序列和更一般的弱相依序列等情形，以及研究收敛速度问题。近年来，由于统计力学的需要，人们开始研究强相依随机变量序列的非中心极限定理。

自1951年M.唐斯克提出不变原理后，有关随机过程序列的弱收敛的研究成了极限理论的一个中心课题。ю.Β.普罗霍洛夫及A.B.斯科罗霍德在这方面作出了最主要的贡献。1964年V.斯特拉森的工作出现后，引起了有关随机过程序列的强收敛的研究，这就是强不变原理。近年来，鞅论方法已渗透到这一领域，使许多经典结果的证明得到简化和统一处理，并且还导致一些新的结果。

人们最早知道的独立增量过程是在物理现象中观察到的布朗运动和泊松过程，一般的独立增量过程的研究，归功于莱维，它在20世纪40年代已臻成熟。在这些研究中，包含了许多重要的方法和概念，概率论的许多近代研究课题都直接或间接地受其启发与影响。

在实际中遇到的很多随机现象有如下的共同特性：它的未来的演变，在已知它目前状态的条件下与以往的状况无关。描述这种随时间推进的随机现象的演变模型就是马尔可夫过程。

20世纪50年代以前，研究马尔可夫过程的主要工具是微分方程和半群理论（即分析方法）；1936年前后就开始探讨马尔可夫过程的轨道性质，直到把微分方程和半群理论的分析方法同研究轨道性质的概率方法结合运用，才使这方面的研究工作进一步深化，并形成了对轨道分析必不可少的强马尔可夫性概念。

1942年，伊藤清用他创立的随机积分和随机微分方程理论来研究一类特殊而重要的马尔可夫过程──扩散过程，开辟了研究马尔可夫过程的又一重要途径。近年来，鞅论方法也已渗透到马尔可夫过程的研究中，它与随机微分方程结合在一起，已成为目前处理多维扩散过程的工具。

此外，马尔可夫过程与分析学中的位势论有密切的联系。对马尔可夫过程的研究，推动了位势理论的发展，并为研究偏微分方程提供了概率论的方法。最近十多年发展起来的吉布斯随机场和无穷粒子随机系统，是由于统计物理的需要而提出的。

许多自然的和生产过程中的随机现象表现出某种平稳性。一种平稳性是过程在任意一些时刻上的联合概率分布随时间推移不变，这种平稳性称为严平稳性。平稳过程的研究与遍历理论有密切的联系。如果上述对概率分布的要求放宽为仅对二阶相关矩的要求，即过程在任意两时刻上的协方差随时间推移不变，则称这种平稳性为宽平稳性。

关于宽平稳过程的研究，辛钦、柯尔莫哥洛夫和维纳等人运用傅里叶分析和泛函分析的工具，在40年代已经找出了过程的相关函数及过程本身的谱分解式，并且较完满地解决了有应用意义的预测问题。许多应用问题还要求根据观测数据去建立这些数据所来自的随机过程的模型。为此产生了时间序列分析这一课题，提出了宽平稳序列的自回归滑动平均(ARMA)模型以及一些非线性模型。

鞅是另一类重要的随机过程。从20世纪30年代起，莱维等人就开始研究鞅序列，把它作为独立随机变量序列的部分和的推广。40年代到50年代初，杜布对鞅进行了系统的研究，得到有名的鞅不等式、停止定理和收敛定理等重要结果。

1962年，P.A.迈耶解决了杜布提出的连续时间的上鞅分解为鞅及增过程之差的问题。在解决这个问题的过程中，出现了很多新鲜而深刻的概念，使鞅和随机过程一般理论的内容大大丰富起来。鞅的研究丰富了概率论的内容，并引起人们用它所提供的新方法新概念对概率论中许多经典的内容重新审议，把以往认为是复杂的东西纳入鞅论的框架而加以简化。

此外，利用上鞅的分解定理，可以把伊藤清的对布朗运动的随机积分推广到对一般鞅乃至半鞅的随机积分；因而，更一般的随机微分方程的研究也随之发展。随机微分方程理论不仅可以用来研究马尔可夫过程，它还是解决滤波问题的必要工具。最近出现的流形上的随机微分方程又和微分几何及分析力学的研究发生了密切的联系。鞅论还对本学科以外的位势理论、调和分析及复变函数论等提供了有用的工具。

点过程是从所谓计数过程发展出来的，它们的特点是，可用落在不相重叠的集合上的随机点数目的联合概率分布来刻画整个过程的概率规律。最基本的计数过程是泊松过程，1943年，C.帕尔姆将它作为最简单的输入流应用于研究电话业务问题；1955年，辛钦又以严密的数学观点作了整理和发展。

在60年代以前，点过程的研究主要限于泊松过程及其推广的过程。以后，由于大量实际问题的需要以及随机测度论和现代鞅论的推动，进一步把实轴上的点过程（即计数过程）推广到一般的可分完备度量空间上，在内容和方法上都有根本性的进展。

现代概率论的应用

随机引起的流体力学的湍流

概率论的发展史说明了理论与实际之间的密切关系。许多研究方向的提出，归根到底是有其实际背景的。反过来，当这些方向被深入研究后，又可指导实践，进一步扩大和深化应用范围。概率论作为数理统计学的理论基础是尽人皆知的。下面简略介绍一下概率论本身在各方面的应用情况。

在物理学方面，高能电子或核子穿过吸收体时，产生级联（或倍增）现象,在研究电了-光子级联过程的起伏问题时，要用到随机过程，常以泊松过程、弗瑞过程或波伊亚过程作为实际级联的近似，有时还要用到更新过程（见点过程）的概念。当核子穿到吸收体的某一深度时，则可用扩散方程来计算核子的概率分布。物理学中的放射性衰变，粒子计数器，原子核照相乳胶中的径迹理论和原子核反应堆中的问题等的研究，都要用到泊松过程和更新理论。湍流理论以及天文学中的星云密度起伏、辐射传递等研究要用到随机场的理论。探讨太阳黑子的规律及其预测时，时间序列方法非常有用。

化学反应动力学中，研究化学反应的时变率及影响这些时变率的因素问题,自动催化反应，单分子反应,双分子反应及一些连锁反应的动力学模型等，都要以生灭过程（见马尔可夫过程）来描述。

随机过程理论所提供的方法对于生物数学具有很大的重要性，许多研究工作者以此来构造生物现象的模型。研究群体的增长问题时，提出了生灭型随机模型，两性增长模型，群体间竞争与生尅模型，群体迁移模型，增长过程的扩散模型等等。有些生物现象还可以利用时间序列模型来进行预报。传染病流行问题要用到具有有限个状态的多变量非线性生灭过程。在遗传问题中，着重研究群体经过多少代遗传后，进入某一固定类和首次进入此固定类的时间，以及最大基因频率的分布等。

随机性在生物系统里起着重要的作用

许多服务系统，如电话通信，船舶装卸，机器损修，病人候诊，红绿灯交换，存货控制，水库调度，购货排队，等等，都可用一类概率模型来描述。这类概率模型涉及的过程叫排队过程，它是点过程的特例。排队过程一般不是马尔可夫型的。当把顾客到达和服务所需时间的统计规律研究清楚后，就可以合理安排服务点。

在通信、雷达探测、地震探测等领域中，都有传递信号与接收信号的问题。传递信号时会受到噪声的干扰，为了准确地传递和接收信号，就要把干扰的性质分析清楚，然后采取办法消除干扰。这是信息论的主要目的。噪声本身是随机的，所以概率论是信息论研究中必不可少的工具。信息论中的滤波问题就是研究在接收信号时如何最大限度地消除噪声的干扰，而编码问题则是研究采取什么样的手段发射信号，能最大限度地抵抗干扰。在空间科学和工业生产的自动化技术中需要用到信息论和控制理论，而研究带随机干扰的控制问题，也要用到概率论方法。

概率论进入其他科学领域的趋势还在不断发展。值得指出的是，在纯数学领域内用概率论方法研究数论问题已经有很好的结果。在社会科学领域，特别是经济学中研究最优决策和经济的稳定增长等问题，也大量采用概率论方法。正如拉普拉斯所说：“生活中最重要的问题，其中绝大多数在实质上只是概率的问题。”

《普林斯顿概率论读本》

作者：[美] 史蒂文·J. 米勒（Steven J. Miller）

译者：李馨

普林斯顿读本三剑客之概率论，概率论教材，叙述深入浅出，提供课程视频和讲义，概率论学习图书。

对于学生来说，学习概率论及其众多应用、技术和方法似乎非常费力且令人生畏，而这正是本书的用武之地。这本通俗易懂的学习指南旨在用作概率论的独立教材或相关课程的补充材料，可帮助学生轻松地学习概率论知识并取得良好效果。

本书基于史蒂文·J. 米勒在布朗大学、曼荷莲学院和威廉姆斯学院教授的课程而作。米勒通过先修课程材料、各种难度的问题及证明对概率论这一数学领域进行了详细介绍。探索每个主题时，米勒首先引导学生运用直觉，然后才深入技术细节。本书涵盖的主题很广，并且对材料加以重复以强化知识。读完本书，学生不仅能掌握概率论，还能为将来学习其他课程打下基础。