豆瓣9.6，全球影响广泛，这本数学著作为什么不可替代？

在一门有近 200 年历史, 而且已经有了数十部公认名著的基础分支学科里, 能够写出如此不同凡响的著作, 实在难得。

—— 著名数学家  齐民友

这本深受好评的数学著作就是《复分析：可视化方法》，它的出版当年在数学界曾经引起过不小震动，为什么这本书在数学圈不可替代？

作者尼达姆独辟蹊径，用一种真正不同寻常的、独具创造性的视角和可以看得见的论证方式解释初等复分析的理论，用丰富的图例展示各种概念、定理和证明思路，十分便于读者理解，充分揭示了复分析的数学美。

《复分析：可视化方法》

作者：[美] 特里斯坦·尼达姆

译者：齐民友

01

沉睡的复数，爆炸式发展的复分析

从最初发现复数以来,已经过了 4 个半世纪.现在,读者可能已经知道,复数这个词讲的是一个形如 a + ib 的整体, 这里 a, b 是通常的实数,而 i 和任何普通的数都不同,具有 i² = −1 这个性质.

这个发现最终对整个数学有深远的影响,把许多原来根本不同的东西统一起来,解释了许多原来似乎不能理解的事情.

尽管有这样的好结局——事实上故事还在继续——但是从复数最初发现以来, 进展慢得令人痛苦. 说真的, 与 19 世纪以后所取得的进展比较, 复数生存的前250年里, 可以说几乎没有进展.

在那些如笛卡儿、费马、莱布尼茨那样伟大的智者甚至还有牛顿这样神话般的天才出生而又逝去的年代里, 复数怎么可能都完全沉睡着？答案似乎在于这样一个事实：复数一开始得到的并不是拥抱, 而是怀疑、困惑, 甚至是敌意.

1545 年出版的卡丹诺的《大术》（Ars Magna）一书, 通常被认为是复数的出生证. 然而, 即使在卡丹诺的著作中, 这种数也是一被引入就被他当作 “既不可捉摸又没有用处” 而加以摒弃. 

我们将会看到, 庞贝利在他 1572 年出版的《代数》（L’Algebra）一书中才第一次对复数进行了实际的计算. 甚至这时, 创新者似乎还否认（至少一开始是这样）复数是自己的创新, 说 “所有这些似乎是以诡辩而不是以真理为基础的”. 

晚到 1702 年, 莱布尼茨还把 −1 的平方根描述为 “介乎存在与不存在之间的两栖类”. 这种情绪似乎也在这个时期使用的名词上反映出来. 哪怕是讨论了复数, 复数仍被称为 “不可能数” 或 “虚数” （imaginary）.

很不幸, 后一个词直到今天仍然残留着.甚至到 1770 年时情况还很混乱, 甚至像欧拉这样伟大的数学家还错误地去论证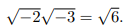

麻烦的根源似乎来自心理上或哲学上. 如果谁也不知道怎样回答 “什么是复数” 这个问题, 怎么可能热情而有信心地去研究这些事情呢？

直到 18 世纪末, 这个问题才有了令人满意的答案. 

 韦塞尔、阿尔冈和高斯,相继独立然而很快一个接一个地认识到, 可以给复数一个简单的具体的几何解释,即平面上的点（或向量）：应该把 a + ib 这个神秘的东西看成 xy 平面上以 (a, b) 为坐标的点, 或等价地看成连接原点到此点的向量. 见图 1-1. 这样来看待的平面记作 并称为复平面. 

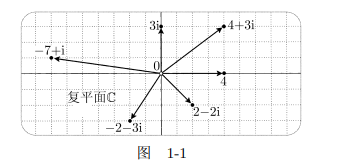
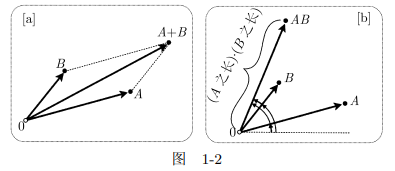
对两个复数的加法和乘法现在也可以赋予确定的几何意义, 即解释为平面上相应的点（或向量）的几何运算. 图 1-2a 演示了加法的法则：

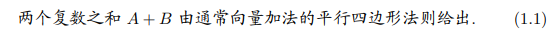
注意, 这与图 1-1 是相容的, 因为（举例来说）4 + 3i 确实是 4 与 3i 之和.图 1-2b 画出了不那么明显的乘法法则： 

这个法则并不是由图 1-1 就可以看出的. 但是要注意它至少与图 1-1 不矛盾, （举例来说）3i 确实是 3 与 i 的乘积, 请读者自己验证. i 与自身的乘积是一个更加令人兴奋的例子. 因为 i 有单位长, 而辐角为 (π/2), i² 也就有单位长与辐角 π. 所以i² = −1. 

韦塞尔和阿尔冈虽然发表了这个几何解释, 却未引起注意, 但是高斯的名声（当时已和今天一样显赫）保证了 “复数作为平面上的点” 得到广泛传播而普遍为人接受. 比起这个新解释看来不那么重要（至少一开始显得如此）的是这样一个事实：

现在终于有了某种办法使这种数有意义了―――它们现在终于成了合法的研究对象了. 不管怎么说, 伟大发现的闸门即将开启.

就复数达成共识花了 2 个半世纪还多, 但是怎样用这些数做微积分的美丽的新理论（即现在所谓复分析）却发展得快得令人吃惊. 绝大多数基本结果（由柯西、黎曼等人得出）是在 1814∼1851 年得到的―――期间还不到 40 年！ 

对这门学科的历史肯定可能有别的看法. 例如 Stewart and Tall指出, 比之复分析的爆炸式发展, 其几何解释就不那么重要了. 但是有一点必须提到, 如果事先不具备复平面的几何知识, 黎曼的思想是完全不可能的.

02

庞贝利的“奇想”

复分析的力量和美丽最终来自乘法法则 (1.2) 和加法法则 (1.1). 这些法则最初是由庞贝利以符号规则的形式给出的, 到两个多世纪以后才出现图 1-2. 因为原来似乎只是凭空抓出来了这些法则, 所以我们再回到 16 世纪以便理解其代数根源. 

许多教科书都按一种方便的历史虚构来引入复数, 即以求解二次方程

为基础. 大约在公元前 2000 年, 就已经知道这种方程的一种解法, 它等价于现代的公式

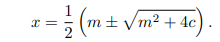
但是如果 m² + 4c 为负会如何？正是这个问题使得卡丹诺考虑负数的平方根.

到这一步为止, 这些教科书在历史方面都是正确的, 但是再往下就会读到这样的话：因为需要方程 (1.3) 有解, 就迫使我们严肃地考虑复数.

但是这种论据在今天也和在16 世纪一样, 几乎没有什么分量. 事实上, 我们已经指出, 卡丹诺毫不迟疑地摒弃这种解, 说它是 “没有用处” 的.

并不是卡丹诺缺少继续追究这件事所需的想象力, 而是他很有理由不去这样做. 

对于古希腊人, 数学就是几何学的同义语, 所以, 如 (1.3) 那样的代数关系式并不是作为代数问题来看待的, (1.3) 只是解决一个真正的几何问题的载体. 

例如,(1.3) 可以看成求抛物线 y = x² 与直线 y = mx + c 的交点. 见图 1-3a.

在 L₁ 的情况下, 问题确实有解; 从代数上说, (m² + 4c) > 0, 而两个交点则由上式给出. 在 L₂ 的情况下, 这个问题显然没有解; 从代数上说, (m2 + 4c) < 0, 公式中出现了 “不可能” 的数正确地宣示了解的不存在.

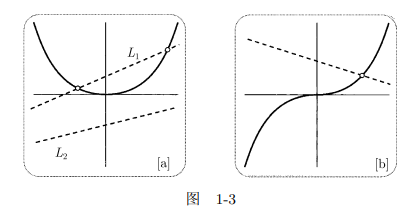
并不是二次方程迫使我们严肃地考虑复数, 而是三次方程

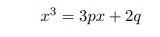
迫使人们这样做. [习题 1 表明, 一般的三次方程都可以化为这种形式.] 这个方程代表求一条三次曲线 y = x³ 与直线 y = 3px + 2q 的交点. 见图 1-3b. 卡丹诺的《大术》一书以菲洛 ①和塔塔里亚 ②的工作为基础, 证明了这个方程有以下的著名解式[见习题 2]：

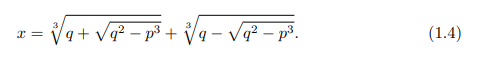
请读者用 x³ = 6x + 6 去试一试. 

这个公式出现大约 30 年后, 庞贝利看出来它有一些奇怪的悖论式的地方. 首先注意, 若直线 y = 3px + 2q 满足 p³ > q², 则公式中出现复数. 例如庞贝利考虑了x³ = 15x + 4, 得出

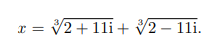
在图 1-3a 中, 出现复数表示几何问题无解, 但在图 1-3b 中, 这条直线一定会与曲线相交！事实上, 检验一下庞贝利的例子就会给出 x = 4.庞贝利在与这个悖论斗争中, 忽发 “奇想”：如果在上式中设

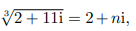
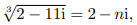
说不定就会给出 x = 4. 

当然, 为了使此法可行, 他必须假设两个复数 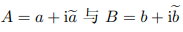的加法需服从一个似乎近情理的法则：

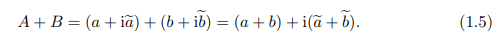
其次, 如果真正有一个值 n 能使 √32 + 11i = 2 + ni, 他就必须去计算 (2 + in)3. 为此, 他假设可以像通常代数中那样把括号乘开, 于是

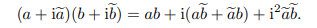
这个法则判明了他的 “奇想” 胜利, 因为现在他能够证明 (2 + i)³ = 2 + 11i, 请自行验证.

 尽管复数本身仍然是神秘的, 然而庞贝利关于三次方程的工作证实了, 完全实际的问题也需要用复算术来求解. 复数理论以后的发展也和它的诞生一样, 是与数学其他领域（还有物理学）的进展密不可分的. 

  推荐阅读

《复分析：可视化方法》

作者：[美]特里斯坦·尼达姆

译者：齐民友

本书用一种真正不同寻常的、独具创造性的视角和可以看得见的论证方式解释初等复分析的理论，公开挑战当前占统治地位的纯符号逻辑推理。

本书是在复分析领域产生了广泛影响的一本著作。作者独辟蹊径，用丰富的图例展示各种概念、定理和证明思路，十分便于读者理解，充分揭示了复分析的数学美。

《可视化微分几何和形式：一部五幕数学正剧》 

作者：[美]特里斯坦·尼达姆（Tristan Needham）

译者：刘伟安

1.旧金山大学数学系教授，理学院副院长，牛津大学博士，与霍金齐名的诺奖得主罗杰·彭罗斯弟子特里斯坦·尼达姆经典巨作！

2.200多幅手绘示意图，将“微分几何”回归为“几何”，运用牛顿的几何方法对经典结果做出了几何解释。

3.原著豆瓣高达9.9分！被认为是“小说一般流畅的数学教材！”

4.译者为国内著名偏微分方程专家，武汉大学原校长齐民友老师弟子、武汉大学数学教授刘伟安老师。