概率论为什么这么难学，这篇关于它的终极应用的文章终于讲清楚了！

turingbooks

于 2024-09-13 11:31:02 发布

阅读量559

点赞数

文章标签：概率论

原文链接：https://mp.weixin.qq.com/s?__biz=MjM5Njc0MjIwMA==&mid=2649821385&idx=2&sn=5b70106e5988d25c17c7f65f67a3b655&chksm=bf900b29b34c557690713070810d87a6bdc96b19828b6fd58e642d6dab7d7d7adc995626429f&scene=126&sessionid=0

版权

现代物理学研究已经证实，要精确预测每一次实验结果是不可能的，哪怕仅在大体上进行预测，也是不可能的。理论只能预测不同结果的可能性。很清楚，社会科学中的情况会变得更加复杂，因为社会科学中的各种相关因素往往交织在一起，而它们通常是很难确定的。

17 世纪的研究者们很快就发现，要寻找像牛顿的万有引力定律那样精确、普适的社会规律，从一开始就注定是不可能成功的。

就当前来说，把人类天性的复杂性引入方程式，要以此想获得确切的预测，这几乎是不可能的。如果把整个人类的心智都纳入考察范围内，那么就更没有希望了。然而，科学家们并没有气馁，一小批具有天才智慧的思想者们发展出了全新的、革命性的数学工具——统计学和概率论。

图书 | 《最后的数学问题》

作者：[美]马里奥•利维奥（Mario Livio）

译者：黄征

文摘 | 统计学家和概率学家：不确定的科学

碰运气的游戏

人们热心研究概率的起因颇有些不足挂齿：赌徒们试图调整自己的赌注，来增加赢的概率。特别是在17世纪中期，一位化名“梅雷骑士”（Chevalier de Méré）的法国贵族——他也是一位有名的赌徒——向当时法国著名的数学家和哲学家布莱兹·帕斯卡（Blaise Pascal，1623—1662）提出了一系列关于赌博的问题。帕斯卡在 1654 年与当时另一位著名的法国数学家皮埃尔·德·费马（Pierre de Fermat，1601—1665）之间频繁通信，在这些信中，他们就类似问题进行了深入的交流。事实上，概率论的基本理论就这样建立起来了。

让我们看看帕斯卡在 1654 年 7 月 29 日写给费马的一封信中讨论的一个有趣的问题。这个问题假设了有两位贵族，他们在玩一种赌博游戏，游戏的工具是一只骰子。在游戏开始之前，每个人都在桌子上放下了 32 枚金币作为赌资。

第一个人选择的是数字 1，而另一个人选择的是数字 5。如果掷出的骰子向上的一面出现了一位玩家选中的数字，那么这名玩家就会获得一个点，第一位获得 3 个点的玩家获胜。假设游戏在进行一段时间之后，数字 1 出现了两次（选择 1 的一方获得了两个点），而数字 5 只出现了一次（选择 5 的一方只获得了一个点），此时出于某种原因，游戏在这一刻被迫终止了，那么桌子上的 64 枚金币应当如何分配呢？

帕斯卡和费马给出了数学上的逻辑答案。假设游戏继续，如果那位已经有两个点的玩家在下一次掷骰子时赢了，那么全部的 64 枚金币就都属于他了；如果选择 5 的玩家在下一次掷骰子中赢了，那么二人就可以平均分配这 64 枚金币，每个人都得到 32 枚。

但是，如果双方都不再掷骰子，第一位玩家可能会争辩道：“就算我在下一次掷骰子时输了，我也会得到 32 枚金币。而对于余下的 32 枚金币，我有可能得到，你也有可能得到，机会是均等的。所以，应当把这 64 枚金币中我无论如何也会得到的那 32 枚先给我，然后再平均分配剩下的 32 枚金币。”换句话说，第一位玩家应当得到 48 枚金币，而另一位只能得到 16 枚。

难以置信，不是吗？一门全新的、反映了深刻思想的数学分支，就诞生于这类十分浅显，甚至有点微不足道的讨论之中！然而，这正是数学的有效性既“无理由”又神秘莫测的原因。

概率论的本质可以从以下这些简单的事实中看清楚。没有人能确定地预测出，一枚抛向空中的硬币在落地时哪一面会向上。即使是连续抛 10 次同一枚硬币，每次都是头像向上，也丝毫不能提高我们对第 11 次抛出的硬币是哪一面朝上的预测能力。

但是，如果把这枚硬币抛上一千万次，我们就可以精确地预测出，头像一面向上的次数非常接近一半，并且有字一面向上的次数也非常接近一半。事实上，在 19 世纪末，统计学家卡尔·皮尔森非常有耐心地连续抛了一枚硬币多达 24 000 次。

根据他的记录，抛出头像的次数是 12 012 次。在某种程度上，这就是概率论讲述的一切。概率论为我们提供了超多次试验的结果的精确信息，但不能预测任何特定的试验结果。如果一个试验有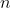种可能的结果，而且这几种可能结果发生的概率都是相同的，那么任何一个结果发生的概率就是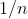。比如你掷一个骰子，那么出现数字 4 的概率是 1/6，这是因为一个骰子有 6 个面，而抛出任何一面的概率都是相同的。

设想一下，你连续掷 7 次骰子，每一次都得到 4，那么下一次你得到 4 的概率有多大？概率论给出了一个非常清楚的答案：仍然是 1/6。这是因为骰子没有记忆，任何“幸运之手”的说法或“下一次抛骰子会补偿先前抛掷过程中的不平衡（骰子各面出现的次数不同）”的观念都是妄想。事实真相是，如果你掷了 100 万次骰子，那么结果会平均分布，并且出现 4 的概率会非常接近 1/6。

我们再来看一个稍微复杂一点的例子。假设你一次同时抛 3 枚硬币，那么一个头像向上，另外两个字面向上的概率是多大？只需列举所有可能的结果，就能很容易得到答案。

如果我们把头像向上的一面定义为“H”，有字的一面定义为“T”，这样的话，就会有 8 种可能的结果：TTT、TTH、THT、THH、HTT、HTH、HHT、HHH。对照这 8 种结果，你会发现有 3 种情况与“一个头像、两个字面”的要求相符。因此，这一情况发生的概率是 3/8。在更一般的情况下，假设有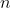种可能的基本结果，并且出现每种结果的机会都是均等的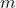，是你所感兴趣的事件数量，那么该事件发生的概率就是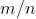。请注意，这就意味着概率总是 1 和 0 之间的某个值。

如果你所感兴趣的事件不可能发生，那么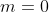（表示没有你喜欢的结果），而此时的概率值也是 0。另一方面，如果该事件绝对会发生，也就是说，所有的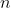种事件都是肯定的（），此时概率就是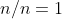。抛 3 枚硬币的试验结果还证实了概率论中的另一个重要结论：如果有多个事件，它们彼此是完全独立的，那么这些事件发生的概率是个体概率的产物。还是以同时抛 3 枚硬币为例，获得 3 个头像的概率是 1/8，其计算过程是这样的：因为抛一枚硬币得到头像的概率是 1/2，而抛 3 枚硬币时每枚硬币落地所得到的结果之间都是互相独立的，所以 1/2×1/2×1/2＝1/8。

你也许会想，除了在赌场或其他赌博活动中大显身手之外，这些基础的概率论概念还有什么其他用途吗？你可能无法想象，那些看起来并不是十分重要的定律正是现代遗传学（一门研究生物遗传特征的科学）的核心基础理论。

把概率论引入遗传学的是一位摩拉维亚牧师格莱格·孟德尔（Gregor Mendel，1824—1884）。孟德尔的家乡在一个小山谷中，这里紧邻摩拉维亚和西里西亚的交界（位于今天的捷克共和国）。孟德尔早年进入位于布尔诺的圣多默隐修院，之后，他在维也纳大学学习动物学、植物学、物理学和化学。

当孟德尔学成返回布尔诺，在圣多默隐修院院长的大力支持下，他用豌豆植株做实验，由此开始了遗传学研究。孟德尔使用豌豆做实验，主要是因为这种植物的容易生长，并且雌雄同体，这样一来，豌豆植株不仅能自花传粉，还能在其他植株间进行异花传粉。孟德尔让只结绿色种子的豌豆植株与只结黄色种子的豌豆植株进行异花传粉。

在之后的观察中，他得出了十分令人困惑的结果。从图 5-4 中可以看出，杂交后的第一代豌豆植株只产生黄色种子，然而在随后的第二代中，黄色种子和绿色种子的比例却是 3∶1 ！从这些令人惊讶的发现中，孟德尔总结出了三个基本规律，而这成了遗传学发展过程中最重要的里程碑。

(1) 生物某一特征的遗传与亲本传给后代的某种特定遗传“因子”（今天我们所熟知的基因）有关。

(2) 所有后代都会从每个亲本那里继承一项（针对任何给定特征的）“因子”。

(3) 一种给定特征也许不能在第二代中体现，却能传到第三代中。

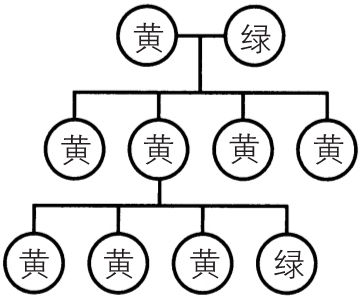
图　5 - 4

如何解释孟德尔实验中的数量关系？孟德尔认为，每一个亲本植株都一定有两个完全相同的“因子”，这就是今天所说的等位基因，等位基因要么是一对黄，要么是一对绿（图 5-5）。

当两株植物交配时，根据前述的规律 (2)，每一个后代都要从其父本和母本那里各继承一段不同的等位基因。也就是说，豌豆植株的每一个后代的种子都包含绿色的等位基因和黄色的等位基因。那么，为什么第二代的豌豆植株种子全部都是黄色的？

孟德尔的解释是，这是因为对于豌豆植株而言，黄色是占优势的颜色（显性性状），所以根据前述的规律 (3)，它把整个这一代中的绿色等位基因的显现给掩盖掉了。然而，依然是根据规律 (3)，占据优势的黄色并不能阻止隐性的绿色基因被遗传到下一代中。

在下一轮交配中，用包含黄色等位基因和绿色等位基因的植株与另一株同样包含这两等位基因的豌豆植株进行异花传粉。由于其后代分别从父本和母本那里各得到一段等位基因，因此它们的种子颜色将会呈现出图 5-5 所示的组合：绿绿、绿黄、黄绿、黄黄。由于黄色是占据优势的性状（显性性状），所以包含黄色等位基因的种子全都是黄色。同时，由于等位基本组合的概率是相同的，因此黄色种子的豌豆植株与绿色豌豆植株的比例是 3∶1。

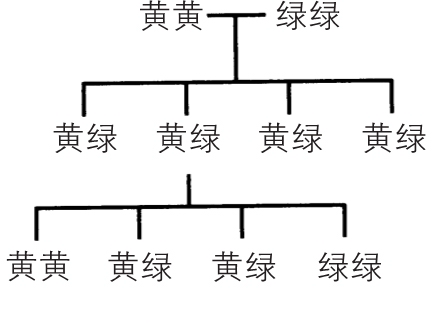
图　5-5

你也许已经意识到了，从本质上讲，孟德尔的整个实验与抛硬币是相同的。如果把硬币头像的一面视为绿色豌豆，把有字的一面视为黄色豌豆，要想知道豌豆呈现黄色的概率有多大（这里把黄色和字面作为显性性状），事实上，这与探讨在抛两枚硬币时至少得到一个字面朝上的概率有多大，是完全相同的。

很明显，答案是 3/4，因为在 4 种可能的结果里（字面 - 头像、字面 - 字面、头像 - 字面、头像 - 头像）至少有 3 次出现一个字面。这也就意味着，（在一段很长时间的实验后）在抛硬币时，至少出现一个字面向上的次数与完全不出现字面的次数的比例是 3∶1，这和孟德尔在实验中反映的结果完全一致！

孟德尔在 1865 年公开发表了他的论文《植物杂交实验》，并在两次科学会议上宣讲了他的实验结果，但是，他的研究成果没有获得人们的重视。直到进入 20 世纪后，孟德尔的实验才引起了人们的高度关注。虽然大家对其结论的精确性还有一些疑问，但孟德尔还是被视为历史上现代遗传学数学基础的奠基人。

沿着孟德尔指明的道路，英国著名统计学家罗纳德·艾尔默·费雪（Ronald Aylmer Fisher，1890—1962）建立了群体遗传学，这一数学分支确定了人群的基因分布模型，并计算了基因随时间的变化频率。今天，遗传学家们可以利用 DNA 组合中的统计采样来预测未出生后代可能的生理特征。但问题仍然存在：统计学和概率论究竟是怎么关联的？

事实和预测

期望破译宇宙演变奥秘的科学家通常会尝试同时从两个方向入手来解决问题。有些人从最初的宇宙中最微小的宇宙结构变化开始，有些人则研究当下这个宇宙状态的所有细节。前者使用大型计算机来模拟宇宙演变的进程，而后者采用了如侦探式的工作方式，力图从现在宇宙状态的大量事实中推演出宇宙的过去。

概率论和统计学的关系与宇宙学家们的研究模式十分相似：在概率论中，初始状态和变量是已知的，其目标是预测最可能出现的结果；而在统计学中，结果是已知的，但原因都是不确定的。

让我们分析一个简单的例子，来看看这两门学科是如何互相补充、相辅相成的——也可以说，它们是怎样中途相遇的。我们已经知道，统计学研究表明，大量的物理定量测量结果，甚至是人类的许多生理特征都是按照正态频率曲线的方式分布的。

更准确地说，正态曲线并不只是一根曲线，实际上，它是一簇曲线。这类曲线都可以用相同的通用数学公式来描述，而且，它们的外形特点仅需两个参量，就能完全刻画出来。第一个量是“均值”，也就是分布的平均值，以这个值为中心正态分布的曲线左右对称。当然，均值的实际大小还取决于测量变量的种类（如身高、体重、智商等）。甚至对同一变量而言，针对不同人群，均值也可能不同。举个例子，瑞典男人的平均身高可能与秘鲁男人的平均身高有差异。第二个定义了正态曲线的量为“标准差”。

标准差描述了数据在平均值周围的聚焦程度。在图 5-6 中，与其他两条曲线相比，可以看出曲线 a 的测量值是最分散的，这也就意味着，曲线 a 的标准差最大。均值和标准差引出了一个非常有趣的事实，那就是无论这两个参量的具体数值是多少，68.2% 的数据都落在了以平均值为中心、以标准差的数值为两侧边界的区间内。如果进行精确研究的话，若一个特定人群（人口数量足够大）的智商均值为 100，标准差值为 15，那么 68.2% 的人的智商将会在 85 至 115。

更进一步的研究表明，对于所有的正态分布曲线，95.4% 的数据落在以均值为中心、以 2 倍标准差数值为边界的区间内，99.7% 的数据落在以 3 倍标准差数值为边界的区间内。还是用刚才的那个案例来分析，95.4% 的人的智商值在 70 至 130，而 99.7% 的人的智商值在 55 至 145。

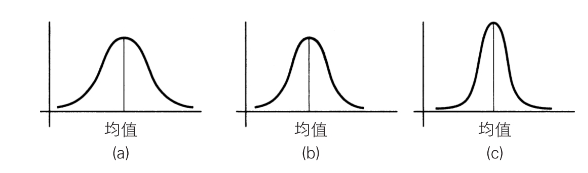
图　5-6

假设我们想预测，从人群中随机挑选出一个智商在 85 到 100 之间的人的概率有多大。图 5-7 告诉我们，概率为 0.341（34.1%），因为从概率论的定律我们知道，概率不过是想要的结果除以所有可能结果数量的商。如果我们还想知道从人群中随机挑选一个人，其智商高于 130 的概率，只看一眼图 5-7 就能说出答案，这种情况的概率仅有 0.022（2.2%）。

与此相似，利用正态分布的属性和积分（积分用来计算曲线的面积）这样的工具，我们能计算任何给定范围的智商概率。也就是说，概率论和它的合作伙伴统计学，联合起来为我们提供了答案。

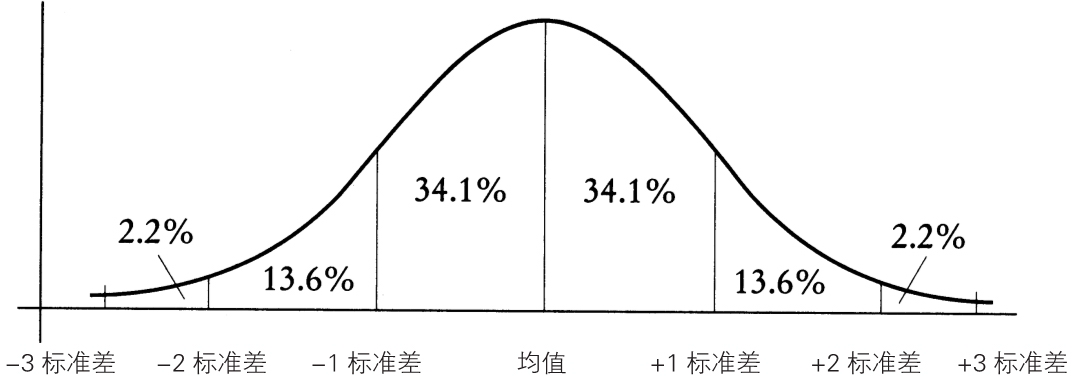
图　5-7

我在前面已经多次指出，概率论和统计学在处理大样本事件时才会有意义，它们从来不是用来解决个体问题的。这一基本认识就是著名的大数定理，雅各布·伯努利在他所著的《推测的艺术》一书中进行了系统的阐述（图 5-8 展示的是这本书在首版时的扉页）。

简而言之，大数定理表明，如果某一事件发生的概率是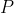，那么对于所有实验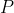，是事件发生最有可能的比例，而且如果实验次数接近无穷的话，那么事件发生的概率确定无疑就是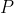了。伯努利在《推测的艺术》一书中这样介绍大数定理：“还需要进一步研究的是，增加观察次数能否让有利事件与不利事件的比例更接近真实的比例。”伯努利随后使用了一个特别的例子解释了这一概念：

“假设我们有一个罐子，里面有 3000 块白色的鹅卵石和 2000 块黑色的鹅卵石。假如我们事先并不知道这个罐子里究竟有多少块鹅卵石是黑色的，有多少块是白色的，而我们又想通过实验得出罐子里黑色与白色鹅卵石的比例，应当怎么做呢？

我们可以从罐子里一个接一个地取鹅卵石，并把每次取出的石头颜色记录下来，最后看看到底有多少次取出了黑色的鹅卵石，有多少次取出了白色的鹅卵石。（在这里，我要提醒的重要一点是，在取石头的过程中，当你取出一块鹅卵石并记录下颜色后，就应当把它放回到罐子里，然后再继续取，再放回去，这样，罐子中鹅卵石的数量就总是一个常数。）

现在我们要问，如果你能无限地取下去，例如次数为 10,100,1000,…，同时时间也是无限的（最终达到‘确实的确定’），那么，取出白色鹅卵石和取出黑色鹅卵石的比例数值是否与罐子中石头的实际比例相同呢？或者，这是另一个不同的数值？如果答案是不相同的话，那么我承认，要通过观察来确定每种情况发生的次数（如罐子中黑色鹅卵石与白色鹅卵石的数量），可能会失败。但是，如果我们能用这种方法实现‘确实的确定’……那么就能非常精确地断定一种后验情况发生的次数，就好像这是我们已知的一种先验情况。”

图　5-8

雅各布·伯努利花了 20 年时间来完善这一理论，而它最终成了统计学的支柱理论之一。伯努利认为，那些表面看上去只是碰运气的事情，事实上也遵循支配性的法则。他最终以这种信仰作为著作的结束语：

“如果持续不断地观察从现在直到永远发生的所有事情（因此，概率可能最终是确定的），我们就能发现，世界上所有的事情都有其必然的原因，并且绝对遵循某些确定的法则。所以说，我们自己，甚至那些看起来十分偶然的事件，都要受到某种自然规律的制约，而这似乎是命中注定的。我知道，柏拉图在关于宇宙循环学说中曾经提及这个观点，他认为，在经历了无穷的时间之后，所有事物都将会回到它们的本源状态。”

关于不确定性科学的故事，结局十分简单：数学在某些方面甚至可以应用在生活中那些不太“科学”的领域中，包括表面看来完全是由运气支配的领域。因此，在试图解释数学“无理由的有效性”时，我们不能把注意力仅仅局限在物理规律上。相反，我们最终可能不得不以某种方式弄清究竟是什么原因让数学无处不在。

数学那令人难以置信的力量在著名剧作家和散文作家乔治·萧伯纳（George Bernard Shaw，1856—1950）的笔下仍然颇具威力。萧伯纳绝对不是因为他的数学才能而闻名的，但是，他曾经写过一篇关于统计学和概率论的文章，这篇文章的观点极为深刻，题目为《赌博的邪恶和保险的美德》。在这篇文章里，萧伯纳承认，对他来说，保险是“建立在那些无法解释的事实，以及只有专业数学家才能计算的冒险的基础之上”。然而紧接着，他又写下了下面这段含义丰富的文字。

试想有一场商业谈判，一方是一位希望做国际贸易的商人，但他极度害怕会遭遇海难或被野蛮人给吃了；另一方是一位船长，他希望有大量的货物和乘客。船长回答商人，他的货物会十分安全，并且，如果他随船出海的话，他本人也同样安全。但是这位商人满脑子都是约拿、圣保罗、奥德修斯和鲁滨逊，不敢去冒险。他们之间的交流可能是这样的。

船长：放心！我保证，如果你乘坐我的船出海，明年的今天你还会好好地坐在这里。我可以和你打赌，赌注多少都行。

商人：但如果我和你打赌，我赌我在这一年里会死。

船长：你肯定会输的。你为什么不赌自己会活下来？

商人：但如果我被淹死了，同时你也会被淹死，那么我们还怎么赌？

船长：这样的话，我会找一个没有出海的人，他将和你的妻子及家人打赌。

商人：这改变了游戏规则。但是我的货物该怎么办？

船长：啧，这个赌也可以包括货物啊。或者我们打两个赌：一个是赌你的生命，另一个是赌你的货物。我向你保证，这两样都会很安全，什么意外都不会发生，而且你还会看到海外的瑰丽风光和奇观异景。

商人：但如果我和我的货物全部都安全的话，我还得额外再为我的生命和货物安全付给你一大笔钱。就算我没有被淹死，也会破产的。

船长：这的确是事实。对我来说，这笔钱并不像你想象的那么重要。如果你被淹死了，我可能是第一个被淹死的人，因为如果船沉了，我肯定是最后一个离开船并获救的人。无论如何，我还是劝你去冒个险。这样吧，我和你赌 10 倍的赌注，这能让你动心吗？

商人：嗯，这样的话……

这位船长已经认识到了保险的概念，正如金匠发现了银行的意义一样。

对某些人来讲，诸如萧伯纳，他们抱怨在自己所接受的教育中，“从来没有一个人就数学的意义或效用提过哪怕一个字”。而这段幽默的文字描述了关于保险的数学“历史”，很能说明问题。

到目前为止，除了萧伯纳的文章外，我们已经或多或少地透过数学家的眼睛看到了数学的某些分支的发展。对于这些人，以及如斯宾诺莎等众多理性主义哲学家而言，柏拉图主义是明摆着的事实。毫无疑问，数学真理存在于它们自己的世界，而且，人类思维仅仅通过推理的力量就能接近这些真理，而不用观察任何现象。

爱尔兰哲学家、克罗因的主教乔治·贝克莱（George Berkeley，1685—1753）第一个揭示了人类把欧几里得几何学作为普遍存在的真理的集合，与数学其他分支之间存在着某种潜在的差距。在他名为《分析者，或写给一位异教徒数学家的论文》的著作中（这里所说的异教徒一般被认为是埃德蒙德·哈雷），贝克莱从根本上批评了牛顿（在《原理》中）和莱布尼茨引入的微积分和分析法。贝克莱还证明了牛顿关于“流数”的概念（变化中的瞬时速度）没有经过严格的定义，在贝克莱的眼中，这足以让人们对其整个学科产生怀疑。

“流数方法是一把通用的钥匙，它帮助现代数学家解开了几何的奥秘，进而解开了自然界的奥秘……但是，这一方法到底是清晰还是晦涩，是始终如一还是前后矛盾，是结论性的还是证据不足，如果说我的态度不够公允的话，那么我把这个疑问交给最公正的读者们来判断吧。”

贝克莱的确认识到了这个问题。事实上，关于分析学的一致性理论直到 20 世纪 60 年代才真正形成。但是，数学家在 19 世纪却经历了一场极具戏剧性的大转折。