Math-Ug-1a-Pasw-007-三角函数及其属性

前篇：角的弧度表示

三角函数及其属性

我们假设你已经掌握初级三角学中，正锐角的sine，cosine和tangent定义（对比斜，邻比斜，对比邻）。
我们现在要把这个定义推广到大于$90°$的角和负角上去。
提前说好，除非特殊标明，下文中所有角的度量都采用弧度制。

极角的定义

看下图：

设$X$是$x$轴正方向上任一点。
如果我们取线段$OX$，绕端点$O$逆时针旋转，到达一个终末位置，记为线段$O{X}^{\prime }$，旋转过程中形成的角视为正。
如果顺时针旋转，则角视为负。
这些角在量值（不带单位和符号的数值）上是无限的。
我们把这种从x轴正方向开始测量的角叫做极角（polar angle）。
以$O{X}^{\prime }$为终末位置的角有无限个，它们之间的区别是量值相差整数个$2\pi$。

三角函数的定义

看图说话：

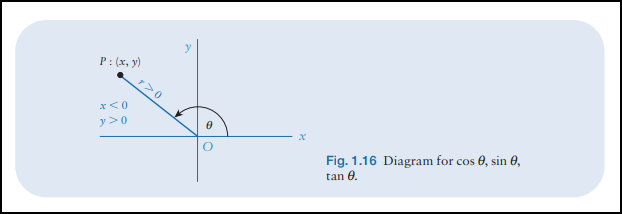
所有角的三角函数sine，cosine和tangent都按上图中标出的东西来定义：$P:(x,y)$是任一点，$\theta$是一个极角。
$OP$的长：
$$OP=r=\sqrt{x^2+y^2}>0$$
万事俱备，我们终于可以给出任意角$\theta$三角函数的定义：

如果四个象限分开来看，上述定义都是初级三角学中sine，cosine和tangent定义的拓展（从$P$点向$x$轴作垂线，得直角三角形）。
$r$始终是正的，对应直角三角形里的斜边长。
但$x,y$从三角形里对边，邻边长的正值，变成了坐标系里可正可负的带符号值。
进而决定了sine，cosine和tangent的正负。

• 第一象限：$x>0,y>0$: 都$>0$
• 第二象限：$x<0,y>0$: 只有$sin\theta >0$
• 第三象限：$x<0,y<0$: 只有$tan\theta >0$
• 第四象限：$x>0,y<0$: 只有$cos\theta >0$

为了便于表示和计算，我们通常令 $r=1$，这样可以直接得到不带 $r$ 的函数值。

三角函数$\sin \theta ,\cos \theta$的图象

1. $sin\theta$和$cos\theta$的图象形状相同，但是在$x$轴方向上相差$\frac{1}{2}\pi$。
   它们的关系是：
   $$\sin \theta =\cos (\theta -\frac{1}{2}\pi ),\cos \theta =\sin (\theta +\frac{1}{2}\pi )$$
2. 这两个函数都是周期函数，周期或者波长是$2\pi$；意思是曲线每隔$2\pi$这个长度就重复自身的形状。
   结合我们之前讲的极角，这很好理解，$2\pi$就是极角转过一整个圆，无论是逆时针转还是顺时针转，终止边都在同一个位置。
3. $\cos \theta$是一个偶函数，所以$\cos \theta =\cos (-\theta )$；$\sin \theta$是一个奇函数，所以$-\sin \theta =\sin (-\theta )$；
4. 两个函数的函数值在$\pm 1$之间振荡。

三角函数$\tan \theta ,\cot \theta ,\sec \theta ,\csc \theta$的图象

一些三角函数公式

高中学的

1. 和差化积
2. 积化和差
3. 倍角半角
4. 余弦公式
5. 正弦公式（这个没印象了）

简谐函数

我们目前遇到的都是$cos\theta$，$sinA$，无论是$\theta$还是$A$都是限制在几何上下文中的确定的角，但应用在其他领域的三角函数和几何角并没有关系。
举个例子，比如$cos\omega t$这样的表达式，$t$代表时间，$\omega$代表另一个常量。
无论上下文是什么，等式都成立。

遵循这种思想，我们得到一个重要的等式，它揭示了任何函数都具有$a\cos u+b\sin u$的形式，$u$是自变量，$a$和$b$是常量。
上式可以改写成$c\cos (u+\varphi )$的形式，$c$和$\varphi$是常量，它们用$a,b$表示：

改写过程如下：
首先有
$$c=\sqrt{a^2+b^2}>0$$
然后我们重写$a\cos u+b\sin u$：
$$a\cos u+b\sin u=c[(\frac{a}{c})\cos u+(\frac{b}{c})\sin u]$$
最后令$\varphi$等于满足以下条件的角：
$$cos\varphi =\frac{a}{c}andsin\varphi =-\frac{b}{c}$$

结合上图，我们发现$\varphi$可以由$Q:(a,-b)$结合原点与$x$轴来构造。
以此位置为终止边的任一极角都满足上述条件；我们选择量值最小的角。
（放到极坐标系里，$c$就是极轴长,$\varphi$就是极角）。
最终我们得到：
$$a\cos u+b\sin u=c[\cos \varphi \cos u-\sin \varphi \sin u]=c\cos (u+\varphi )$$

通过角，将极坐标系和直角坐标系联系到一起？
具有$A\cos (ku+\alpha )$形式，$A,k,\alpha$是任何常量，叫做简谐函数或变量为$u$的正弦曲线。
我们也可以改写成$A\sin (ku+\alpha +\frac{\pi }{2})$的形式。

考虑如下简谐函数：
$$y=c\cos (\omega t+\varphi )(c>0)$$
t表示时间。
这个函数的因变量$y$随着像规则波一样变化的时间而变化（如果距离x代替时间t作为变量，也可以说随着距离变化）。

曲线的整体形状和$c\cos t$相同，但沿$t$轴向左平移了$\frac{\varphi }{\omega }$，整体周期也拉伸或压缩，取决于$\omega$。$\omega >0$压缩；$\omega <0$拉伸。
曲线以$\frac{2\pi }{\omega }$为周期重复，由此得到等式：
$$y=c\cos [\omega (t+\frac{2\pi }{\omega })+\varphi ]=c\cos (\omega t+2\pi +\varphi )=c\cos (\omega t+\varphi )$$
函数的每部分都有它的定义：
$c>0$叫做振幅（amplitude）；$y$是在$\pm c$之间振荡（oscillate）。
频率（frequency） 是单位时间循环的次数，是$\frac{\omega }{2\pi }$，$\omega$叫做角频率（circular and angular frequency）。
$\varphi$叫做相位角（phase angle） 或 初相角。

以$p$为周期的周期函数的一般形式是$f(x+p)=f(x)$，对任意$x$都成立。
如果$p$为周期，那么显然$2p,3p$…都是周期。
我们一般说的周期，是最小正周期 $p$。

自测题

$$\begin{array}{rl}\cos \frac{\pi }{12}& =\sqrt{\frac{1+\cos \frac{\pi }{6}}{2}}\\ & =\sqrt{\frac{1+\frac{\sqrt{3}}{2}}{2}}\end{array}$$
$$\begin{array}{rl}\sin \frac{\pi }{12}& =+\sqrt{\frac{1-\cos \frac{\pi }{6}}{2}}\\ & =+\sqrt{\frac{1-\frac{\sqrt{3}}{2}}{2}}\end{array}$$

harmonic：capable of expression in the form of sine and cosine functions（mathematics term）；
of or concerned with an oscillation that has a frequency that is an integral multiple of a fundamental frequency（physics term）

后篇：逆函数