沃尔什函数 与 沃尔什-哈达玛变换

 

图像处理中有许多变换常常选用方波信号或者它的变形。

沃尔什函数是一组矩形波，其取值为1和-1，非常便于计算机运算。

沃尔什函数有三种排列或编号方式，以哈达玛排列最便于快速计算。

采用哈达玛排列的沃尔什函数进行的变换称为沃尔什-哈达玛变换，简称WHT或直称哈达玛变换。

 

沃尔什函数

沃尔什函数有三种不同的函数定义，但都可由拉德梅克函数构成。

1、按沃尔什排列的沃尔什函数

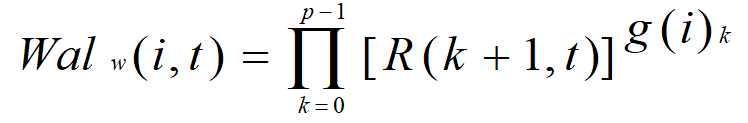
其中，R(k+1,t)是任意拉德梅克函数，g(i)是i的格雷码， g(i)k是此格雷码的第k位数。P为正整数，

 

取样后得到的按沃尔什排列的沃尔什函数矩阵：

2、按佩利（Paley）排列的沃尔什函数

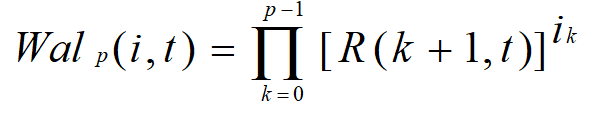
其中，R(k+1,t)是任意拉德梅克函数，ik是自然二进制码的第k位数。P为正整数，。    

取样后得到的按佩利排列的沃尔什函数矩阵：     

 

3、按哈达玛（Hadamard）排列的沃尔什函数

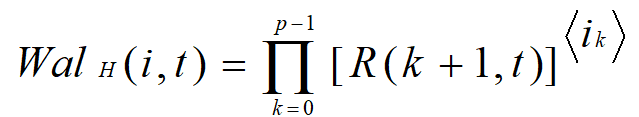
其中，R(k+1,t)是任意拉德梅克函数，<ik>是倒序的二进制码的第k位数。P为正整数，。        

取样后得到的按哈达玛排列的沃尔什函数矩阵：

   

2^n阶哈达玛矩阵有如下形式：

 

可见，哈达玛矩阵的最大优点在于它具有简单的递推关系， 即高阶矩阵可用两个低阶矩阵的克罗内克积(Kronecker Product)求得。因此常采用哈达玛排列定义的沃尔什变换。

 

离散沃尔什－哈达玛变换（DWHT）

      

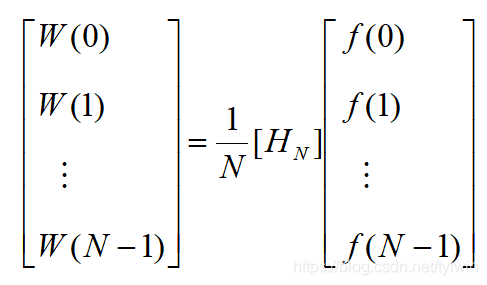
式中，［Hn］为N阶哈达玛矩阵。

由哈达玛矩阵的特点可知，沃尔什-哈达玛变换的本质上是将离散序列f(x)的各项值的符号按一定规律改变后，进行加减运算， 因此，它比采用复数运算的DFT和采用余弦运算的DCT要简单得多。

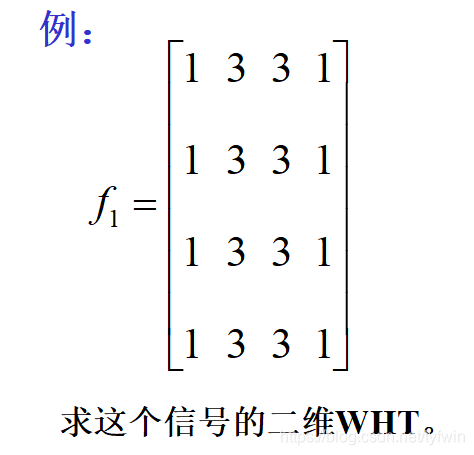
从以上例子可看出，二维WHT具有能量集中的特性，而且原始数据中数字越是均匀分布，经变换后的数据越集中于矩阵的边角上。因此，二维WHT可用于压缩图像信息。

 

快速沃尔什变换（FWHT）

类似于FFT，WHT也有快速算法FWHT， 也可将输入序列f(x)按奇偶进行分组，分别进行WHT。FWHT的基本关系为：

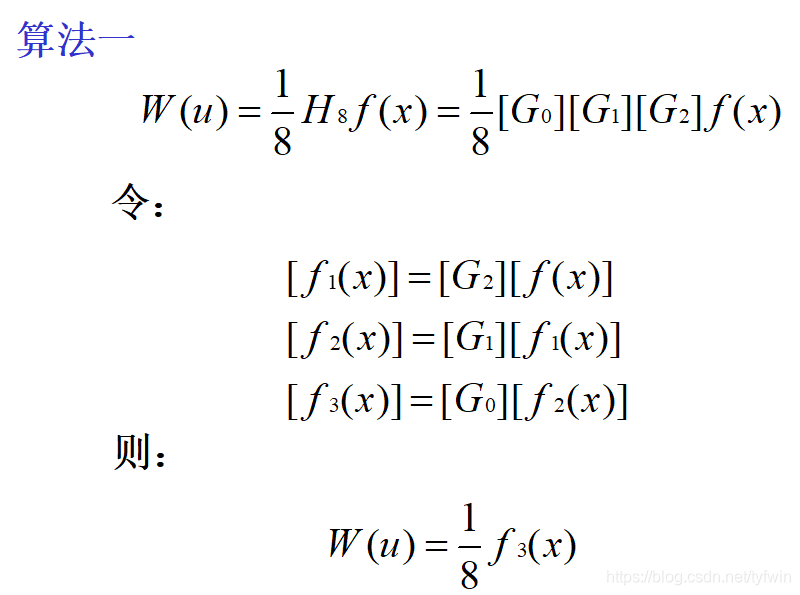
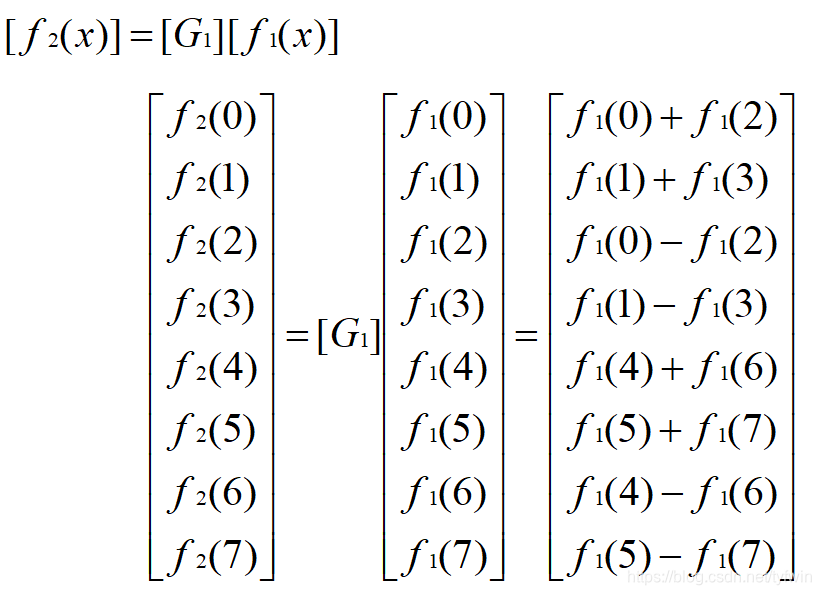
WHT是将一个函数变换成取值为＋1或－1的基本函数构成的级数，用它来逼近数字脉冲信号时要比FFT有利。同时， WHT只需要进行实数运算，存储量比FFT要少得多， 运算速度也快得多。因此，WHT在图像传输、 通信技术和数据压缩中被广泛使用。