STL中的RB-tree

set和map的底层结构都是红黑树，它们最后基本只是对红黑树接口的简单调用。

这里就主要来说一说红黑树。

1.红黑树的定义

红黑树首先是一棵二叉搜索树（BST），二叉的意思是每个节点最多有两个儿子，搜索的意思是根节点大于左儿子，小于右儿子。

在此基础上还要满足以下5个条件：

（1）只有红色和黑色2种节点

（2）根节点为黑色

（3）父子节点不能同时为红色

（4）任意节点，到达其叶子节点的所有路径包含的黑色节点个数相同

（5）空节点看作黑色节点

个人感觉整个红黑树最重要的部分就是先理解这个定义，看看它到底要告诉我们什么？为什么要这么做？下面我就来说说我的理解。

（1）只有红色和黑色2种节点

这一条很好理解，既然叫红黑树，那么就是将这种BST中的节点分为了2种，一种是红色节点，一种是黑色节点。

（3）父子节点不能同时为红色

这一条是对红色节点的限制，这样就保证了要加入红色节点必须加一层红色再加一层黑色，这样就保证了N黑>=N红

（4）任意节点，到达其叶子节点的所有路径包含的黑色节点个数相同

这一条是对黑色节点的限制，这样就保证了，单独看黑色节点的话，红黑树是一棵完美黑色平衡的树。

（3）、（4）节点合起来究竟要表达什么呢？

我的结论是，对于搜索性能的保证。

根节点到任意叶子节点的最长路径长度：N黑1+N红

根节点到任意叶子节点的最短路径长度：N黑2

由（3）可知，N红<=N黑

由（4）可知，N黑1=N黑2=N黑

所以最长长度<=最短长度*2

而一棵与红黑树节点总数相等的完全平衡树，其高度必定介于红黑树最长长度和最短长度之间。

那么红黑树的搜索效率必定至少是完全平衡树的一半。

（2）根节点为黑色

通过之后我们认识到，新加入的节点必定要为红色，因为如果为黑色，必定就破坏了条件（4），因为平白无故增加了一个黑色节点。

这个时候又要保证条件（3），那么就需要进行一些父子节点的颜色交换，将父亲变红，将儿子变黑。见后文3.（3）变色与旋转

这样可能导致红色不停地向上传递，最终传递到根节点，这个时候根节点会自己变为红色，然后将儿子设定为黑色。

然后每次插入结束，再把根节点置为黑色。如果一开始根节点就为红色，这种变化就完不成。

（5）空节点看作黑色节点

这个在插入节点要进行的旋转操作中可以看到，父亲和儿子同为红色旋转的时候，叔叔节点为红色是一种情况，叔叔节点为空或者为黑色是一种情况。

也就是说，节点为空和为黑色，可以当做一种情况来处理，所以空节点看作黑色节点也是理所当然的。

总结一下：

条件（2）保证了，条件（3）、（4）的成立

条件（3）、（4）才是最重要的条件，因为它们共同保证了，红黑树的搜索效率。

2.迭代器的移动

说到红黑树的迭代器，就不得不先说一下stl红黑树实现的时候的内部结构。

直接上图

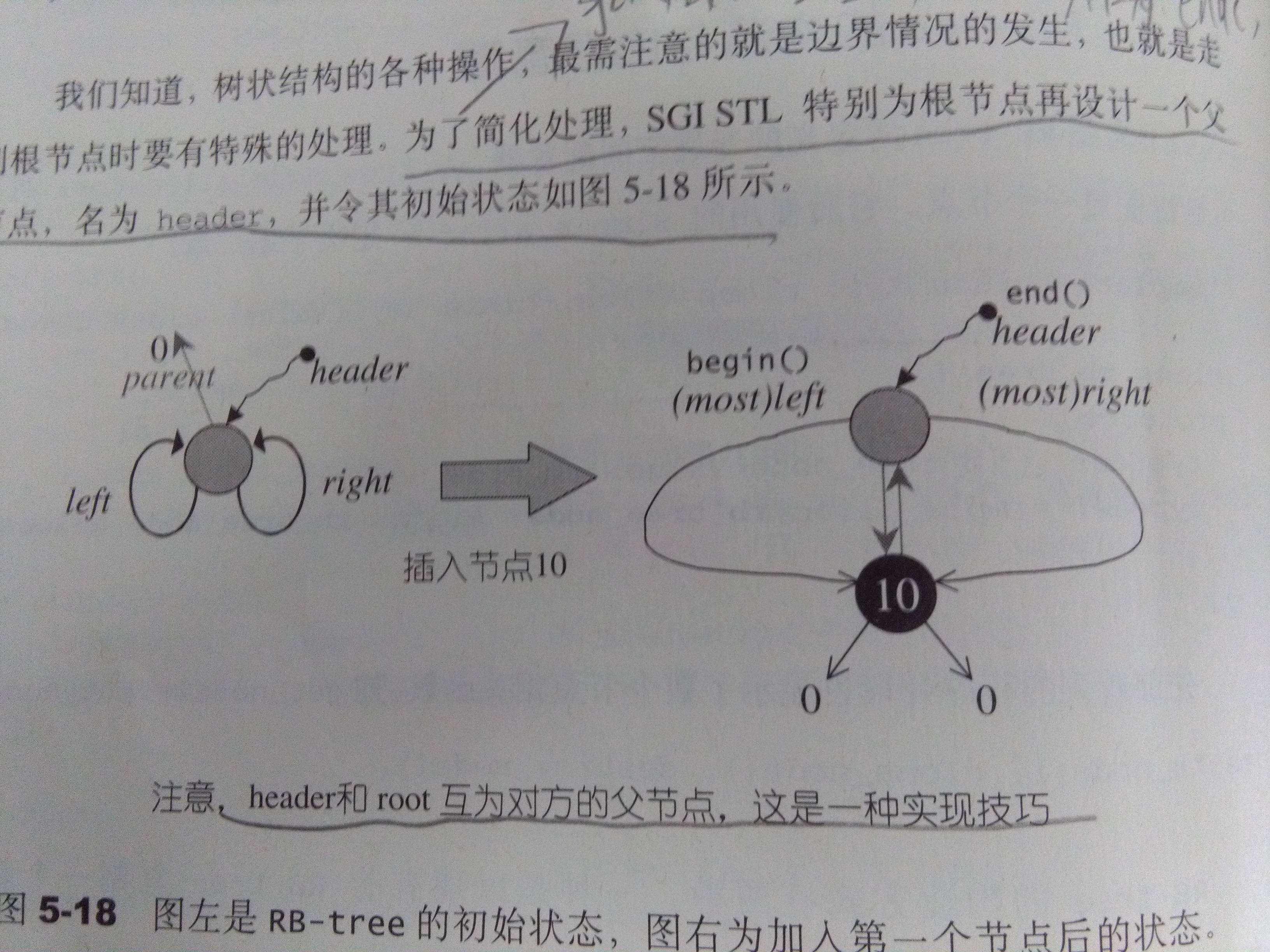
在root节点之上还有一个header节点，这个节点可以看做是end节点。

它的left指向全树最小节点，用leftmost表示，同时它也是begin节点。

它的right指向全树最大节点，用rightmost表示。

header节点的父节点是root，同时root节点的父节点是header。

父节点的父节点是本身，并且是红色的就是header节点。

父节点的父节点是本身，并且是黑色的就是root节点。

header节点的引入是为了方便管理，使得迭代器符合[begin, end)规则。

迭代器的移动，也是要按着节点增大那样来移动。

下面说说边界情况。

①increment

++rightmost = end

++end 结果不确定,但是肯定是rb-tree中的节点

②decrement

--leftmost = end

--end = rightmost

3.插入节点

这里只讨论插入的节点是均不相同的情况。

（1）函数调用

insert_unique ==》 __insert ==》 __rb_tree_rebalance 

==》__rb_tree_rotate_left

==》__rb_tree_totate_right

（2）最终的处理

就是穷举了所有的情况，然后按照不同的情况来处理。

（3）变色与旋转

由之前的条件（4）可知，新加入的节点肯定是红色的，

①如果父亲是黑色，什么都不用做。

②如果父亲是红色，那么爷爷肯定是黑色，这个时候如果叔叔存在且也为红色，这个时候只需要将父亲和叔叔都变为黑色，然后将爷爷变为红色。

然后再往上迭代检查，最后将根节点置为黑色。

③如果父亲是红色，那么爷爷肯定是黑色，这个时候如果叔叔存在且为黑色或者叔叔不存在，就需要旋转。

旋转的时候也需要变色，以保证条件（4）。

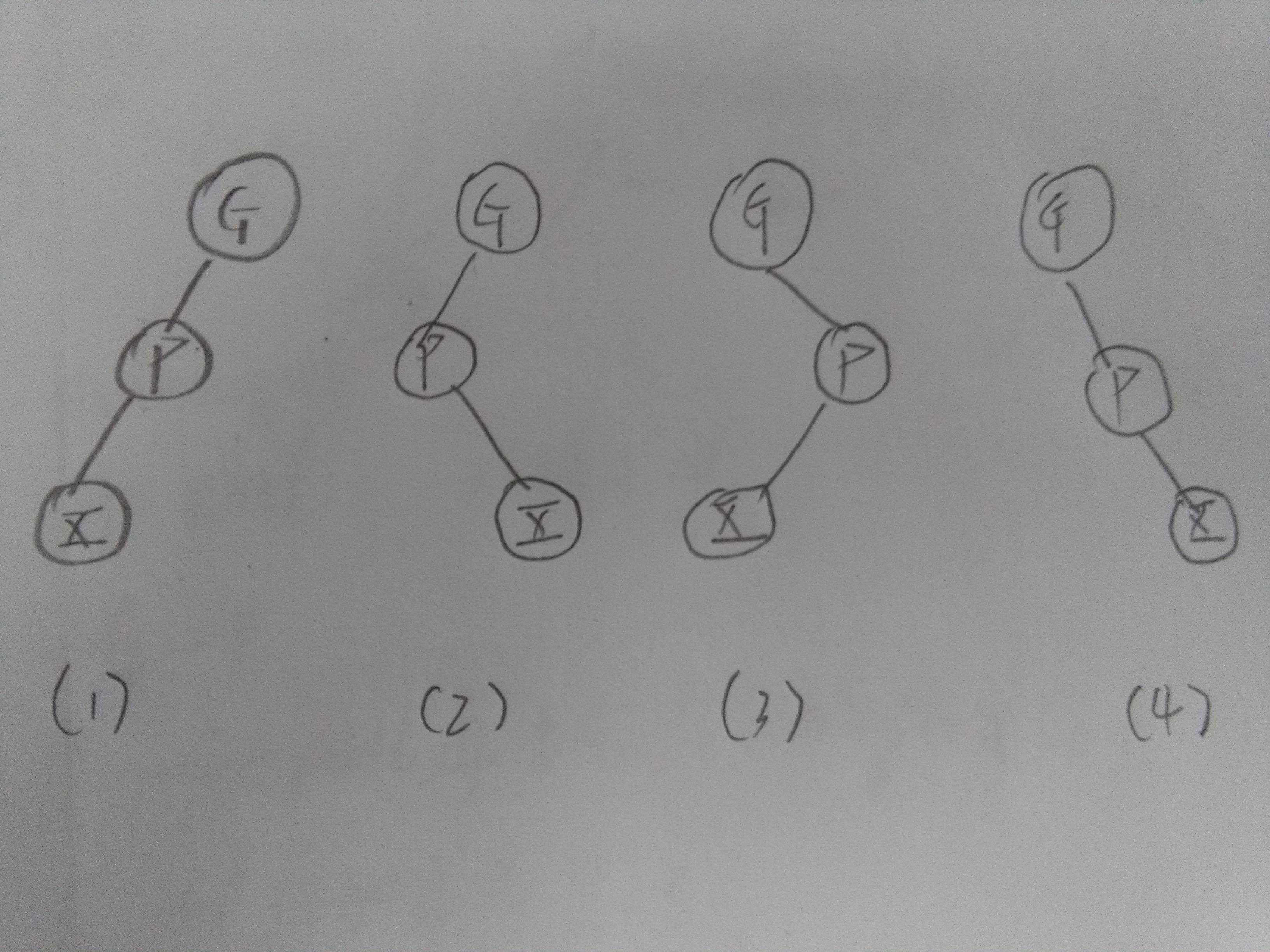
（4）单旋转与双旋转

之所以会存在单、双旋转是因为，在旋转的过程中还必须首先保持红黑树是一棵BST，也就是说，根节点大于左节点且小于右节点。

（1）和（4）中间大小的节点恰好是P，所以单旋转就好。

（2）和（3）中间大小的节点却是X，所以需要双旋转。

所以红黑树的插入操作最多需要2次旋转。旋转复杂度为O（1）

（5）左旋转与右旋转

①左旋转

左子节点顶替父亲的位置，父亲作为原左子节点的右子节点

②右旋转

右子节点顶替父亲的位置，父亲作为原右子节点的左子节点