数据结构

最新推荐文章于 2024-11-18 21:25:45 发布

梦醒-已千年

最新推荐文章于 2024-11-18 21:25:45 发布

阅读量506

点赞数

分类专栏：数据结构算法文章标签：数据结构算法

本文链接：https://blog.csdn.net/u010102951/article/details/44491223

版权

这篇博客探讨了计算模型，包括图灵机模型和RAM模型，以及算法的时间复杂度分析，使用大O记号表示算法效率。还讨论了算法设计策略，如递归、动态规划，并通过MaxTwo问题举例说明了分治法的应用。此外，文章提到了斐波那契数列在动态规划中的应用和计算问题。

摘要由CSDN通过智能技术生成

计算模型

图灵机模型

这里写图片描述

Tape：纸带。依次均匀地划分单元格，各含有某一个字符，默认为“#”。
Alphabet：字母表。字符的种类有限。
Head：读写头。总是对准某一个单元格，并可以读取和改写其中的字符，每经过一个节拍，可以转向左侧或者右侧的邻格。
State:状态。TM（Turning Machine）总是处于有限状态中的某一种，每经过一个节拍，可以按照规则（状态转换函数）转向另一种状态。
Transaction Function：（q,c;d,L/R,p）状态转换函数是一个5元组，q表示图灵机或者读写头当前的状态，c表示读写头当前指向的单元格的里的字符，这两项可以理解为当前的状态；后面3项描述它紧接着的动作，d表示在当前单元格填入或者修改成的一个新的字符，在修改完毕之后读写头可以向左（L）或者向右（R）移动一个单元格，同时将自己的状态由刚刚是q转换为现在的p。一旦进入特定的状态h，则停机。

RAM模型

Random Access Machine。从计算的情况下讲，它和图灵机是完全对等的，和图灵机一样二者都拥有无限的空间。

寄存器顺序编号，总数没有限制。r0，r1，r2……
每一基本操作仅需要常数时间（循环和子程序不是基本操作）。

例如：直接将常数赋值给寄存器、寄存器间接取址、加减法、判断语句、无条件跳转、停止语句STOP和图灵机中的停机状态h完全对等。

运用以上的计算模型实际上完成了算法的运行时间到算法执行的基本次数的转换。脱离的程序的具体运行平台，使得算法的评判更加客观。

大O记号

渐进分析：当n>>2（足够大）后，对于规模为n输入，算法需要执行的基本操作次数：T(n) = ?，需要占用的存储单元S(n) = ?（通常可以不考虑）。

T(n) = O(f(n)) iff 存在 c > 0，当n >> 2后有T(n) < c·f(n)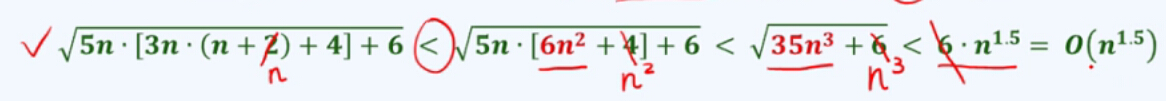

这里写图片描述
和T(n)相比，f(n)更加简洁，但是仍然反映前者的增长趋势。

常系数可以忽略。O(f(n)) = O(c·f(n))
低次项可以忽略。O(n^a + n^b) = O(n^a) , a > b >0

其他符号
这里写图片描述

高效解

O(1)常数复杂度。例如：2 = 2015 = 2015 * 2015 = 2015^2015 = O(1)，这一类的算法效率最高。

没有循环
没有分支
没有递归
不含跳转
以上的代码必然是顺序执行，时间复杂度为O(1)。

O(logN)对数多项式复杂度
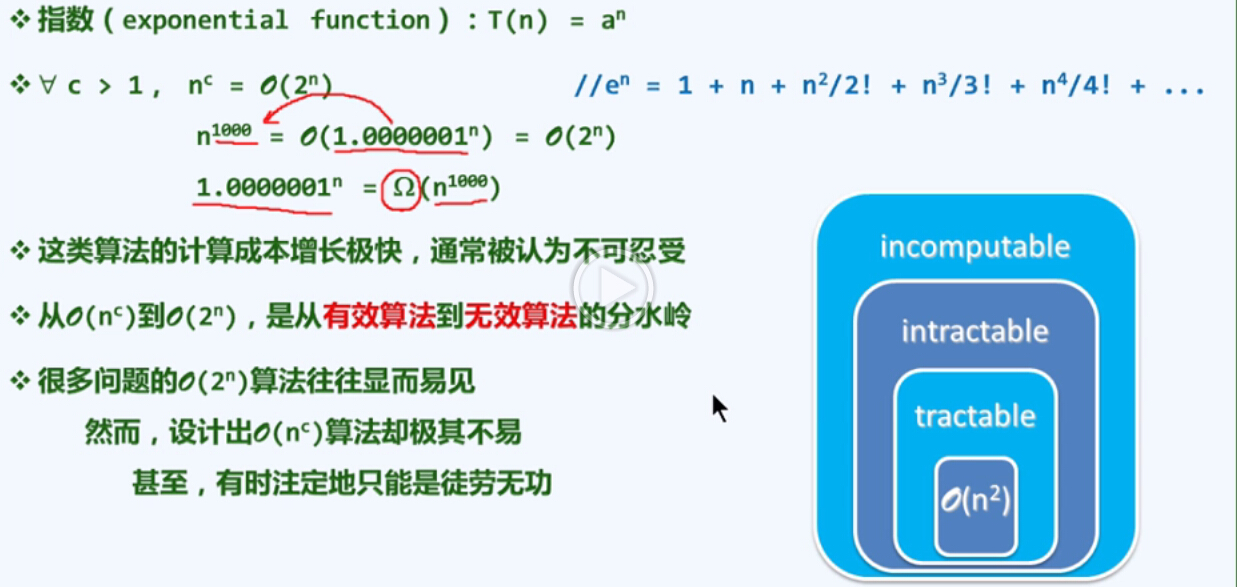
这里写图片描述

有效解

这里写图片描述

难解

这里写图片描述
这类算法增长速度太快，我们通常认为是不可忍受的。

算法分析

级数

算术级数——与末项平方同阶
T(n) = 1 + 2 + 3 + …… + n = n·(n + 1) / 2 = O(n^2)

幂方级数——比幂高出一阶
T(n) = 1^2 + 2^2 + 3^2 + …… + n^2 = n·(n + 1)( n + 2) / 6 = O(n^3)
T(n) = 1^3 + 2^3 + 3^3 + …… + n^3 = n^2·(n + 1)^2 / 4 = O(n^4)
T(n) = 1^4 + 2^4 + 3^4 + …… + n^4 = n·(n + 1)·(2n + 1)·(3^2 + 3·n -1) / 30 = O(n^5)

几何级数——与末项同阶
T(n) = a^0 + a^1 + a^2 + …… + a^n = (a^(n+1) - 1) / (a -