DSA和ECDSA算法

最新推荐文章于 2024-08-15 18:07:10 发布

The_Hungry_Brain

最新推荐文章于 2024-08-15 18:07:10 发布

阅读量6.5k

点赞数 3

分类专栏：密码学 OpenSSL 数论

本文链接：https://blog.csdn.net/u010129119/article/details/62423036

版权

OpenSSL 同时被 3 个专栏收录

10 篇文章 1 订阅

订阅专栏

密码学

8 篇文章 1 订阅

订阅专栏

数论

6 篇文章 0 订阅

订阅专栏

关键词：

DSA：Digital Signature Algorithm (DSA)

ECDSA：The Elliptic Curve Digital Signature Algorithm (ECDSA)

DSS：Digital Signature Standard (DSS)

NIST：(U.S. National) Institute of Standards and Technology

FIPS：(U.S. Government) Federal Information Processing Standard

离散对数问题：discrete logarithm problem

欧拉函数：Φ(n)

欧拉定理：

主要内容：

密钥生成。key generation

签名生成。signature generation

签名验证。signature veri cation

1、DSA

密钥生成

1）、选择一个素数 q ，使得 2¹⁵⁹ < q< 2¹⁶⁰

2）、选择一个 1024-bit 的素数 p，属性为 q | p - 1。

（DSS 强制要求 p 是一个素数，使得 2^511+64t < q< 2^512+64t，当0 ≤ t ≤ 8。如果 t = 8，则 p 是一个 1024-bit 的素数。）

3）、选择一个元素 h ，h介于[ 1， p-1 ]，然后计算 g = h^{(p- 1)/q}mod p。重复直到 g ≠ 1。

4）、选择一个随机整数 x 在 [ 1，q - 1 ]。

5）、计算 y= g^x mod p

6）、公钥是：（p，q，g，y）；私钥是 x 。

对应openssl源码：

static int dsa_builtin_keygen(DSA *dsa)
{
    int ok = 0;
    BN_CTX *ctx = NULL;
    BIGNUM *pub_key = NULL, *priv_key = NULL;

    if ((ctx = BN_CTX_new()) == NULL)
        goto err;

    if (dsa->priv_key == NULL) {
        if ((priv_key = BN_secure_new()) == NULL)
            goto err;
    } else
        priv_key = dsa->priv_key;

    do
        if (!BN_rand_range(priv_key, dsa->q))
            goto err;
    while (BN_is_zero(priv_key)) ;

    if (dsa->pub_key == NULL) {
        if ((pub_key = BN_new()) == NULL)
            goto err;
    } else
        pub_key = dsa->pub_key;

    {
        BIGNUM *prk = BN_new();

        if (prk == NULL)
            goto err;
        BN_with_flags(prk, priv_key, BN_FLG_CONSTTIME);

        if (!BN_mod_exp(pub_key, dsa->g, prk, dsa->p, ctx)) {
            BN_free(prk);
            goto err;
        }
        /* We MUST free prk before any further use of priv_key */
        BN_free(prk);
    }

    dsa->priv_key = priv_key;
    dsa->pub_key = pub_key;
    ok = 1;

 err:
    if (pub_key != dsa->pub_key)
        BN_free(pub_key);
    if (priv_key != dsa->priv_key)
        BN_free(priv_key);
    BN_CTX_free(ctx);
    return (ok);
}

签名生成

1）、选择一个随机整数 k ，k 介于[ 1，q - 1 ]。

2）、计算 r = (g^k mod p) mod q。

3）、计算 k^-1 mod q。

4）、计算 s = k^-1 {h(m) + xr} mod q，h 是安全哈希算法（SHA-1）。

5）、如果 s = 0，则转到步骤 1）。

6）、签名信息 m 是 r 和 s 的组合（r，s）。

对应openssl中源码：

static DSA_SIG *dsa_do_sign(const unsigned char *dgst, int dlen, DSA *dsa)
{
    BIGNUM *kinv = NULL;
    BIGNUM *m;
    BIGNUM *xr;
    BN_CTX *ctx = NULL;
    int reason = ERR_R_BN_LIB;
    DSA_SIG *ret = NULL;
    int rv = 0;

    m = BN_new();
    xr = BN_new();
    if (m == NULL || xr == NULL)
        goto err;

    if (!dsa->p || !dsa->q || !dsa->g) {
        reason = DSA_R_MISSING_PARAMETERS;
        goto err;
    }

    ret = DSA_SIG_new();
    if (ret == NULL)
        goto err;
    ret->r = BN_new();
    ret->s = BN_new();
    if (ret->r == NULL || ret->s == NULL)
        goto err;

    ctx = BN_CTX_new();
    if (ctx == NULL)
        goto err;
 redo:
    if (!dsa_sign_setup(dsa, ctx, &kinv, &ret->r, dgst, dlen))
        goto err;

    if (dlen > BN_num_bytes(dsa->q))
        /*
         * if the digest length is greater than the size of q use the
         * BN_num_bits(dsa->q) leftmost bits of the digest, see fips 186-3,
         * 4.2
         */
        dlen = BN_num_bytes(dsa->q);
    if (BN_bin2bn(dgst, dlen, m) == NULL)
        goto err;

    /* Compute  s = inv(k) (m + xr) mod q */
    if (!BN_mod_mul(xr, dsa->priv_key, ret->r, dsa->q, ctx))
        goto err;               /* s = xr */
    if (!BN_add(ret->s, xr, m))
        goto err;               /* s = m + xr */
    if (BN_cmp(ret->s, dsa->q) > 0)
        if (!BN_sub(ret->s, ret->s, dsa->q))
            goto err;
    if (!BN_mod_mul(ret->s, ret->s, kinv, dsa->q, ctx))
        goto err;

    /*
     * Redo if r or s is zero as required by FIPS 186-3: this is very
     * unlikely.
     */
    if (BN_is_zero(ret->r) || BN_is_zero(ret->s))
        goto redo;

    rv = 1;

 err:
    if (rv == 0) {
        DSAerr(DSA_F_DSA_DO_SIGN, reason);
        DSA_SIG_free(ret);
        ret = NULL;
    }
    BN_CTX_free(ctx);
    BN_clear_free(m);
    BN_clear_free(xr);
    BN_clear_free(kinv);
    return ret;
}

签名验证

1）、获取公钥（p，q，g，y）的真实副本。

2）、验证 r 和 s 是否为整数，且介于区间[ 1，q - 1 ]。

3）、计算 w = s^-1 mod q 以及 h(m)。

4）、计算 u1 = h(m)w mod q 以及 u2 = rw mod q。

5）、计算 v = (g^u1 y^u2 mod p) mod q

6）、当且仅当 v = r，签名验证正确。

对应openssl源码：

static int dsa_do_verify(const unsigned char *dgst, int dgst_len,
                         DSA_SIG *sig, DSA *dsa)
{
    BN_CTX *ctx;
    BIGNUM *u1, *u2, *t1;
    BN_MONT_CTX *mont = NULL;
    const BIGNUM *r, *s;
    int ret = -1, i;
    if (!dsa->p || !dsa->q || !dsa->g) {
        DSAerr(DSA_F_DSA_DO_VERIFY, DSA_R_MISSING_PARAMETERS);
        return -1;
    }

    i = BN_num_bits(dsa->q);
    /* fips 186-3 allows only different sizes for q */
    if (i != 160 && i != 224 && i != 256) {
        DSAerr(DSA_F_DSA_DO_VERIFY, DSA_R_BAD_Q_VALUE);
        return -1;
    }

    if (BN_num_bits(dsa->p) > OPENSSL_DSA_MAX_MODULUS_BITS) {
        DSAerr(DSA_F_DSA_DO_VERIFY, DSA_R_MODULUS_TOO_LARGE);
        return -1;
    }
    u1 = BN_new();
    u2 = BN_new();
    t1 = BN_new();
    ctx = BN_CTX_new();
    if (u1 == NULL || u2 == NULL || t1 == NULL || ctx == NULL)
        goto err;

    DSA_SIG_get0(sig, &r, &s);

    if (BN_is_zero(r) || BN_is_negative(r) ||
        BN_ucmp(r, dsa->q) >= 0) {
        ret = 0;
        goto err;
    }
    if (BN_is_zero(s) || BN_is_negative(s) ||
        BN_ucmp(s, dsa->q) >= 0) {
        ret = 0;
        goto err;
    }

    /*
     * Calculate W = inv(S) mod Q save W in u2
     */
    if ((BN_mod_inverse(u2, s, dsa->q, ctx)) == NULL)
        goto err;

    /* save M in u1 */
    if (dgst_len > (i >> 3))
        /*
         * if the digest length is greater than the size of q use the
         * BN_num_bits(dsa->q) leftmost bits of the digest, see fips 186-3,
         * 4.2
         */
        dgst_len = (i >> 3);
    if (BN_bin2bn(dgst, dgst_len, u1) == NULL)
        goto err;

    /* u1 = M * w mod q */
    if (!BN_mod_mul(u1, u1, u2, dsa->q, ctx))
        goto err;

    /* u2 = r * w mod q */
    if (!BN_mod_mul(u2, r, u2, dsa->q, ctx))
        goto err;

    if (dsa->flags & DSA_FLAG_CACHE_MONT_P) {
        mont = BN_MONT_CTX_set_locked(&dsa->method_mont_p,
                                      dsa->lock, dsa->p, ctx);
        if (!mont)
            goto err;
    }

    if (dsa->meth->dsa_mod_exp != NULL) {
        if (!dsa->meth->dsa_mod_exp(dsa, t1, dsa->g, u1, dsa->pub_key, u2,
                                    dsa->p, ctx, mont))
            goto err;
    } else {
        if (!BN_mod_exp2_mont(t1, dsa->g, u1, dsa->pub_key, u2, dsa->p, ctx,
                              mont))
            goto err;
    }

    /* let u1 = u1 mod q */
    if (!BN_mod(u1, t1, dsa->q, ctx))
        goto err;

    /*
     * V is now in u1.  If the signature is correct, it will be equal to R.
     */
    ret = (BN_ucmp(u1, r) == 0);

 err:
    if (ret < 0)
        DSAerr(DSA_F_DSA_DO_VERIFY, ERR_R_BN_LIB);
    BN_CTX_free(ctx);
    BN_free(u1);
    BN_free(u2);
    BN_free(t1);
    return (ret);
}

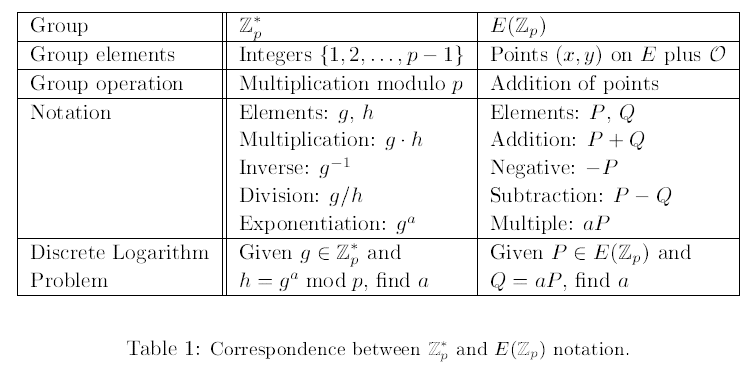
2、ECDSA