基本算法思想

常用算法思想概述

  在实际应用中，不同的问题往往解题的思路不同。如果找不到一个合适的思路，那么可能使求解决过程变得复杂，更有甚者无法求解得到结果。选择合理的思路，往往可以帮助用户理清问题的头绪，更快地解决问题。算法就是起到了这个作用。
  根据问题的不同，我们可以采用如下几种常用的算法来进行求解。

• 穷举算法思想
• 递推算法思想
• 递归算法思想
• 分治算法思想
• 概率算法思想

穷举算法思想

  穷举算法（Exhaustive Attack method）是最简单的一种算法，其依赖于计算机的强大计算能力，来穷尽每一种可能的情况，从而达到求解问题的目的。穷举算法效率并不高，但是适合于一些没有明显规律可循的场合。

基本思想

  穷举算法的基本思想就是从所有可能的情况中搜索正确的答案，其执行步骤如下：
  （1）对于一种可能的情况，计算其结果。
  （2）判断结果是否满足要求，如果不满足则继续执行（1）步来搜索下一个可能的情况；如果满足要求，则表示寻找到一个正确的答案。
  在使用穷举算法时，需要明确问题的答案的范围，这样才可以在指定范围内搜索答案，指定范围之后，就可以使用循环语句和条件判断语句逐步验证候选答案的正确性，从而得到需要的正确答案。

实例

  今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？
  这个问题的大致意思是：在一个笼子关着若干只鸡和若干只兔，从上面数共有35个头，从下面数共有94只脚，问笼中鸡和兔的数量各是多少？

java

public static void main(String[] args) {

        int head, foot;
        Scanner sc = new Scanner(System.in);
        System.out.println("穷举法求解鸡兔同笼问题");
        System.out.print("请输入头数： ");
        head = sc.nextInt();
        System.out.print("请输入脚数： ");
        foot = sc.nextInt();
        qiongju(head, foot);
    }

    private static void qiongju(int head, int foot) {
        int haveResult = 0;
        int chick, habbit = 0;
        for(chick = 0; chick <= head; chick++){
            habbit = head - chick; //鸭数目
            if(chick * 2 + habbit * 4 == foot){
                haveResult = 1; //判断，确定是否有答案
                break;
            }
        }
        if(haveResult == 1)
            System.out.println("鸡有" + chick + "只， 兔有" + habbit + "只");
        else
            System.out.println("无法求解！");
    }

运行结果

穷举法求解鸡兔同笼问题
请输入头数： 35
请输入脚数： 94
鸡有23只， 兔有12只

递推算法思想

  递推算法是很常用的算法思想，在数学计算等场合有着广泛的应用，递推算法适合有着明显公式规律的场合。

递推算法基本思想

  递推算法是一种理性思维模式的代表，其根据已有的数据和关系，逐步推导而得到结果。递推算法的执行过程如下：
  （1）根据已知结果和关系，求解中间结果。
  （2）判定是否达到要求，如果没有达到，则继续根据已知结果和关系求解中间结果；如果满足要求，则表示寻找到一个正确的答案。
递推算法往往需要用户知道答案和问题之间的逻辑关系。在许多数学问题中，都有着明确的计算公式可以遵循，因此往往可以采用递推算法来实现。

实例

  数学里面的斐波那契数列便是一个使用递推算法的经典例子。13世纪意大利数学家斐波那契的《算盘书》中记载了典型的兔子产仔问题，其大意如下：
  如果一对两个月大的兔子以后每一个月都可以生一对小兔子，而一对新生的兔子出生两个月后才可以生小兔子。也就是说，1月份出生，3月份才可产仔。那么假定一年内没有产生兔子死亡事件，那么1年后共有多少对兔子呢？

  分析，我们来逐月看一次每月的兔子对数：
第一个月：1对兔子；
第二个月：1对兔子；
第三个月：2对兔子；
第四个月：3对兔子；
第五个月：5对兔子；
……
  从上面可以看出，从第3个月开始，每个月的兔子总对数等于前两个月兔子数的总和。相应的计算公式如下：第n个月兔子总数Fn=Fn-2 + Fn-1

java

public static void main(String[] args) {
        int month, num; //月份数
        Scanner sc = new Scanner(System.in);
        System.out.print("请输入繁殖时间（月）：");
        month = sc.nextInt();
        num = Fabonacci(month); //斐波那契，求解
        System.out.printf("经过%d月的时间，共能繁殖成%d对兔子", month, num);
    }

    private static int Fabonacci(int month) { //递归调用 
        int t1, t2;
        if(month == 1 || month ==2) return 1;
        else{
            t1 = Fabonacci(month - 2);
            t2 = Fabonacci(month - 1);
            return t1 + t2;
        }
    }

运行结果：

请输入繁殖时间（月）：12
经过12月的时间，共能繁殖成144对兔子

递归算法思想

  递归算法是很常用的算法思想，使用递归算法，往往可以简化代码编写，提高程序的可读性，但是，有的不合适的递归往往导致程序的执行效率变低。

递归算法基本思想

  递归算法就是在程序中不断反复调用自身来达到求解问题的方法。这里的重点是调用自身，这就要求待求解的问题能够分解为相同问题的一个子问题。这样，通过多次递归调用，便可以完成求解。
  递归调用是一个方法在其方法体内调用其自身的方法调用方式。这种方法也称为“递归方法”。在递归方法中，主调方法又是被调方法。执行递归方法将反复调用其自身。每调用一次就进入新的一层。
  方法的递归调用分两种情况：直接递归和间接递归。

• 直接递归，即在方法中调用方法本身。
• 间接递归，即间接地调用一个方法，如func_a调用func_b，func_b调用func_a，间接递归用得不多。
    编写递归方法时，必须使用if语句强制方法在未执行递归调用前返回。如果不这样做，在调用方法后，它将永远不会返回，这是一个很容易犯的错误。

实例

  求n的阶乘：n! = n * (n-1) * (n-2) * ……* 2 * 1

java

public static void main(String[] args) {
        int n;
        long result; 
        Scanner sc = new Scanner(System.in);
        System.out.print("请输入要求阶乘的一个整数：");
        n = sc.nextInt();
        result = Fact(n); //阶乘方法，求解
        System.out.printf("%d的阶乘结果为%s", n, result);
    }

    private static long Fact(int n) {
        if( n <= 1) return 1;
        else return n * Fact(n-1);
    }

分治算法思想

  分治算法是一种化繁为简的算法思想。分治算法往往应用于计算步骤比较复杂的问题，通过将问题简化而逐步得到结果。

分治算法基本思想

  分治算法的基本思想是将一个计算复杂的问题分为规模较小，计算简单的小问题求解，然后综合各个小问题，而得到最终问题的答案，分治算法的执行过程如下：
  （1）对于一个规模为N的问题，若该问题可以容易地解决（比如说规模N较小），则直接解决；否则执行下面的步骤。
  （2）将该分解为M个规模较小的子问题，这些子问题互相独立，并且与原问题形式相同。
  （3）递归地解这些子问题
  （4）然后，将各子问题的解合并得到原问题的解。

实例

  通过一个例子来看分治算法的应用。一个袋子里有30个硬币，其中一枚是假币，并且假币和真币一模一样，肉眼很难分辨，目前只知道假币比真币重量轻一点，请问如何区分出假币呢？
1. 分治算法
  我们先来分析一下寻找假币问题，可以采用递归分治的思想来求解这个问题，操作步骤如下：
  （1）首先为每个银币编号，然后可以将所有的银币等分为两份，放在天平的两边。这样就将区分30个硬币的问题，变为区别两堆硬币的问题。
  （2）因为假银币的分量较轻，因此天平较轻的一侧中一定包含假银币。
  （3）再将较轻的一侧中的硬银币等分为两份，重复上述的做法。
  （4）直到剩下两枚硬银币，可用天平直接找出假币来。

java

public static void main(String[] args) {
        final int MAXNUM = 30; //银币总数
        int[] coin = new int[MAXNUM]; //银币数组
        initialization(coin); //数组初始化，设置其中一枚为假的
        int index = FalseCoin(coin, 0, coin.length - 1); //分治求解
        System.out.printf("在%d枚银币中，第%d枚是假的", coin.length, index);
    }

    //分治求解
    private static int FalseCoin(int[] coin, int low, int high) {
        int sum1, sum2;//sum1是前半段和，sum2是后半段和
        int index; //假币位置
        sum1 = sum2 = 0;
        if(low + 1 == high) //剩两枚
        {
            if(coin[low] < coin[high]) return low + 1;
            else return high + 1;
        }
        if((high - low + 1) % 2 == 0){ //剩偶数枚银币

            for(int k = low; k <= low + (high - low)/2; k++) //前半段和
                sum1 = sum1 + coin[k];
            for(int k = low + (high - low)/2 + 1; k <= high; k++) //后半段和
                sum2 = sum2 + coin[k];
            if(sum1 > sum2) return FalseCoin(coin, low + (high - low)/2 + 1, high);
            else return FalseCoin(coin, low, low + (high - low)/2);

        }else{  //剩奇数枚银币

            for(int k = low; k <= low + (high - low)/2 - 1; k++) //前半段和
                sum1 = sum1 + coin[k];
            for(int k = low + (high - low)/2 + 1; k <= high; k++) //后半段和
                sum2 = sum2 + coin[k];
            if(sum1 > sum2) return FalseCoin(coin, low + (high - low)/2 + 1, high);
            else{
                if(sum2 > sum1)
                    return FalseCoin(coin, low, low + (high - low)/2 - 1);
                else
                    return low + (high - low)/2 + 1;
            }
        }
    }

    //数组初始化，设置其中一枚为假的
    private static void initialization(int[] coin) {
        for(int i = 0; i < coin.length; i++)
            coin[i] = 2;
        int index = (int)(Math.random() * (coin.length));
        coin[index] = 1;
    }

运行结果

在30枚银币中，第2枚是假的

概率算法思想

  概率算法依照概率统计的思路来求解问题，其往往不能得到问题的精确解，但是在数值计算领域得到了广泛的应用。因为很多数学问题，往往没有或者很难计算，这时候便需要通过数值计算来求解近似值。

概率算法基本思想

  概率算法执行的基本过程如下：
  （1）将问题转化为相应的几何图形S，S的面积是容易计算的，问题的结果往往对应几何图形中某一部分S1的面积。
  （2）然后，向几何图形中随机撒点。
  （3）统计几何图形S中和S1中的点数。根据S的面积和S1面积的关系以及各图形中的点数来计算得到结果。
  （4）判断上述结果是否在需要的精度之内，如果未达到精度则进行执行步骤（2），如果达到精度，则输出近似结果。

  概率算法大致分为如下4种形式

• 数值概率算法
• 蒙特卡罗（Monte Carlo）算法
• 拉斯维加斯（Las Vegas）算法
• 舍伍德（Sherwood）算法

实例

  通过一个实例来看看蒙特卡罗（Monte Carlo）概率算法的应用。蒙特卡罗算法的一个典型应用便是计算圆周率z。

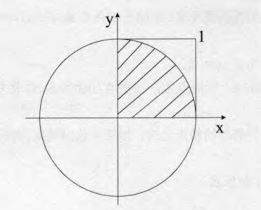
java

public static void main(String[] args) {
        System.out.println("蒙特卡罗概率算法计算∏");
        Scanner sc = new Scanner(System.in);
        System.out.print("输入点的数量：");
        int num = sc.nextInt();  //输入撒点个数
        double PI = MontePI(num); //计算PI
        System.out.println("PI=" + PI);
    }

    private static double MontePI(int num) {
        double x, y;
        int sum = 0;
        for(int i = 0; i < num; i++){
            x = Math.random(); //产生0~1之间的一个随机数
            y = Math.random(); //产生0~1之间的一个随机数
            if((x * x + y * y) <= 1) //计数，落在阴影中的点数
                sum ++; 
        }
        return (double)(4 * sum) / num;
    }

运行结果

蒙特卡罗概率算法计算∏
输入点的数量：50000000
PI=3.1418696