漫步线性代数十六——投影和最小二乘

目前为止，我们已经知道$Ax=b$要么有解要么无解，如果$b$ 不在列空间$C(A)$ 里，那么这个系统就是矛盾的，高斯消元法就会失败。当有几个方程和一个未知量时失败完全可以确定：

$$\begin{array}{ccc} 2x&=&b_1\\3x&=&b_2\\4x&=&b_3 \end{array}$$

当$b_1,b_2,b_3$的比率是$2:3:4$时，上面的方程组才可解，也就是说只有$b$ 和列$a=(2,3,4)$在一条直线上时$x$才会存在。

尽管他们无解，可是他们在实际中经常出现，他们必须有解！一种可能是用系统的一部分来确定$x$，其余部分忽略；如果所有的$m$个方程来源一样，这种方法就不合理。我们放弃这种一些方程没误差，而有些误差大的想法，我们考虑能最小化$m$个方程平均误差$E$的$x$值。

对平方和求平均是最方便的：

$$E^2=(2x-b_1)^2+(3x-b_2)^2+(4x-b_3)^2$$

如果存在准确解，那么最小误差$E=0$。大部分情况下，$b$和$a$不成比例关系，$E^2$的图像将是一个抛物线，最小误差在最低点的位置处，也就是导数等于零的位置：

$$\frac{dE^2}{dx}=2[(2x-b_1)2+(3x-b_2)3+(4x-b_3)4]=0$$

求出$x$的值，这个模型系统$ax=b$的最小二乘解用$\hat{x}$ 来表示：

$$\hat{x}=\frac{2b_1+3b_3+4b_3}{2^2+3^2+4^2}=\frac{a^Tb}{a^Ta}$$

相信大家立马就认出分子中的$a^Tb$和分母中的$a^Ta$了吧(是不是像投影啊)。

推广到一般情况同样如此，求解$ax=b$就是最小化

$$E^2=\Vert ax-b\Vert^2=(a_1x-b_1)^2+\cdots+(a_mx-b_m)^2$$

对$E^2$求导并令其等于零，求出点$\hat{x}$

$$(a_1\hat{x}-b_1)a_1+\cdots+(a_m\hat{x}-b_m)a_m=0$$

计算后得到$\hat{x}=(a_1b_1+\cdots+a_mb_m)/(a_1^2+\cdots+a_m^2)$。

11、对于$ax=b$这样只有一个未知变量的问题，它的最小二乘解为：$\hat{x}=\frac{a^Tb}{a^Ta}$

大家可能看出来了，我们一直从几何角度解释最小二乘问题—— 最小化距离。令$E^2$的导数等于零求出解，求得的结果和上篇文章的几何形式一样，连接$b,p$ 的误差向量$e$一定垂直于$a$：

$$a^T(b-\hat{x}a)=a^Tb-\frac{a^Tb}{a^Ta}a^Ta=0$$

注意退化为$a=0$的情况，这是$a$的任何倍数都是零，线仅仅就是一个点，因此$p=0$是唯一的投影候选结果。但是$\hat{x}$的形式变成一个无意义的数$0/0$，这表明$\hat{x}$完全无法确定，所有$x$值都给出相同的误差$E=\Vert 0x-b\Vert$，所以$E^2$是一条水平线而不是抛物线，伪逆给这种情况分配了一个确定的值$\hat{x}=0$，相比较其他值，这个是最好的选择的。

最小二乘问题

现在我们开始难一点的问题，将$b$投影到一个子空间上——而不是一条线上。这个问题来自于$Ax=b$，其中$A$是$m\times n$矩阵，不再是一列和一个未知量$x$，现在矩阵有多列，$m$ 的个数比未知量$n$的个数要大，所以跟期望中的一样，$Ax=b$依然是矛盾的。不可能存在完全拟合数据$b$的$x$值，换句话说，向量$b$不是$A$列向量的组合；它在列空间的外面。

再次回到了找出$\hat{x}$来最小化误差的问题，这个最小化可以用最小二乘求解，误差是$E=\Vert Ax-b\Vert$，这就是$b$到列空间中$Ax$的距离。我们要做的就是能最小化$E$的最小二乘解$\hat{x}$，它和$p=A\hat{x}$相等，而这个$p$就是列空间中离$b$最近的点。

我们可以用几何或计算来确定$\hat{x}$，在$n$维空间中，我们偏爱几何；$p$ 一定是$b$在列空间上的投影。误差向量$e=b-A\hat{x}$一定可这个空间垂直(图1)，找到$\hat{x}$和投影$p=A\hat{x}$是最基本的，下面我们用两种方法来实现它：

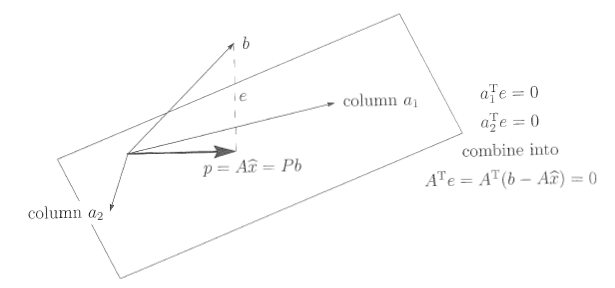
1. 所有垂直于列空间的向量位于左零空间里，因此误差向量$e=b-A\hat{x}$一定在$A^T$的零空间里： $$A^T(b-A\hat{x})=0\quad or\quad A^TA\hat{x}=A^Tb$$
2. 误差向量和$A$的每列$a_1,\ldots,a_n$垂直： $$\begin{matrix}a_1^T(b-A\hat{x})=0\\\vdots\\a_n^{T}(b-A\hat{x})=0\end{matrix}\quad or\quad \begin{bmatrix}a_1^T\\ \vdots\\a_n^T\end{bmatrix}\begin{bmatrix} \\b-A\hat{x}\\ \end{bmatrix}=0$$
   
   
   图1
   

这两种方法殊途同归，最后都是$A^T(b-A\hat{x})=0,A^TA\hat{x}=A^Tb$，而计算方法是通过计算$E^2=(Ax-b)^T(Ax-b)$的导数，并令其等于零得$2A^TAx-2A^Tb=0$，最快的方式是方程$Ax=b$两边乘以$A^T$，所有这些等价方法都得到一个二次系数矩阵$A^TA$，它是对称的(它的转置可不是$AA^T$!)并且是接下来几篇文章中非常基础的矩阵。

方程$A^TA\hat{x}=A^Tb$在统计学中叫做正规方程。

12、当$Ax=b$是矛盾的时候，它的最小二乘解就是最小化$\Vert Ax-b\Vert^2$：

ATAx^=ATb(1)

$$\begin{equation}A^TA\hat{x}=A^Tb\tag1\end{equation}$$ 当$A$的列线性无关时，$A^TA$是可逆的！因此
$$\begin{equation}\hat{x}=(A^TA)^{-1}A^Tb\tag2\end{equation}$$ $b$在列空间上的投影就是最近点$A\hat{x}$： $$\begin{equation}p=A\hat{x}=A(A^TA)^{-1}A^Tb \tag3\end{equation}$$

我们举一个例子进行说明：

$$A=\begin{bmatrix}1&2\\1&3\\0&0\end{bmatrix},\quad b=\begin{bmatrix}4\\5\\6\end{bmatrix}, Ax=b\text{没有解},A^TA\hat{x}=A^Tb\text{给出最佳解}x$$

每个列最后一个元素都是零，所以$C(A)$是三维空间中的$x-y$平面，$b=(4,5,6)$的投影是$p=(4,5,0)$，$x,y$分量保持不变，但$z$分量变成零，通过求解正规方程就能证实这个结果：

$$A^TA=\begin{bmatrix}1&1&0\\2&3&0\end{bmatrix}\begin{bmatrix}1&2\\1&3\\0&0\end{bmatrix} =\begin{bmatrix}2&5\\5&13\end{bmatrix}$$

$$\hat{x}=(A^TA)^{-1}A^Tb=\begin{bmatrix}13&-5\\-5&2\end{bmatrix}\begin{bmatrix}1&1&0\\2&3&0\end{bmatrix}\begin{bmatrix}4\\5\\6\end{bmatrix} =\begin{bmatrix}2\\1\end{bmatrix}$$

$$\text{投影：}p=A\hat{x}=\begin{bmatrix}1&2\\1&3\\0&0\end{bmatrix}\begin{bmatrix}2\\1\end{bmatrix} =\begin{bmatrix}4\\5\\0\end{bmatrix}$$

在这种特殊情况，最佳方式就是求解$Ax=b$的前两个方程，得到$\hat{x}_1=1,\hat{x}_2=1$，方程$0x_1+0x_2=6$的误差是6。

注解：假设$b$在$A$的列空间里，也就说存在列的组合使得$b=Ax$，那么$b$的投影依然是$b$：

$$p=A(A^TA)^{-1}A^TAx=Ax=b$$

最近的点$p$就是$b$本身。

注解：考虑一个极端的情况，假设$b$与每列都垂直，那么$A^Tb=0$，这种情况下$b$的投影就是零向量：

$$p=A(A^TA)^{-1}A^TAx=A(A^TA)^{-1}0=0$$

注解：当$A$是方阵且可逆时，列空间就是整个空间，每个向量的投影就是自身，$p=b,\hat{x}=x$：

$$p=A(A^TA)^{-1}A^TAx=AA^{-1}(A^T)^{-1}A^Tb=b$$

只有这一种情况我们可以将$(A^TA)^{-1}$分离成$A^{-1}(A^T)^{-1}$，当$A$是长方形矩阵时，就不能这么做。

注解：假设$A$只有一列，也就是只包含$a$，那么矩阵$A^TA$就是常数$a^Ta$，$\hat{x}$就是$a^Tb/a^Ta$，回到了最初的形式。

矩阵$A^TA$

矩阵$A^TA$一定是对称的，因为它的转置$(A^TA)^T=A^TA^{TT}$，依然是$A^TA$。它的第$i,j$($j,i$) 个元素是$A$的第$i$列与第$j$行的内积，重点是$A^TA$ 的可逆性，幸运的是$A^TA$与$A$有相同的零空间。如果$Ax=0$，那么$A^TAx=0$，$A$零空间中的向量$x$也在$A^TA$的零空间中。反过来考虑，假设$A^TAx=0$，我们将它和$x$进行内积操作来表明$Ax=0$：

$$x^TA^TAx=0,\quad or\quad \Vert Ax\Vert^2=0,\quad or\quad Ax=0$$

两个零空间是相等的。如果$A$有无关列(零空间中只有$x=0$)，那么$A^TA$同样如此：

13、如果$A$有无关列，那么$A^TA$是方阵，对称并且可逆。

随后我们还会指出$A^TA$也是正定的(所有主元和特征值都是正的)。

到目前为止，这种情况是最常见也是最终要的，如果$m>n$，那么$m$维空间的无关性就很容易实现。

投影矩阵

我们已经说明了离$b$的最近点是$p=A(A^TA)^{-1}A^Tb$，这种形式用矩阵形式来表示就是构建$b$到$A$列空间的垂线，产生$p$的矩阵是一个投影矩阵，用$P$ 表示：

$$\begin{equation} P=A(A^TA)^{-1}A^{T}\tag4 \end{equation}$$

这个矩阵将任何向量$b$投影到$A$的列空间上，换句话说，$p=Pb$是$b$在列空间上的分量，误差$e=b-Pb$是正交补中的分量。($I-P$也是一个投影矩阵！它将$b$投影到正交补上，投影是$b-Pb$)

简单来说，有一种矩阵形式可以将$b$分成两个互相垂直的分量，$Pb$在列空间$C(A)$内，其他的分量$(I-P)b$在左零空间$N(A^T)$内——也就是与列空间正交的空间。

这些投影矩阵可以从代数和几何两个角度理解。

14、投影矩阵$P=A(A^TA)^{-1}A^T$有两个性质：

- 矩阵等于自身的平方：$P^2=P$
- 矩阵等于它的转置：$P^T=P$

反过来讲，任何对称矩阵，如果$P^2=P$，那么它表示一种投影。

证明：很容易看出来为什么$P^2=P$，我们先从任意向量$b$开始，那么$Pb$位于投影的子空间内，当我们再次投影的话不会发生任何变化，向量$Pb$已经在子空间内，$P(Pb)$依然是$Pb$，换句话说$P^2=P$，两次或三次或五次投影得到的结果跟第一次一样：

$$P^2=A(A^TA)^{-1}A^TA(A^TA)^{-1}A^T=A(A^TA)^{-1}A^T=P$$

为了证明$P$是对称的，我们取它的转置：

$$P^T=(A^T)^T\left((A^TA)^{-1}\right)^TA^T=A(A^TA)^{-1}A^T=P$$

反过来，我们可以从$P^2=P,P^T=P$推断出$Pb$是$b$在$P$列空间上的投影，误差向量$b-Pb$与这个空间正交。对于该空间内的所有向量$Pc$，内积是零：

$$(b-Pb)^TPc=b^T(I-P)^TPc=b^T(P-P^2)c=0$$

因此$b-Pb$和空间是正交的，$Pb$是列空上的投影。

例1：假设$A$是可逆的，如果它是$4\times 4$矩阵，那么它的四列都是无关的，列空间就是整个$R^4$。在整个空间上的投影是什么？答案就是单位矩阵。

$$\begin{equation} P=A(A^TA)^{-1}A^T=AA^{-1}(A^T)^{-1}A^T=I\tag5 \end{equation}$$

单位矩阵是对称的，并且$I^2=I$，误差向量$b-Ib$等于零。

拟合数据的最小二乘法

假设我们有一堆实验数据，并且期望输出$b$是输入$t$的线性函数，也就是看成直线$b=C+Dt$，例如：

1. 我们测量不同时刻卫星距火星的距离，我们用$t$表示时间，$b$表示时间，不考虑失去动力或重力突然增强的情况下，卫星几乎以恒定的速度$v$移动：$b=b_0+vt$。
2. 我们在某个物体上放上不同的载荷，并测量它垂直方向产生的位移，我们用$t$ 表示载荷的重量，$b$表示位移大小。除非载太重使得物体彻底变形，否则的话根据弹性理论，存在一个线性关系$b=C+Dt$。
3. 印制$t$本书的成本似乎也是线性关系：$b=C+Dt$，其中编辑和排版成本是$C$，印刷和装订成本是$D$，$C$是固定的，而每印制一本书成本多$D$。

如何计算$C,D$呢？如果没有实验误差，那么两次测量的$b$都会得到直线$b=C+Dt$，但是如果有误差的话，我们就考虑平均值，求出最佳的直线。事实上，因为有两个未知量$C,D$需要确定，于是我们需要投影到二维子空间上。而一般情况下，我们都是多次进行试验测量的：

$$\begin{equation} \begin{array}{ccccc} C&+&Dt_1&=&b_1\\ C&+&Dt_2&=&b_2\\ &&\vdots&&\\ C&+&Dt_m&=&b_m\\ \end{array}\tag6 \end{equation}$$

得到的是矛盾方程组，有$m$个方程却只有两个未知量，如果误差存在的话，它将不可解。我们写成矩阵形式：

$$\begin{equation} \begin{bmatrix} 1&t_1\\ 1&t_2\\ \vdots&\vdots\\ 1&t_m\\ \end{bmatrix} \begin{bmatrix} C\\D \end{bmatrix}= \begin{bmatrix} b_1\\b_2\\\vdots\\b_m \end{bmatrix},\quad or\quad Ax=b\tag7 \end{equation}$$

最佳解$(\hat{C},\hat{D})$就是最小化均方误差$E^2$得到的$\hat{x}$：

$$E^2=\Vert b-Ax\Vert^2=(b_1-C-Dt_1)^2+\cdots+(b_m-C-Dt_m)^2$$

向量$p=A\hat{x}$是最接近向量$b$的，在所有的直线$b=C+Dt$中，我们选出拟合数据最好的直线(图2)，在图中，误差是到直线的竖直距离$b-C-Dt$(不是垂直距离!)，它对应的是竖直距离的平方，求和和最小化。

例2：在图2a中有三个测量值$b_1,b_2,b_3$：

$$t=-1,b=1;\quad t=1,b=1;\quad t=2,b=3$$

注意$t=-1,1,2$不要求等距离。第一步是通过三个点的方程：

$$Ax=b\quad is\quad \begin{array}{ccccc} C&-&D&=&1\\ C&+&D&=&1\\ C&-&2D&=&3 \end{array} \text{或者} \begin{bmatrix} 1&-1\\1&1\\1&2 \end{bmatrix} \begin{bmatrix} C\\D \end{bmatrix}= \begin{bmatrix} 1\\1\\3 \end{bmatrix}$$

如果这些方程$Ax=b$可解，那么表示没有误差。但是这些点不在一条直线上，所以他们不可解，因此需要用到最小二乘求解：

$$A^TA\hat{x}=A^Tb\text{得到} \begin{bmatrix} 3&2\\2&6 \end{bmatrix} \begin{bmatrix} \hat{C}\\\hat{D} \end{bmatrix}= \begin{bmatrix} 5\\6 \end{bmatrix}$$

最佳解就是$\hat{C}=\frac{9}{7},\hat{D}=\frac{4}{7}$，最佳直线是$\frac{9}{7}+\frac{4}{7}t$。

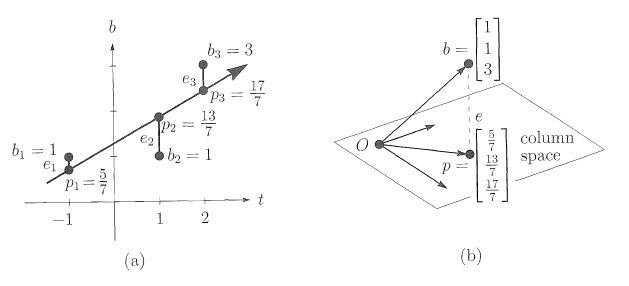
图2

注意这两幅图之间的联系，问题是一样的但是呈现的效果不一样。在图2b中，$b$不是列$(1,1,1),(-1,1,2)$的一个组合，而在图2a中，三个点不在一条线上。最小二乘用点$p$代替了不在直线上的点$b$！既然无法解$Ax=b$，那我们就解$A\hat{x}=p$。

直线$\frac{9}{7}+\frac{4}{7}t$在$-1,1,2$处的高度分别为$\frac{5}{7},\frac{13}{7},\frac{17}{7}$，这些点都在之直线上，因此向量$p=(\frac{5}{7},\frac{13}{7},\frac{17}{7})$在列空间里，而这个向量就是投影。图2b展示的是三维空间效果(如果有$m$个点就是$m$维)而图2a 是二维空间的效果(如果有$n$ 个参数就是$n$维)。

从$b$中减去$p$得到误差$e=(\frac{2}{7},-\frac{6}{7},\frac{4}{7})$，在图2a中就是竖直向量，他们是图2b中虚线向量的元素，这个误差向量与第一列$(1,1,1)$正交，因为$-\frac{2}{7}+\frac{6}{7}+\frac{4}{7}=0$，跟第二列也正交，所以它与列空间正交，属于左零空间。

问题：如果测量结果$b=(\frac{2}{7},-\frac{6}{7},\frac{4}{7})$就是误差，那么最佳直线和解$\hat{x}$是什么呢？答案是：零，也就是水平轴，$\hat{x=0}$，投影是零。

我们总结一下拟合直线的方法，$A$的第一列包含1，第二列包含$t$，因此$A^TA$包含$1,t,t^2$的和：

15、给定点$t_1,\cdots,t_m$处的测量值$b_1,\cdots,b_m$，那么最小二乘求$E^2$得到的直线$\hat{C}+\hat{D}t$为：

$$A^TA \begin{bmatrix} \hat{D}\\ \hat{D} \end{bmatrix} =A^Tb\text{或者} \begin{bmatrix} m&\Sigma t_i\\ \Sigma t_i&\Sigma t_i^2 \end{bmatrix} \begin{bmatrix} \hat{C}\\ \hat{D} \end{bmatrix}= \begin{bmatrix} \Sigma b_i\\ \Sigma t_ib_i \end{bmatrix}$$

注解：最小二乘法不限于用直线拟合数据，在许多实验中关系不一定是线性的。假设我们有一些放射性材料，在不同时刻$t$可以通过仪器读出放射量$b$。现在我们知道这些材料是两种化学物质的混合物，还知道他们的半衰期(或衰减率)，但是不知道每种的含量。如果我们用$C,D$ 表示这两个未知量，那么仪器的结果更像是两个指数之和(不是直线)：

$$\begin{equation} b=Ce^{-\lambda t}+De^{-\mu t}\tag8 \end{equation}$$

而实际测量中，仪器的结果存在误差，所以我们多测几次，分别在$t_1,\ldots,t_m$时刻测得$b_1,\ldots,b_m$，利用方程(8)近似满足：

$$Ax=b \text{就是} \begin{array}{ccccc} Ce^{-\lambda t_1}&+&De^{-\mu t_1}&\approx&b_1\\ &&\vdots&&\\ Ce^{-\lambda t_m}&+&De^{-\mu t_m}&\approx&b_m \end{array}$$

如果记录的次数超过两次$m>2$，那么我们可能无法求解，但是最小二乘原则将给出最佳解$\hat{C},\hat{D}$。

知道了$C,D$后情况就完全不同了，接下来我们就能算出衰减率$\lambda,\mu$。这个问题就是非线性最小二乘，比线性的难一点。而我们依然是先写出$E^2$，误差的平方和，然后最小化。但是导数为零得到的不再是线性方程。

加权最小二乘

一个简单的最小二乘问题是估计两个观测值$x=b_1,x=b_2$的$\hat{x}$，除非$b_1=b_2$，否则我们面对的就是两个方程一个未知量的矛盾方程：

$$\begin{bmatrix} 1\\1 \end{bmatrix} \begin{bmatrix} x \end{bmatrix}= \begin{bmatrix} b_1\\b_2 \end{bmatrix}$$

目前为止，我们认为$b_1,b_2$可靠度一样，基于此我们最小化$E^2$求出$\hat{x}$的值：

$$\frac{dE^2}{dx}=0\quad \hat{x}=\frac{b_1+b_2}{2}$$

最佳解就是平均值，利用$A^TA\hat{x}=A^Tb$得到同样的结果。事实上，$A^TA$是$1\times 1$的矩阵，正规方程是$2\hat{x}=b_1+b_2$。

现在假设两个观测值的信任程度不一样，$x=b_1$的结果比$x=b_2$更加准确，但不管怎样，只要$b_2$包含了信息，我们不会完全依赖$b_1$，最简单的分解就是给他们分配不同的权值$w_1^2,w_2^2$，最下化带权重的平方和：

$$E^2=w_1^2(x-b_1)^2+w_2^2(x-b_2)^2$$

如果$w_1>w_2$，那么说明$b_1$更加重要，最小化过程时会使$(x-b_1)^2$变小的力度加大：

$$\begin{equation} \frac{dE^2}{dx}=2[w_1^2(x_1-b_1)+w_2^2(x-b_2)]=0,\quad \hat{x}_W=\frac{w_1^2b_1+w_2^2b_2}{w_1^2+w_2^2}\tag9 \end{equation}$$

结果不再是$b_1,b_2$的平均值，而是数据的加权平均，这个平均相比$b_2$更加靠近$b_1$。

一般最小二乘问题将$Ax=b$变成新系统$WAx=Wb$，这将结果$\hat{x}$变成了$\hat{x}_W$，矩阵$W^TW$出现在正规方程的两边：

$WAx=Wb$的最小二乘解是$\hat{x}_W$：

$$\text{加权的正规方程}\quad (A^TW^TWA)\hat{x}_W=A^TW^TWb$$

在$b$投影到$A\hat{x}$的图像中发生了什么了？投影$A\hat{x}_W$依然是列空间中最靠近$b$的点，但是这里的最靠近有了新的意义，$x$的加权长度等于$Wx$的长度，垂直也不再是$y^Tx=0$，在新的方程组中是$(Wy)^T(Wx)=0$，中间出现了矩阵$W^TW$，在这个新观念下，投影$A\hat{x}_W$和误差$b-A\hat{x}_W$依然是垂直的。

接下里我们描述一下内积：他们来自于逆矩阵$W$。他们只涉及对称组合$C=W^TW$，$x,y$的内积是$y^TCx$。对于正交矩阵$W=Q$，当这个组合是$C=Q^TQ=I$时，这和我们之前介绍的内积是一个含义，这种情况下旋转空间不改变内积，而其他矩阵会改变长度和内积。

对任何可逆矩阵$W$，这些规则定义了新的内积和长度：

$$\begin{equation} (x,y)_W=(Wy)^T(Wx)\quad \Vert x\Vert_W=\Vert Wx\Vert\tag{10} \end{equation}$$

因为$W$是可逆的，所以没有任何向量会变成零(除了零向量)，所有可能的内积(线性依赖于$x,y$，并且在$x=y\neq 0$ 时为正)可以从$C=W^TW$ 中找到。

实际中，重要的问题是$C$的选择，最好的答案来自统计学，最早是出自高斯。我们知道平均误差是零，这是$b$中误差的期望值(误差并非一定为零!)，我们还知道误差平方的均值，也就是方差。如果$b_i$的误差互相独立，且方差为$\sigma_i^2$，那么正确的权值是$w_i=1/\sigma_i$，测量越精确(意味着更小的方差)，权重越大。

除了不同的权重外，观测量也许是不独立的，如果误差是耦合的，那么$W$将是非对角形式，最好的非偏置矩阵$C=W^TW$是协方差矩阵的逆(它的$i,j$项是$b_i$误差和$b_j$误差乘积的期望)，$C^{-1}$的主对角线包含方差$\sigma_i^2$，也就是$b_i$误差平方的平均值。

例3：假设两个牌友(已经叫牌了)在猜对方手中黑桃的个数，误差为$-1,0,1$的概率都等于$\frac{1}{3}$，那么期望误差是零，方差是$\frac{2}{3}$：

$$E(e)=\frac{1}{3}(-1)+\frac{1}{3}(0)+\frac{1}{3}(1)=0$$

$$E(e^2)=\frac{1}{3}(-1)^2+\frac{1}{3}(0)^2+\frac{1}{3}(1)^2=\frac{2}{3}$$

这两个人的猜测是相关的，因为叫牌是一样的，但是却不一样，这又是因为他们手中的牌不一样。如果说他们都猜大和都猜小的几率为零，相反误差的几率是$\frac{}1{3}$，那么$E(e_1e_2)=\frac{1}{3}(-1)$，协方差矩阵的逆是$W^TW$：

$$\begin{bmatrix} E(e_1^2)&E(e_1^2e_2)\\ E(e_1^2e_2)&E(e_2^2) \end{bmatrix}^{-1}= \begin{bmatrix} \frac{2}{3}&-\frac{1}{3}\\ -\frac{1}{3}&\frac{2}{3} \end{bmatrix}^{-1}= \begin{bmatrix} 2&1\\ 1&2 \end{bmatrix}^{-1} =C=W^TW$$

这就是加权正规方程中间的矩阵。