[机器学习] 2 K-近邻算法

该系列文章是依据本人平时对机器学习的学习，归纳总结，所做的学习笔记。如有错误或待改善之处，请留下您宝贵的意见或建议。

本节学习第一个机器学习算法：K-近邻算法，它非常有效且易于掌握。简单的说，K-近邻算法采用测量不同特征值之间的距离方法进行分类。

        

K-近邻算法的，优点：精度高，对异常值不敏感、无数据输入假定。

                       缺点：计算复杂度高、空间复杂度高。

                       适用数据范围：数值型和标称型。

 

K-近邻算法的工作原理：存在一个样本数据集合（也称作训练样本集合），并且样本集合中每个数据都存在标签，即我们知道样本集合中的每一个样本与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集合中的数据对应的特征进行比较，然后算法提取样本集合中特征最相似数据（最邻近）的分类标签。一般来说，我们只选取样本空间中的前K个最相似的数据，这就是K-近邻算法中K的出处，通常K是不大于20的整数。最后选择K个最相似数据中出现次数最多的分类，最为新数据的分类。

 

K-近邻算法的一般流程：

1.	收集数据：可以使用任何方法。
2.	准备数据：距离计算所需的数值，最好是结构化的数据结构。
3.	分析数据：可以使用任何方法。
4.	训练数据：此步骤不适合K-近邻算法。
5.	测试数据：计算错误率。
6.	使用算法：首先需要输入样本数据和结构化数据的输出结果，然后运行K-近邻算法判断输入数据分别属于哪个分类，最后应用对计算出的分类执行后续处理。

一、准备数据：使用Python的导入数据

创建KNN.py文件，在文件中增加如下代码：

1.	from numpy import *
2.	import operator
3.	
4.	def ceateDataSet():
5.		group = array([[11.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
6.		labels = ['A','A','B','B']
7.		return group,labels

在上面的代码中，我们导入了numpy和operator两个模块，其中numpy模块已在前一节中进行了相应的介绍，第二是运算模块。定义的函数ceateDataSet() 用于创建数据集合标签。

 

二、解析数据

定义函数classify分类数据。伪代码如下：

 

对未知类别属性的数据集中的每个点依次执行以下的操作：

1.	计算当前点与已知类别中的所有点的距离
2.	按距离的递增关系排序
3.	选取与当前点距离最小的K个点
4.	确定前K个点所在类别的出现频率
5.	返回出现频率最高的类别作为当前点的类别

classify函数的定义如下：

1.	def classify(item, dataset, labels, k):
2.	    dataset Size = dataSet.shape[0]
3.	    #计算距离
4.	    diffMat = tile(item, (dataSetSize,1)) - dataset
5.	    sqDiffMat = diffMat**2
6.	    sqDistances = sqDiffMat.sum(axis=1)
7.	    distances = sqDistances**0.5
8.	
9.	    sortedDistIndicies = distances.argsort()     
10.	    classCount={}      
11.	    #选择距离最小的K个点    
12.	    for i in range(k):
13.	        voteIlabel = labels[sortedDistIndicies[i]]
14.	        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
15.	
16.	    #排序
17.	    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
18.	    return sortedClassCount[0][0]

以上代码使用的是欧式距离：

   为了测试数据，在Python提示符中输入：

1.	>>>import KNN
2.	>>>Group,lables = KNN.createDataSet()
3.	>>>kNN.classify([0,0],group,lables,3)

三、使用K-近邻算法改进约会网站的配对效果

网站约会的人可分为3类：1. 不喜欢的人 2. 魅力一般的人 3. 极具魅力的人

代码及分析如下：

3.1 从文件中解析数据

1.	def file2matrix(filename):
2.	    fr = open(filename)
3.	    numberOfLines = len(fr.readlines())         #获得文件的行数
4.	    returnMat = zeros((numberOfLines,3))        #创建返回的NumPy矩阵
5.	    classLabelVector = []                       #创建返回的标识   
6.	    fr = open(filename)
7.	    index = 0
8.	    for line in fr.readlines():             # 解析文本数据到列表
9.	        line = line.strip()
10.	        listFromLine = line.split('\t')
11.	        returnMat[index,:] = listFromLine[0:3]
12.	        classLabelVector.append(int(listFromLine[-1]))
13.	        index += 1
14.	    return returnMat,classLabelVector

Python处理文本文件非常容易，首先需要知道文本文件包含多少行，打开文件获得行数。然后创建以零填充的NumPy矩阵。接着，使用函数line.strip()截取掉所有的回车符，然后使用tab字符\t将上一步得到的整行数据分割成一个元素列表，选择前3个元素将其存入特征矩阵中。使用索引值-1取最后一列元素存入向量classLabelVector中。需要注意的是，我们必须明确地通知解释器，告诉它列表中存储的元素值为整型，否则Python语言会将这些元素当作字符串处理。

3.2 归一化数值

1.	def autoNorm(dataSet):
2.	    minVals = dataSet.min(0)
3.	    maxVals = dataSet.max(0)
4.	    ranges = maxVals - minVals
5.	    normDataSet = zeros(shape(dataSet))
6.	    m = dataSet.shape[0]
7.	    normDataSet = dataSet - tile(minVals, (m,1))
8.	    normDataSet = normDataSet/tile(ranges, (m,1))   #element wise divide
9.	    return normDataSet, ranges, minVals

如果想要计算样本3和样本4之间的距离，可以使用下面的方法：

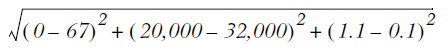
我们很容易发现，上面方程中数字差值最大的属性对计算结果的影响最大，也就是说，每年获取的飞行常客里程数对于计算结果的影响将远远大于其他两个特征---玩视频游戏的和每周消费冰洪淋公升数---的影响。而产生这种现象的唯一原因，仅仅是因为飞行常客里程数远大于其他特征值。但海伦认为这三种特征是同等重要的，因此作为三个等权重的特征之一，飞行常客里程数并不应该如此严重地影响到计算结果。

在处理这种不同取值范围的特征值时，我们通常采用的方法是将数值归一化，如将取值范围处理为0到1或者-1到1之间。下面的公式可以将任意取值范围的特征值转化为0到1区间内的值：

newvalue= {oldvalue - min) / (max-min)

其中min和max分别是数据集中的最小特征值和最大特征值。虽然改变数值取值范围增加了分类器的复杂度，但为了得到准确结果，我们必须这样做。我们需要在文件KNN.py中增加一个新函数autoNorm()该函数可以自动将数字特征值转化为0到1的区间。

3.3 验证分类器

1.	def datingClassTest():
2.	    hoRatio = 0.50      #hold out 10%
3.	    datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')       #load data setfrom file
4.	    normMat, ranges, minVals = autoNorm(datingDataMat)
5.	    m = normMat.shape[0]
6.	    numTestVecs = int(m*hoRatio)
7.	    errorCount = 0.0
8.	    for i in range(numTestVecs):
9.	        classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
10.	        print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])
11.	        if (classifierResult != datingLabels[i]): errorCount += 1.0
12.	    print "the total error rate is: %f" % (errorCount/float(numTestVecs))
13.	    print errorCount

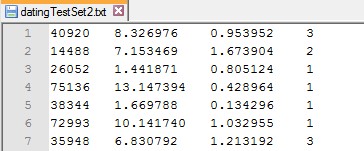
datingTestSet2.txt 中的部分数据如下：

该系列文章主要参考书目：<Machine Learning in Action>