堆排序

堆排序

    堆排序是利用堆的性质进行的一种选择排序。下面先讨论一下堆。

1.堆定义

  堆实际上是一棵完全二叉树，其任何一非叶节点满足性质：

  Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2]

  即任何一非叶节点的关键字大于等于或者小于等于其左右孩子节点的关键字。

  堆分为大顶堆和小顶堆，满足Key[i]>=Key[2i+1]&&key>=key[2i+2]称为大顶堆，满足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]称为小顶堆。由上述性质可知大顶堆的堆顶的关键字肯定是所有关键字中最大的，小顶堆的堆顶的关键字是所有关键字中最小的。

2.堆排序的主要思路：

1. 一般情况下都使用数组实现堆的结构，以大顶堆为例，因为是使用数组，元素下表从0开始，所以要求arry[i]>arry[i*2+1]，arry[i]>arry[i*2+2]。表示父结点大于其左右孩子结点的值。
2. 所以堆排序的第一步是根据其实数组元素，构建一个堆。构建堆就需要调整堆中的元素，从第一个非叶子结点开始调整，第一个非叶子结点的位置是t=(len/2-1)。因为堆是一棵满二叉树的结构，所以从0到t的所有结点都是非叶子结点。
3. 在调整堆结构过程中，我们需要比较父节点与其左右子结点的值，可以先求出左右子结点的最大值，即c=max(arry[leftChild],arry[rightChild])，然后将这个最大值与父节点arry[parent]进行比较，如果父节点小于子节点，那么交换父节点与子节点的值（子节点中较大的那个元素），如果父节点大与子节点，则表明满足堆结构要求，不需要交换。在调整的过程中可能会出现一种情况，比如父节点A与子节点B进行交换，此时A结点是B结点的子节点，但是A结点又是CD两个结点的父节点，因此我们还需要调整ACD三个元素位置，一直调整到结点没有子节点为止。
4. 在堆排序中，首先是构建一个最大堆，此处需要用到buildHeap(int arry[],int len)这个函数，而这个函数中又调用了adjustHeap(int arry[],int parent,int len)，所以可以将build看成是由adjustheap组成的。在构建完成以后，我们交换首元素与末元素的位置，交换以后我们知道首元素不符合最大堆的定义，所以需要调整首元素的位置，也就是adjustHeap(arry,0,len-i-1)。
5. 我们可以发现adjustHeap(int arry[],int parent,int len)的时间复杂读是o(logn)，而需要调用o(n)次这个方法啊，所以时间复杂度时o(nlogn)

  

3.操作过程如下：

    1)初始化堆：将R[1..n]构造为堆；

    2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

   因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

    下面举例说明：

    给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。

    首先根据该数组元素构建一个完全二叉树，得到

 

 然后需要构造初始堆，则从最后一个非叶节点开始调整，调整过程如下：

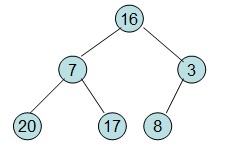
20和16交换后导致16不满足堆的性质，因此需重新调整

这样就得到了初始堆。

即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。

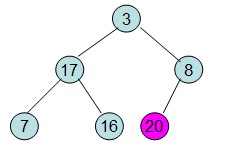此时3位于堆顶不满堆的性质，则需调整继续调整

 这样整个区间便已经有序了。

   从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序，不适合记录较少的排序。

4、时间复杂度分析

　　对深度为k的堆，“筛选”所需进行的关键字比较的次数至多为2(k-1); 
      对n个关键字，建成深度为的堆，所需进行的关键字比较的次数至多为4n; 
　　调整“堆顶”n-1次，总共进行的关键字比较的次数不超过
　　　　

　　　　
　　因此，堆排序的在最坏的情况下，时间复杂度为O(nlog2n)，这是堆的最大优点。堆排序方法在记录较少的情况下并不提倡，但对于记录较多的数据列表还是很有效的。因为其运行时间主要耗费在建初始堆和调整新建堆时的进行的返复筛选上。

  顾名思义，堆排序算法使用堆来排序无序的anarray数组。首先，算法将数组转换为堆。为完成转换，

    一种方法是使用heapInsert函数，将项逐一入堆。
    还有一种方法有数组anArray的项构建堆，这种方法的效率更高。假设anArray的原始内容如图1-a所示。将数组anArray的项指派给树的节点，从根开始，从左到右，逐渐下移将数组视为二叉树。结果如图1-b所示。此后，反复调用heapRebuilt，将该树转换为堆。heapRebuilt将半堆转换为堆。半堆的子树为堆，但根为就位。但是，树中有供heapRebuilt处理的半堆吗？图1-b的树不是半堆，但查看叶子，可以找到半堆；换言之，每个叶子是一个半堆。首先从左到右在叶子上调用heapRebuilt，接着沿树上移，在到达节点s时，其子树为堆。于是，heapRebuilt将以s为根的半堆转换为堆。

                                              
                     图1 （a）anArray的

                                                                             

   堆排序的效率分析与归并相似，在最坏的情况及平均情况下，两种算法均为O（n*log n）。与归并排序相比，堆排序的优势在于不需要第二个数组。快速排序在平均情况下也O（n*log n）,但在最坏的情况下为O（n^2）。尽管在最坏的情况下的效率不高，快速排序任然为首选的排序方法。

5.堆排序的c++实现

堆排序的主要思路：

1. 一般情况下都使用数组实现堆的结构，以大顶堆为例，因为是使用数组，元素下表从0开始，所以要求arry[i]>arry[i*2+1]，arry[i]>arry[i*2+2]。表示父结点大于其左右孩子结点的值。
2. 所以堆排序的第一步是根据其实数组元素，构建一个堆。构建堆就需要调整堆中的元素，从第一个非叶子结点开始调整，第一个非叶子结点的位置是t=(len/2-1)。因为堆是一棵满二叉树的结构，所以从0到t的所有结点都是非叶子结点。
3. 在调整堆结构过程中，我们需要比较父节点与其左右子结点的值，可以先求出左右子结点的最大值，即c=max(arry[leftChild],arry[rightChild])，然后将这个最大值与父节点arry[parent]进行比较，如果父节点小于子节点，那么交换父节点与子节点的值（子节点中较大的那个元素），如果父节点大与子节点，则表明满足堆结构要求，不需要交换。在调整的过程中可能会出现一种情况，比如父节点A与子节点B进行交换，此时A结点是B结点的子节点，但是A结点又是CD两个结点的父节点，因此我们还需要调整ACD三个元素位置，一直调整到结点没有子节点为止。
4. 在堆排序中，首先是构建一个最大堆，此处需要用到buildHeap(int arry[],int len)这个函数，而这个函数中又调用了adjustHeap(int arry[],int parent,int len)，所以可以将build看成是由adjustheap组成的。在构建完成以后，我们交换首元素与末元素的位置，交换以后我们知道首元素不符合最大堆的定义，所以需要调整首元素的位置，也就是adjustHeap(arry,0,len-i-1)。
5. 我们可以发现adjustHeap(int arry[],int parent,int len)的时间复杂读是o(logn)，而需要调用o(n)次这个方法啊，所以时间复杂度时o(nlogn)

#include<iostream>
using namespace std;

//函数声明
void PrintArry(int arry[], int len);//打印数组
void swap(int arry[], int i, int j);//交换数组元素
void AdjustHeap(int arry[], int parent, int len);//调整堆，使其满足堆的要求
void BuildHeap(int arry[], int len);//初始化堆
void HeapSort(int arry[], int len);//堆排序

void PrintArry(int arry[], int len)
{
  for (int i = 0; i<len; i++)
   cout << arry[i] << " ";
   cout << endl;
}

void swap(int arry[], int i, int j)
{
   int temp = arry[i];
   arry[i] = arry[j];
   arry[j] = temp;
}

void AdjustHeap(int arry[], int parent, int len)
{
    int c = parent * 2 + 1;//parent的左孩子结点，这里+1是因此头结点从0开始
    while (c<len)//如果左孩子小于堆长度
   {
      if (c + 1<len&&arry[c]<arry[c + 1])
        c++; //如果右孩子小于对长度并且右孩子大于左孩子，则获取右孩子的坐标
      if (arry[parent] >= arry[c])//如果父节点比孩子结点大则退出循环
       { break;
        }else{
         swap(arry, parent, c);//如果孩子结点比父节点大，则交换
         //因为孩子结点也可能是父结点，所以接下来继续调整孩子结点，直到父节点大于两个孩子结点或者没有孩子结点为止。
         parent = c;
         c = parent * 2 + 1;
      }
   }
}

//初始化堆
void BuildHeap(int arry[], int len)
{
    int begin = len / 2 - 1;//从第一个非叶子结点开始调整，直到最后的根结点，根结点是arry[0]
    for (int i = begin; i >= 0; i--)
    {
      AdjustHeap(arry, i, len);
   }
}

void HeapSort(int arry[], int len)
{
   //创建初始化堆，用数组实现堆的结构。
   BuildHeap(arry, len);
   //在初始化堆以后数组首元素arry[0]是最大的，交换首元素与堆的末尾元素，
   //这样就完成了对一个数排序，堆的长度-1
  for (int i = 0; i<len; i++)
  {
    swap(arry, 0, len - 1 - i);//交换堆顶元素与堆末尾元素
    AdjustHeap(arry, 0, len - 1 - i);//第一次交换后，继续调整整个长度为len-1的堆结构
                                     //len-1-i,代表调整堆的长度，不是数组下标，注意下。
   }
}

void main()
{
   int arry[] = { 1, 3, 6, 2, 7, 0, 8, 5 };
   int len = sizeof(arry) / sizeof(int);
   PrintArry(arry, len);

   HeapSort(arry, len);
   PrintArry(arry, len);
   system("pause");
}

因为堆是一种完全二叉树的结构所以我们可以用数组来存储。但是一般A[0]不存储元素，从A[1]开始
void BuildMaxHeap(ElemType A[] ,int len){
 for( int i=len/2; i>0; i++)
     AdjustDown(A,i,len);//从i=[len/2]~1反复调整堆；
}
void AdjustDown(ElenType A[],int k,int len){
     A[0]=A[i];//从第i个元素开始调整
    for(int  i=2*k; i<=len; i=2*i;）{//沿着Key较大的子节点向下筛选
       		if(i+1<=len&&a[i]<a[i+1]) { //或者i<len        
                    i++;                            //取key值较大的子节点的下标
       		  }
                  if(a[0]>=a[i])  break;   //比左右孩子节点都大则结束
                else{
                      a[k]=a[i];   //将A[i]调整到双亲节点上
                      k=i;        //修改k值，以便继续向下筛选
       		  }
       }
    A[k]=A[0];   //被筛选的节点放到最终位置上
}

堆排序（转载）

 堆排序与快速排序，归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。学习堆排序前，先讲解下什么是数据结构中的二叉堆。

二叉堆的定义

二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆：

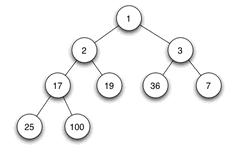
由于其它几种堆（二项式堆，斐波纳契堆等）用的较少，一般将二叉堆就简称为堆。

堆的存储

一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

堆的操作——插入删除

下面先给出《数据结构C++语言描述》中最小堆的建立插入删除的图解，再给出本人的实现代码，最好是先看明白图后再去看代码。

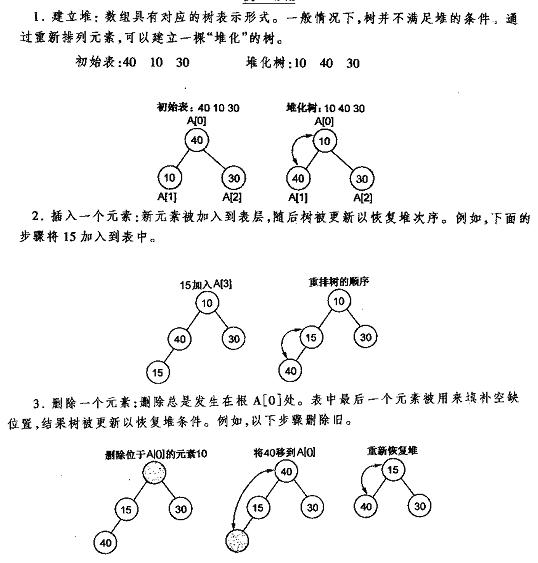
堆的插入

每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中，对照《白话经典算法系列之二 直接插入排序的三种实现》不难写出插入一个新数据时堆的调整代码：

[cpp] view plaincopy

1. //  新加入i结点  其父结点为(i - 1) / 2  
2. void MinHeapFixup(int a[], int i)  
3. {  
4.     int j, temp;  
5.       
6.     temp = a[i];  
7.     j = (i - 1) / 2;      //父结点  
8.     while (j >= 0 && i != 0)  
9.     {  
10.         if (a[j] <= temp)  
11.             break;  
12.           
13.         a[i] = a[j];     //把较大的子结点往下移动,替换它的子结点  
14.         i = j;  
15.         j = (i - 1) / 2;  
16.     }  
17.     a[i] = temp;  
18. }  

更简短的表达为：

[cpp] view plaincopy

1. void MinHeapFixup(int a[], int i)  
2. {  
3.     for (int j = (i - 1) / 2; (j >= 0 && i != 0)&& a[i] > a[j]; i = j, j = (i - 1) / 2)  
4.         Swap(a[i], a[j]);  
5. }  

插入时：

[cpp] view plaincopy

1. //在最小堆中加入新的数据nNum  
2. void MinHeapAddNumber(int a[], int n, int nNum)  
3. {  
4.     a[n] = nNum;  
5.     MinHeapFixup(a, n);  
6. }  

堆的删除

按定义，堆中每次都只能删除第0个数据。为了便于重建堆，实际的操作是将最后一个数据的值赋给根结点，然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的，如果父结点比这个最小的子结点还小说明不需要调整了，反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码：

[cpp] view plaincopy

1. //  从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2  
2. void MinHeapFixdown(int a[], int i, int n)  
3. {  
4.     int j, temp;  
5.   
6.     temp = a[i];  
7.     j = 2 * i + 1;  
8.     while (j < n)  
9.     {  
10.         if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的  
11.             j++;  
12.   
13.         if (a[j] >= temp)  
14.             break;  
15.   
16.         a[i] = a[j];     //把较小的子结点往上移动,替换它的父结点  
17.         i = j;  
18.         j = 2 * i + 1;  
19.     }  
20.     a[i] = temp;  
21. }  
22. //在最小堆中删除数  
23. void MinHeapDeleteNumber(int a[], int n)  
24. {  
25.     Swap(a[0], a[n - 1]);  
26.     MinHeapFixdown(a, 0, n - 1);  
27. }  

堆化数组

有了堆的插入和删除后，再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧，不用！先看一个数组，如下图：

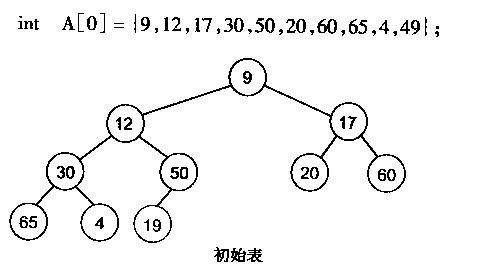
很明显，对叶子结点来说，可以认为它已经是一个合法的堆了即20，60， 65， 4， 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30，A[2] = 17，A[1] = 12，A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤：

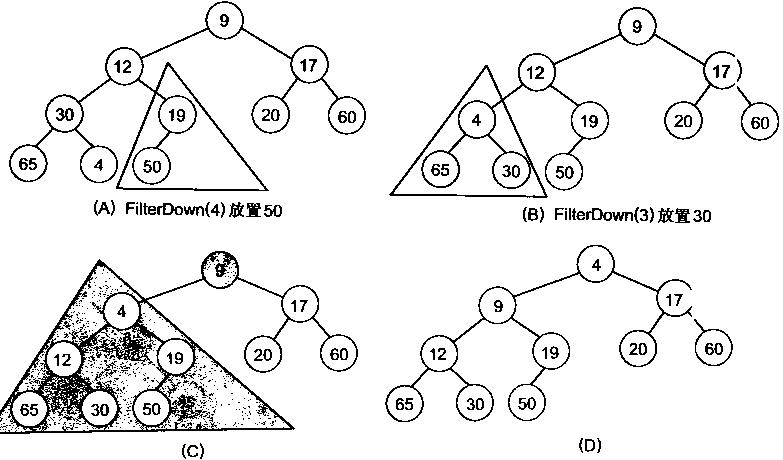
写出堆化数组的代码：

[cpp] view plaincopy

1. //建立最小堆  
2. void MakeMinHeap(int a[], int n)  
3. {  
4.     for (int i = n / 2 - 1; i >= 0; i--)  
5.         MinHeapFixdown(a, i, n);  
6. }  

至此，堆的操作就全部完成了(注1)，再来看下如何用堆这种数据结构来进行排序。

堆排序

首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据，重复上述步骤直至堆中只有一个数据时就直接取出这个数据。

由于堆也是用数组模拟的，故堆化数组后，第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换，再对A[0…n - 3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了。有点类似于直接选择排序。

[cpp] view plaincopy

1. void MinheapsortTodescendarray(int a[], int n)  
2. {  
3.     for (int i = n - 1; i >= 1; i--)  
4.     {  
5.         Swap(a[i], a[0]);  
6.         MinHeapFixdown(a, 0, i);  
7.     }  
8. }  

注意使用最小堆排序后是递减数组，要得到递增数组，可以使用最大堆。

由于每次重新恢复堆的时间复杂度为O(logN)，共N - 1次重新恢复堆操作，再加上前面建立堆时N / 2次向下调整，每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。STL也实现了堆的相关函数，可以参阅《STL系列之四 heap 堆》。

 

 

注1 作为一个数据结构，最好用类将其数据和方法封装起来，这样即便于操作，也便于理解。此外，除了堆排序要使用堆，另外还有很多场合可以使用堆来方便和高效的处理数据，以后会一一介绍。