poj3056The Bavarian Beer Party (不交差配对，区间DP)

Problem Description

The professors of the Bayerische Mathematiker Verein have their annual party in the local Biergarten. They are sitting at a round table each with his own pint of beer. As a ceremony each professor raises his pint and toasts one of the other guests in such a way that no arms cross.

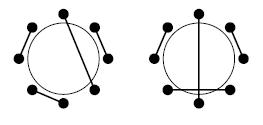
Figure 2: Toasting across a table with eight persons:no arms crossing(left), arms crossing(right)

We know that the professors like to toast with someone that is drinking the same brand of beer, and we like to maximize the number of pairs of professors toasting with the same brand , again without crossing arms. Write an algorithm to do this, keeping in mind that every professor should take part in the toasting.

Input

The frist line of the input contains a single number: the number of test cases to follow. Each test case has the following format:
One line with an even number p, satisfying 2 <= p <= 1000: the number of participants
One line with p integers (separated by single spaces) indicating the beer brands fro the consecutive professors( in clockwise order, starting at an arbitrary position). Each value is between 1 and 100 (boudaries included).

Output

For every test case in the input, the output should contain a single number on a single line: the maximum number of non-intersecting toasts of the same beer brand for this test case.

Sample Input

  
  

   
   2
6
1 2 2 1 3 3
22
1 7 1 2 4 2 4 9 1 1 9 4 5 9 4 5 6 9 2 1 2 9
  
  

Sample Output

  
  

   
   3
6
  
  

题意：有n个人围着卓，所有人都要成对敬酒，且不能有交差的，求最多有多少对成对敬酒。

题解：要所有可能成对且不交差，那么区间内一定是偶数个人。

#include<stdio.h>
#include<string.h>
int dp[2005][2005];
int max(int a,int b)
{
    return a>b?a:b;
}
int main()
{
    int t,n,ans[2005];
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&ans[i]);
        }
        for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        dp[i][j]=0;
        for(int r=1;r<n;r+=2)//保证区间人数为偶数，只有是偶数才能所有人成对敬酒
        for(int i=1;i<=n-r;i++)
        {
            int j=i+r;
            dp[i][j]=dp[i+1][j-1];//如果在区间内没有与i成对时
            for(int k=i+1;k<=j;k+=2)//保持小区间也成偶数
            if(ans[i]==ans[k])
                dp[i][j]=max(dp[i][j],dp[i+1][k-1]+1+dp[k+1][j]);
            else 
                dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]);
        }
        printf("%d\n",dp[1][n]);
    }
}